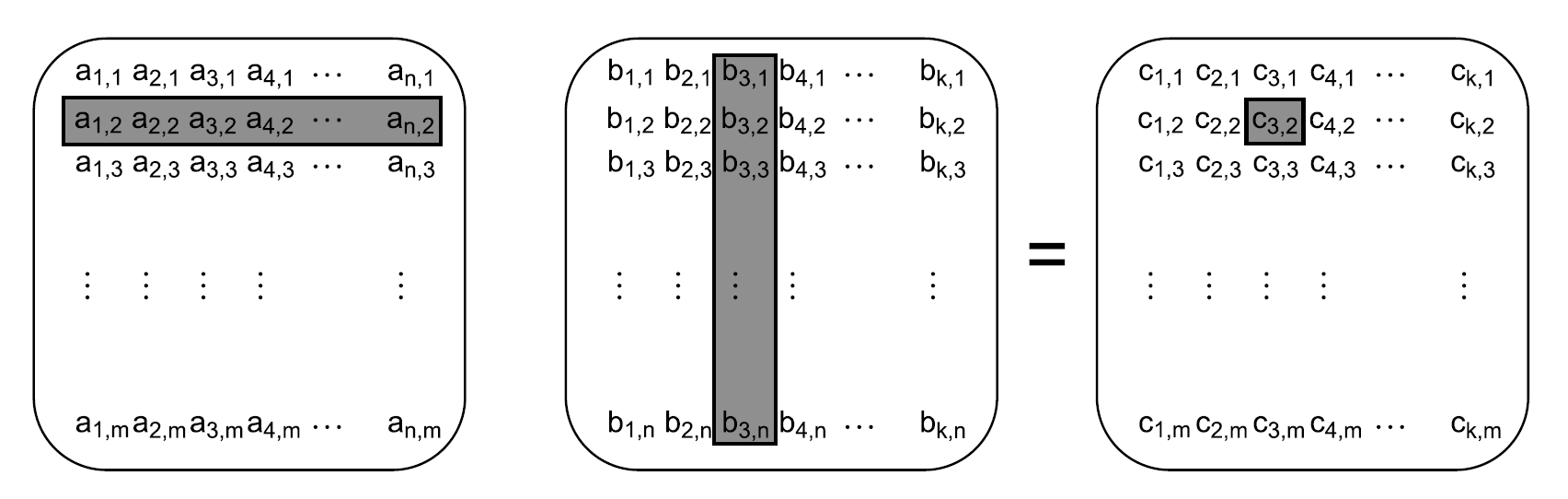
4.3 网络层-路由算法
网络层-选路算法
1 路由概述
网络中的主机通常都直接与一台路由器相连接,该路由器即为该主机的默认路由器,它是该主机的第一跳路由器。
每当主机发送一个分组时,它都首先将分组发送给起默认路由器,在接收端,目的主机的默认路由器把来自于网络上其它主机的分组转发给目的主机,因而网络中从源主机到目的主机的选路就是从源主机的默认路由器(也可以成为源路由器)到目的主机的默认路由器(也可以成为目的路由器)之间的选路问题。
选路算法的目的
给定一组路由器以及连接路由器的链路,选路算法要找到一条从源路由器到目的路由器之间的“好”路径。通常好路径指的是最低费用的路径。由于网络中的路由器组成的拓扑是典型的图结构,因而可以用图来研究选路问题。
在网络图中,节点表示路由器,边表示路由器之间的链路。给边赋予一个表示费用的值(费用可以为链路速度,金钱,线路长度等等),然后选路算法的目的就变为在图中找到给定的两点之间的具有最低费用的路径。
选路算法的分类
根据选路算法是全局的还是局部的,选路算法可以分为:
- 全局选路算法:用完整的,全局性的网络信息来计算从源到目的的最低费用路径。这种算法通常称为链路状态算法即LS算法,因为该算法必须知道网络中每条链路的费用。
- 分布式选路算法:以迭代的、分布式的方式计算出最低费用路径。没有节点拥有关于所有网络链路费用的完整信息,而每个节点仅有与其直接相连链路的费用信息即可开始工作。然后通过迭代计算过程并与相邻节点交换信息,一个节点逐渐计算出到达目的节点或者一组目的节点的最低费用路径。
根据算法是静态的还是动态的来分类:
- 静态选路算法:随着时间的推移,路由的变化非常缓慢,同时是在人的干预下进行调整。
- 动态选路算法:能够在网络流量负载或者拓扑发生变化时改变选路路径。动态选路算法可以周期性的运行或者在拓扑或链路费用发生变化时直接运行。
根据算法是负载敏感的还是负载迟钝的进行划分:
- 负载敏感算法:链路费用会动态的变化以反映底层链路的当前拥塞水平。
- 负载迟钝算法:当前的因特网选路算法(RIP、OSPF、BGP)都是负载迟钝的。
2 链路状态选路算法(LS)
LS算法原理
链路状态算法需要网络拓扑和所有链路费用信息作为输入。通过让所有节点都向网络中的所有其它路由器广播链路状态分组来完成。
每个链路状态分组包含了它所连接的链路的特征和费用。广播的结果是所有节点都具有了该网络的同一个完整的视图。于是每个节点都可以运行LS算法从而计算出相同的最低费用路径集合。
根据图论的知识,可以使用Dijkstra算法来计算最短路径。Prim算法也可以用于计算图中两个节点之间的最短路径,它适用于具有稀疏边的图。算法的复杂度为O(n2)。
3 距离向量选路算法(DV)
DV算法概述
距离向量算法DV(Distance-vector)是一种迭代的、异步的和分布的算法:
- 分布式的:每个节点都要从一个或多个直接相连的邻居收集某些信息,执行计算,然后将结果发回个邻居。
- 迭代的:该过程要一直持续到邻居之间没有更多的信息要交换为止。
- 异步的:各个节点的操作不需要保持一致。
DV算法原理
DV算法,利用了Bellman-Ford方程。
其中dx(y)表示从节点x到节点y的最低费用路径的费用。c(x,v)的含义是节点x到其邻居v的路径费用。方程式的含义是从节点x到节点y的最低费用路径的费用等于所有邻居v中c(x,v)+dv(y)最小的那个。
$$
d_x(y)=min_v{c(x,v)+d_v(y)}
$$在DV算法中,得到最小值的那个v节点就是当前节点向y转发时的下一跳节点,当需要向y转发时,只需要将分组送给节点v即可。算法思想:对于网络N中的素有节点,令Dx=[Dx(y):y属于N]是节点x的距离向量,该向量是从x到N中所有其它节点y的费用估计向量。每个节点x维护下列选路数据:
- 对于每个邻居v,从x到直接相连的邻居v的费用为c(x,v)。
- 节点x的距离向量,它包含了x到N中所有目的地的费用的估计值
- 它的每个邻居的距离向量,即对x的每个邻居v有Dv=[Dv(y):y属于N]
DV算法中,每个节点不时的向它的每个邻居发送它的距离向量的拷贝。当节点x收到他的邻居v的一个新的距离向量时,它保存v的距离向量,然后根据Bellman-Ford方程更新自己的距离向量。如果节点x的距离向量因这个更新而改变,则节点x将向它的每个邻居发送它的更新后的距离向量。 从邻居接收更新距离向量,重新计算选路表项和通知邻居到目的地的最低费用路径的费用已经变化的过程会一直持续知道无更新报文发送为止。DV算法被用于因特网的RIP和BGP。
DV算法过程
- 距离向量算法:链路费用变化和链路故障
运行DV算法的节点在检测到其到邻居的链路费用发生变化时就会更新器距离向量,并且如果最低费用路径发生了变化,它就向邻居通知其新的距离向量。当链路费用降低时,DV算法可以就得到变化后的最低费用。但是如果是链路费用增加,则会出现一点问题,如下图所示拓扑:

链路费用变化前,网络拓扑如上图所示,则Dy(x)=4,Dy(z)=1, Dz(y)=1, Dz(x)=5,在t0时刻,y检测到链路费用变化(从4增加到40)。y会更新器最低费用路径,根据Bellman-Ford方程,其计算出来的值为6。但是观察这个时候的网络拓扑,显然这是不正确的。出现这个现象的原因是:y更新器距离向量时,利用了z通告给它的z的距离向量,Dz(x)=5,但是显然,Dz(x)是依赖于Dy(x)的,在Dy(x)变化后它显然是一个错误的值。更重要的是在这个时刻,会出现选路环路:为了到达x,y通过z选路,而z又选择通过y选路,这样的选路结果是分组无法到达目的地。
y计算出来了一个新的到x的最低费用,因而它在t1时刻将新的距离向量通告给z
z收到y的新的距离向量后更新其距离向量,它计算出来的新的Dz(x)=7
该过程一直循环,直到计算出来一个正确的值Dy(x)=40,Dz(x)=41
从上述过程可以看到使用DV算法时,坏消息传递的比较慢。而且上述过程只是一个链路的费用变高了,如果有多个链路的费用变高,则会遇到所谓的计数到无穷的问题。
- 距离向量算法:增加毒性逆转
毒性逆转可以解决上述特定的网络拓扑中的环路状况。其思想是:如果z通过y选路,则z在通告y时会告诉y它(z)到x的距离是无穷大。毒性逆转只能解决这种特殊环路的问题,如果环路涉及到3个或更多的节点,则它也无能为力
LS和DV算法比较
DV算法中,每个节点仅与它的直接邻居交换信息,但它为它的邻居提供了通过它到达网络中(它所知道的)所有其它节点的最低费用估计。LS算法中,每个节点与所有节点交换信息,但它仅仅告其它节点与它直接相连的链路的费用。
- 报文复杂性:LS算法要求每个节点都要知道网络中每条链路的费用,因而它需要发送O(|N||E|)个报文,而且无论何时一条链路的费用发生变化,都必须向所有节点发送新的链路费用。DV算法要求在每次迭代时,在两个直接邻居之间交换报文。当链路费用发生变化时,仅当新的费用导致与该链路相连的节点的最低费用发生了变化时,才会传播已改变的链路费用。
- 收敛速度:LS算法是一个O(n2)的算法,而DV算法收敛较慢,且在收敛时会遇到选路环路。
- 健壮性:由于LS算法中每个节点都独立的计算自己的路由,因而这在一定程度上提供了健壮性。而DV算法中一个节点的不正确信息则会扩散到整个网络。
4 层次选路
采用层次选路的原因:
规模:因特网由上亿台主机组成,如果不采用层次选路,则路由器需要存储选路信息会需要极大的内存,而且如果采用LS算法,则可以预期网络将淹没在LS广播中无法工作;如果采用DV算法,可以预期它根本就不会收敛。
管理自治:某些组织可能倾向于按自己的意愿管理自己的网络,对外隐藏自己的内部网络面貌。
自治系统AS
解决这两个问题采用的方法是将路由器组织到自制系统(AS)。
每个AS由一组通常在相同管理控制下的路由器组成,相同的AS内部的路由器都运行同样的选路算法,且具有彼此之间的信息。在一个自制系统内运行的选路算法叫自制系统内部选路协议。AS内的一台或多台路由器将有另外的任务,即负责向本AS之外的目的地转发分组,这些路由器被称为网关路由器。
当AS只有一个网关路由器时,AS内的路由器很容易将目的地不属于本AS的分组转发到网关路由器(因为AS内的路由器都知道自己到达网关路由器的最短路径),然后由网关路由器转发到AS外部。
但是当AS有多个网关路由器时,AS就需要
- 知道经过与自己的网关路由器相连的其它AS可以到达哪些目的地
- 在本AS内部传播这些可达信息
这两项任务是由自治系统间选路协议完成的。因特网的所有AS都运行相同的自治系统间选路协议。每台路由器都接收来自一个AS内部的内部选路协议和一个AS间选路协议的信息,并使用这些信息配置自己的转发表。
当一个AS通过自治系统间选路协议知道它可以通过自己的多个网关路由器到达某个目的地时,AS内部的路由器如何添加自己到该目的的路由?通常采用的策略是热土豆选路(hot potato routing),其思想是让AS尽快摆脱分组,即尽快将分组转发给其它AS,路由器将选择具有下列特性的网关路由器,然后根据本路由器到该网关路由器的路径添加路由:
- 该网关路由器可以到达该目的地
- 该网关路由器到本路由器具有最低费用路径
当一个AS从一个相邻AS知道了一个目的地时,它可以向它的某些其它邻居AS通告该路由信息,但是是否通告,通告哪些内容是一个AS的管理策略问题。取决于AS的配置管理策略。
因此总结起来,在一个AS内部,所有路由器都运行相同的内部选路协议。在各AS之间,AS运行相同的自治系统间选路协议。AS内部的路由器仅需要知道本AS内部的路由器,AS的管理组织可以运行它选择的任何内部选路协议。