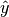区间估计

1 概述

定义1：置信区间

  • 声明
    $$
    总体分布族{P_\theta:\theta\in\Theta}\
    存在统计量T_1(x),T_2(x)，给定的\alpha(0<\alpha<1)
    $$
  • 条件
    $$
    P_\theta{T_1(x_1,\dotsm,x_n)\leq\theta\leq T_2(x_1,\dotsm,x_n)}\geq1-\alpha
    $$
  • 结论
    $$
    随机区间[T_1,T_2]为参数\theta的置信水平为1-\alpha的置信区间\
    T_1为置信下限，T_2为置信上限，1-\alpha为置信水平置信度
    $$

理解：置信度与置信区间的辩证关系

  • 置信度与置信区间之间存在不等式关系。置信度—随机变量区间的概率分布，之间存在不等式关系。可以通过其不等式关系+枢轴变量法，求得当前>=当前置信度$1-\alpha$的置信区间。
  • 在相同的置信区间下，置信度越高越好。在相同的置信度下，置信区间越小，表示精确度越高，越好。
  • 置信度表示可信程度，越高越好，置信区间表示精确度，越小越好。
  • 当样本容量n固定式，置信度越大，估计参数的可信度就越高，但置信区间也越大，同时会降低精确度。
  • 当置信区间越小，置信区间的精确度会提高，但置信度减小，可信度会变低。
  • 精确度和可信度是一对不可调和的矛盾。

2 枢轴变量法

t分布当自由度超过45之后可以看做N正太分布。

  1. 从参数$\theta$的一个具有优良性的点估计$\hat{\theta}$出发，构造包含$\theta$与$\hat{\theta}$的函数$g(\theta,\hat{\theta})$，使得g()的分布完全已知。
  2. 根据置信水平$1-\alpha$，选取两个常数a和b使得：
    $$
    P_\theta{a\leq g(\hat{\theta},\theta)\leq b}=1-\alpha
    $$
  3. 因为g的概率分布已知，g的不等式可解。将$\theta$作为未知数，求得最终的区间，用点估计值域其他参数计算得到。
    $$
    a\leq g(\hat{\theta},\theta)\leq b\
    \hat{\theta}_1\leq\theta\leq\hat{\theta}_2
    $$

注意事项

  1. 构造枢轴变量$g(\hat{\theta},\theta)$，使用熟悉的$N(0,1),\chi^2,t,F$等分布
  2. 对于常见分布，一半选取a为g()的分布的$\frac{\alpha}{2}$分位数。b为g()的分布的$1-\frac{\alpha}{2}$分位数

定义2：置信限

  • 声明
    $$
    总体分布族{P_\theta:\theta\in\Theta}\
    参数\theta,统计量T(x_1,\dotsm,x_n),置信区间1-\alpha
    $$
  • 条件
    $$
    若：P_\theta{\theta\geq T_1()}\geq 1-\alpha
    $$
  • 结论
    $$
    则：T_1为参数\theta置信水平为1-\alpha的置信下限
    $$
  • 条件
    $$
    若：P_\theta{\theta\leq T_2()}\geq 1-\alpha
    $$
  • 结论
    $$
    则：T_2为参数\theta置信水平为1-\alpha的置信上限
    $$

3 题型总结

给定置信水平求置信区间。

  • 使用定义法写出置信区间的概率公式