分治法

1 分治法概述

基本思想

  • 求解问题算法的复杂性一般都与问题规模相关，问题规模越小越容易处理。
  • 分治法的基本思想是，将一个难以直接解决的大问题，分解为规模较小的相同类型的子问题，直至这些子问题容易直接求解，并且可以利用这些子问题的解求出原问题的解。各个击破，分而治之。
  • 分治法产生的子问题一般是原问题的较小模式，这就为使用递归技术提供了方便。递归是分治法中最常用的技术。

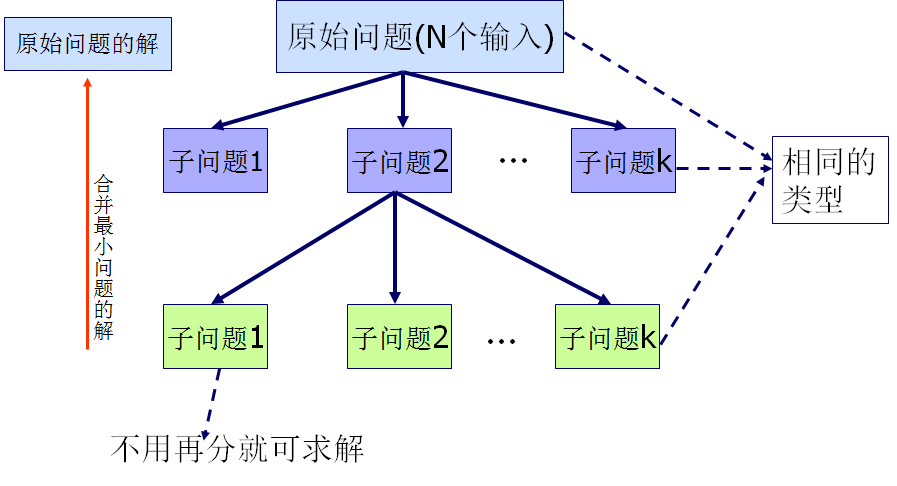
分治法解决问题的先决条件

  • 该问题的规模缩小到一定的程度就可以容易地解决；
  • 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质；
  • 利用该问题分解出的子问题的解可以合并为该问题的解；
  • 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

分治法的步骤

一般来说，分治法的求解过程由以下三个阶段组成：

  1. 划分divede：既然是分治，当然需要把规模为n的原问题划分为k个规模较小的子问题，并尽量使这k个子问题的规模大致相同。
  2. 解决conquer：各子问题的解法与原问题的解法通常是相同的，可以用递归的方法求解各个子问题，有时递归处理也可以用循环来实现。
  3. 合并merge：把各个子问题的解合并起来，合并的代价因情况不同有很大差异，分治算法的有效性很大程度上依赖于合并的实现。

在用分治法设计算法时，最好使子问题的规模大致相同。即将一个问题分成大小相等的k个子问题的处理方法是行之有效的。这种使子问题规模大致相等的做法是出自一种平衡(balancing)子问题的思想，它几乎总是比子问题规模不等的做法要好。

1
2
3
4
5
6
7
8
divide-and-conquer(P){
    if ( | P | <= n0) adhoc(P);   //解决小规模的问题
    divide P into smaller subinstances P1,P2,...,Pk；//分解问题
    for (i=1; i<=k; i++)
        yi=divide-and-conquer(Pi);  //递归的解各子问题
    return merge(y1,...,yk);  //将各子问题的解合并为原问题的解
  }

分治法的复杂性

即递归法的时间复杂性。递归求解各个子问题。递归是实现分治算法的手段。

可以通过过计算递归法的时间复杂度，计算分治法的时间复杂度。

2 减治法概述

基本思想

一个问题给定实例的解和同样问题较小实例的解之间的关系。一旦建立了这样一种关系，我们既可以递归地，也可以非递归地地来运用减治技术。

分类

  • 减去一个常量 (decrease by a constant)
  • 减去一个常数因子(decrease by a constant factor)
  • 减去的规模是可变的(variable size decrease)

算法原理

  • 在减常量变种中，每次算法迭代总是从实例规模中减去一个规模相同的常量。经常地，这个常量等于一。函数f(n) = an可以用一递归定义来计算
1
2
f(n) =　f (n-1) *a		如果n > 1
	 =	a			如果n = 1

  • 减常因子技术意味着在算法的每次迭代中，总是从实例的规模中减去一个相同的常数因子。在多数应用中，这样的常数因子等于二。例如：计算an的值是规模为n的实例：an = (an/2)2。O(log n);

  • 在减治法的减可变规模变种中，算法在每次迭代时，规模减小的模式都是不同的。例如：欧几里得算法：gcd (m,n) = gcd (n, m mod n)

算法效率

与蛮力法相同。但是思想不同。

与分治法对比

该算法和基于分治思想的算法有所不同:

  • 分治法分解成规模相似的类型相同的子问题。
  • 减治法直接通过运算将问题的规模减小。问题数量没有增加。

3 变治法概述

基本思想

  1. 变换为同样问题的一个更简单或者更方便 的实例—实例化简(Instance simplification)。
  2. 变换为同样实例的不同表现—改变表现(Representation Change).
  3. 变换为另一个问题的实例， 这种问题的算法是已知的—问题化简(Problem reduction).

根本上是转换问题的思路。

4 分治法应用

1排列问题√

9整数划分问题√

二分搜索问题√

2大数乘法√

3矩阵乘法√

快速排序√

合并排序√

线性时间选择√

8最近点对问题√

10棋盘覆盖问题√

7数组中的逆序对√

5 减治法应用

4拓扑排序√

11生成子集√

假币问题

俄式乘法

5约瑟夫问题√

gcd欧几里得算法

插值查找√

二叉树查找√

6 变治法应用

6元素唯一性-预排序算法√

模式计算-预排序算法

线性方程组-高斯消去算法

霍纳法则

lcm最小公倍数

AVL树√

2-3树√

堆排序√

二进制幂√