Huffman算法

Huffman算法

问题描述

  • 一个字符串文件，我们希望尽可能多地压缩文件，但源文件能够很容易地被重建。

  • 用特定的比特串表示每个字符，称为字符的编码，文件的大小取决于文件中的字符数n。我们可以使用一种定长编码，对每个字符赋予一个长度同为m (m≥log2n)的比特串。

  • 设文件中的字符集是C={c1,c2,…, cn}, 又设f(ci), 1≤i≤n,是文件中字符ci的频度，即文件中ci出现的次数。

  • 由于有些字符的频度可能远大于另外一些字符的频度，所以用变长的编码。

  • 去除编码的二义性：

  • 当编码在长度上变化时，我们规定一个字符的编码不能是另一个字符编码的前缀（即词头），这种码称为前缀码。

  • 例如，如果我们把编码10和101赋予字符“a” 和“b”就会存在二义性，不清楚10究竟是“a” 的编码还是字符“b”的编码的前缀。

  • 一旦满足前缀约束，编码即不具备二义性，可以扫描比特序列直到找到某个字符的编码。

算法原理

  • 由Huffman算法构造的编码满足前缀约束，并且最小化压缩文件的大小。算法重复下面的过程直到C仅由一个字符组成：
    • 设ci和cj是两个有最小频度的字符，建立一个新节点c，它的频度是ci和cj频度的和，使ci和cj为c的子节点，
    • 令C = （C-{ci, cj}）∪{c}。

算法过程

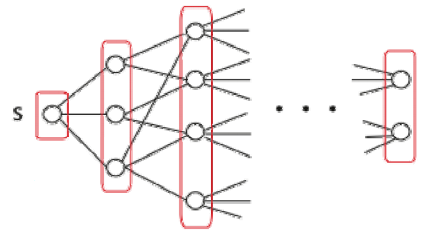
  1. 第一步：初始化n个单节点的树，为它们标上字母表的字符。把每个字符的概率记在树的根中，用来指出树的权重（更一般地来说，树的权重等于树中所有叶子的概率之和）。

  2. 第二步：重复下面的步骤，直到只剩一棵单独的树：

    • 找到两棵权重最小的树， 把它们作为新树中的左右子树，并把其权重之和作为新的权重记录在新的根中。

  3. 构建树后然后进行编码，从根节点，每个路径上左0右1

算法效率

$O(n/log n)$

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
算法HUFFMAN
输入：n个字符的集合C={c1,c2,…, cn}和它们的频度{f(c1), f(c2),…, f(cn)}。
输出：C的Huffman树（V，T）。

根据频度将所有字符插入最小堆H
V←C； T={}
for j←1 to n-1
 	c←DELETEMIN(H)
 	c’←DELETEMIN(H)
 	f(v) ← f(c)+ f(c’)	//新节点v
 	INSERT (H, v)
 	V =V∪{v}	
 	T = T∪{(v, c), (v, c’)}  // c, c’为T中v的孩子
end for