01背包问题

1 01背包问题-回溯法

问题描述

将物品放到背包中。

  • n件物品
  • 每件物品的重量为w[i]
  • 价值为v[i]
  • m个背包
  • 每个背包的容量为c[j]

求背包装载的最大价值。或者是否能装下所有。

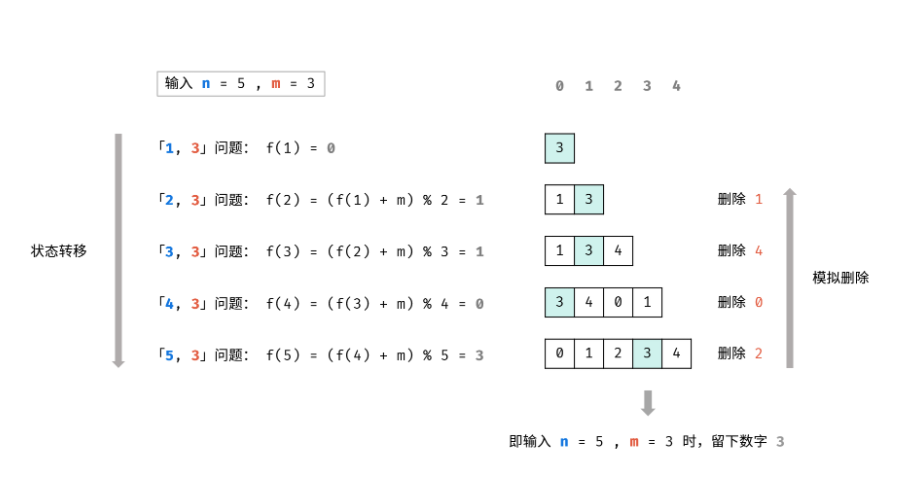
具体问题n=3，C=20，(v1,v2,v3)=(20,15,25)， (w1,w2,w3)=(10,5,15)，求X=(x1,x2,x3)使背包价值最大？

问题分析

  • 解空间是子集树
  • 可行性约束函数（剪枝函数）$\sum w_ix_i\leq c_i$

算法原理

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
template<class Typew, class Typep>
Typep Knap<Typew, Typep>::Bound(int i)
{// 计算上界
   Typew cleft = c - cw;  // 剩余容量
   Typep b = cp;
   // 以物品单位重量价值递减序装入物品
   while (i <= n && w[i] <= cleft) {
      cleft -= w[i];
      b += p[i];
      i++;
      }
   // 装满背包
   if (i <= n) b += p[i]/w[i] * cleft;
   return b;
}

2 01背包问题-分支限界

问题描述

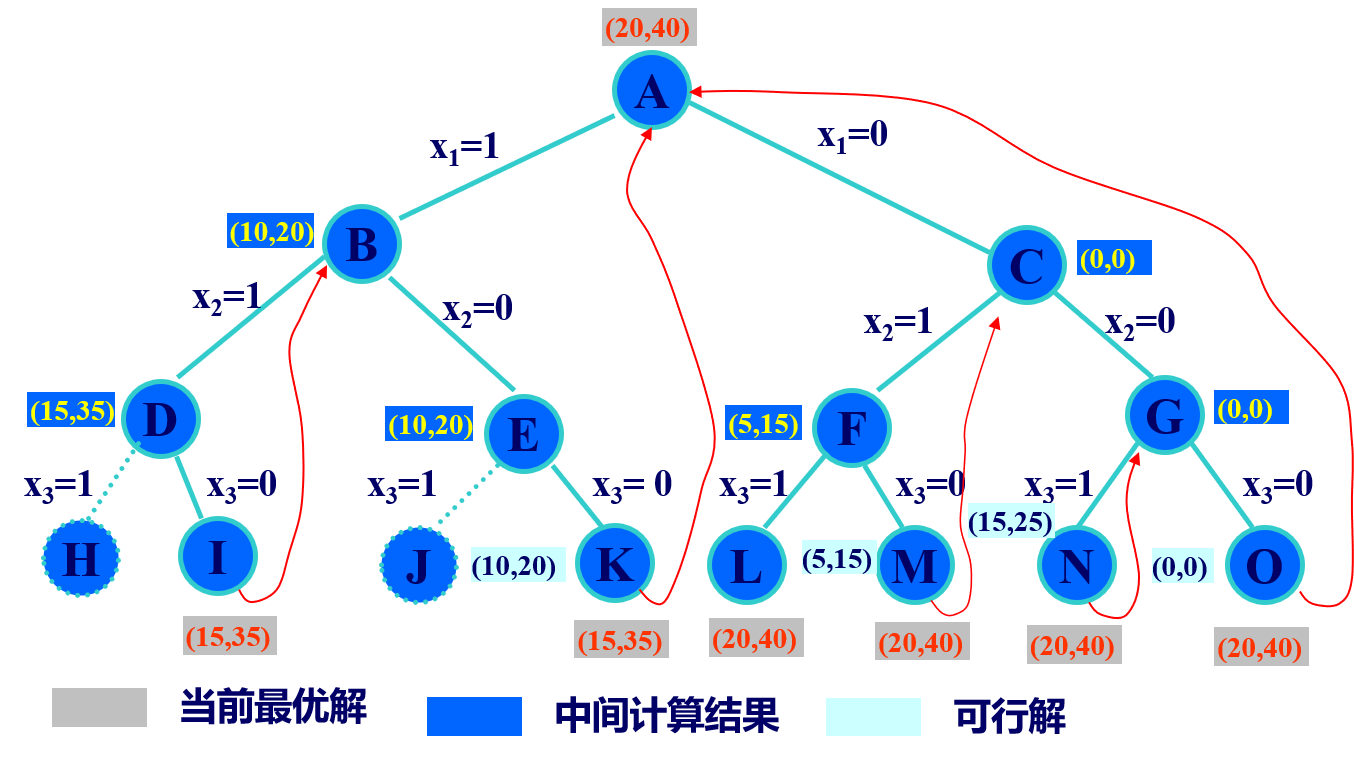
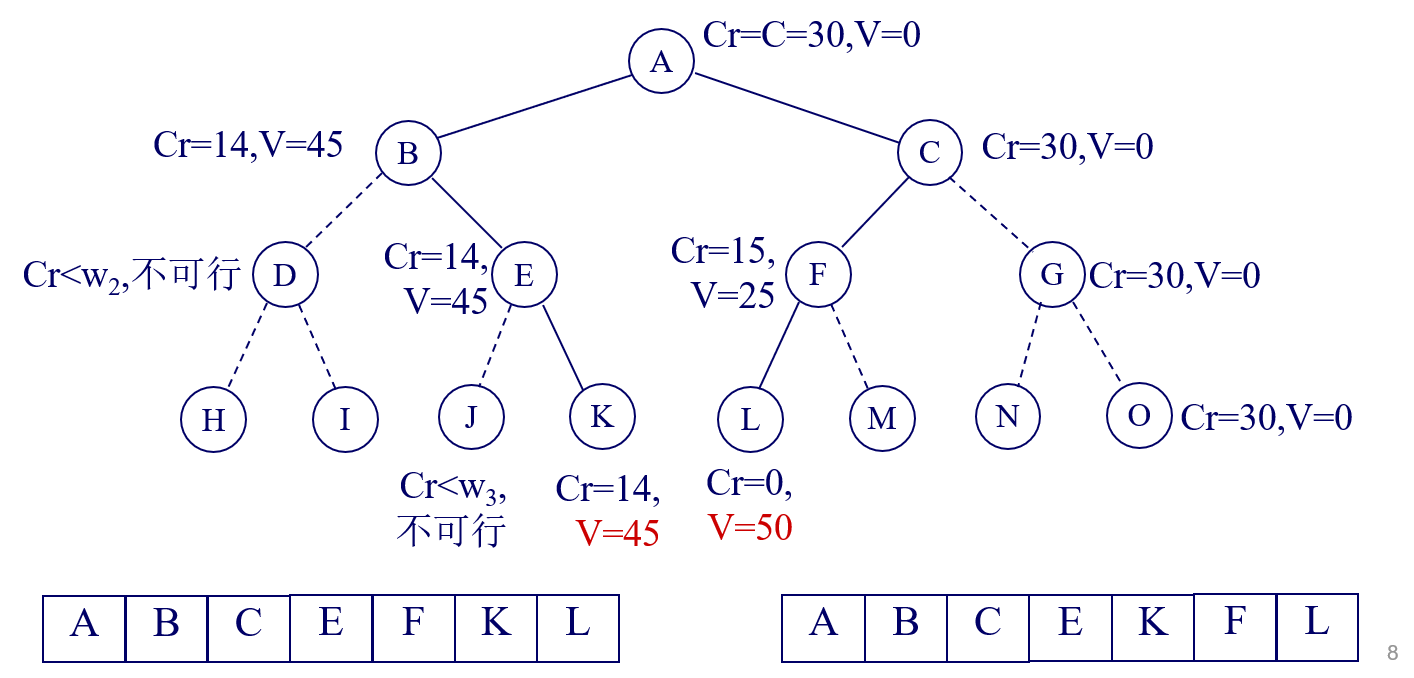
0-1背包问题： （分析队列式与优先队列式过程）
n=3, C=30, w={16, 15, 15}, v={45, 25, 25}

问题分析

算法原理

算法实现

3 01背包问题-动态规划

问题描述

0/1（同类物品数最大1）背包问题可以定义如下：
设U={u1,u2,…,un}是一个准备放入容量为C的背包中的n项物品的集合。对于1≤j≤n,令sj和vj分别为第j项物品的体积和价值，C,sj,vj和j 都是正整数。
要解决的问题是用U中的一些物品来装 背包，这些物品的总体积不超过C，然而要使它们的总价值最大。

问题分析

导出递归公式，
设V[i,j] 表示从前i项{u1，u2，…,ui}中取出来的装入体积为j的背包的物品的最大价值。这里，i的范围是从0到n, j的范围是从0到C。
则，要寻求的是值V[n,C]。
有V[0,j]对于所有j的值是0，当背包中没有物品。
V[i,0]对于所有i的值为0，当没有物品可放到容积为0的背包里。

算法原理

1
2
3
V[i,j]	 = 0					若i=0或j=0
			=V[i-1,j]				若j<si
			=Max{V[i-1,j],V[i-1,j-si]+vi} 		若j≥si