量的定义

定义n维数组，并且在数组上进行简单的变换与操作。

名称

  • 标量，单个数据，零阶张量，
  • 向量，一维数组，一阶张量，
  • 矩阵，二维数组，二阶张量
  • 张量，高维数组，张量，

关系

  • 可以使用向量，来定义n维线性空间、n维向量空间。向量，以数学的方式描述n维线性空间。标量、向量、矩阵、张量是对n维线性空间的暴力展开。
  • 维数：数组总共有多少个维度。3维
  • 维度：数组每个维的长度是多少。维度是(2,3,4)
  • 范数：用来衡量数组的特征。F1范数，绝对值之和。F2范数，平方和。
  • 列表和张量不同。列表的低维的维度可以不同。[[1],[1,2]]。张量，相同维的维度必须一致。
  • 对于张量的描述可以使三阶，一阶二维，二阶三维，三阶四维。
  • 对于数组的描述，应该是三维数组，一维维度是2，二维维度是3，三维维度是4
  • 向量描述n维线性空间，向量的维度描述线性空间维度的个数，向量的数据描述每个维度的大小。
  • 高维是外层的，低维是内层的。高维包含多个低维。低维能锁定更精确的数据。高维可以索引低维。

运算

  • 同维度的四则运算，对应位运算。

  • 不同维度的四则运算，进行广播。

  • 点乘，同维度，同位置相乘相加。
    点乘，不同维度，

维度说明

ndarray(多维数组)是Numpy处理的数据类型。多维数组的维度即为对应数据所在的空间维度，1维可以理解为直线空间，2维可以理解为平面空间，3维可以理解为立方体空间。

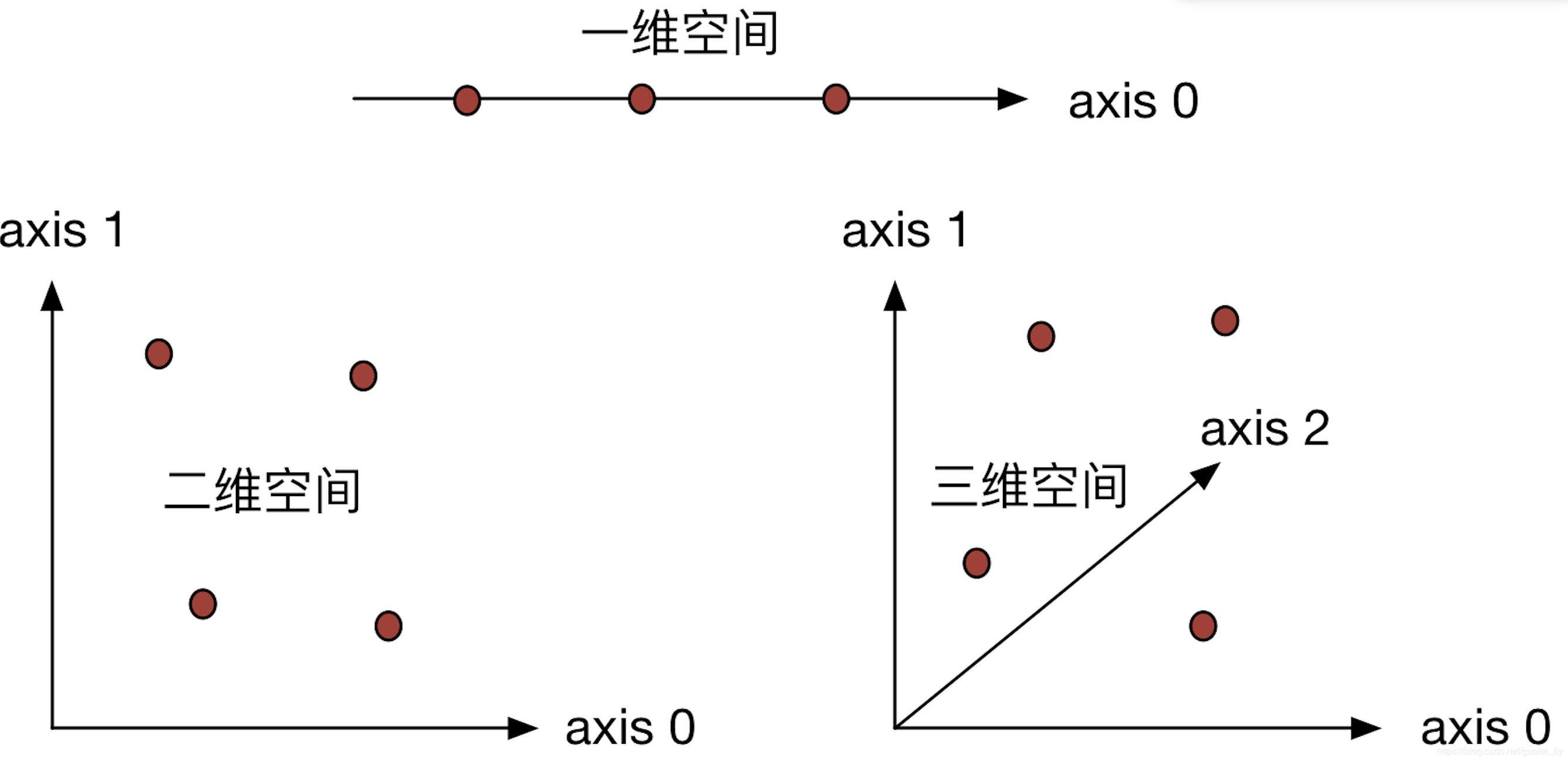
  • 轴是用来对多维数组所在空间进行定义、描述的一组正交化的直线，根据数学惯例可以用i,j,ki, j ,ki,j,k来表示。

  • 在一维空间中，用一个轴就可以表示清楚，numpy中规定为axis 0，空间内的数可以理解为直线空间上的离散点 (x i, )。

  • 在二维空间中，需要用两个轴表示，numpy中规定为axis 0和axis 1，空间内的数可以理解为平面空间上的离散点（x i，y j）。

  • 在三维空间中，需要用三个轴才能表示清楚，在二维空间的基础上numpy中又增加了axis 2，空间内的数可以理解为立方体空间上的离散点（x i，y j，z k）。

Python中可以用numpy中的ndim和shape来分别查看维度，以及在对应维度上的长度。直观上可以根据符号“[ ]”的层数来判断，有m层即为m维，最外面1层对应axis0， 依次为axis1，axis2…