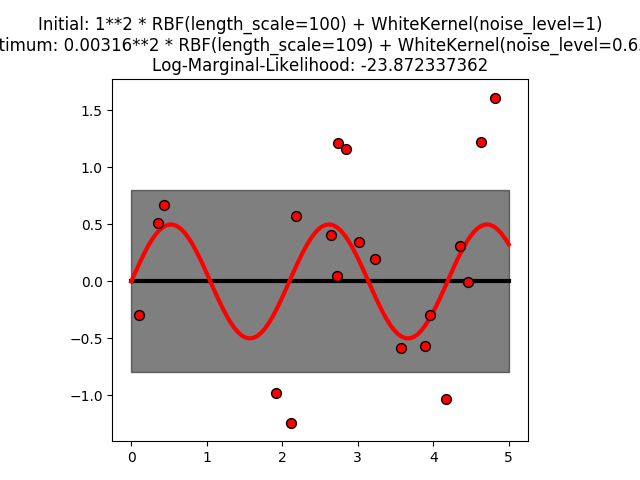
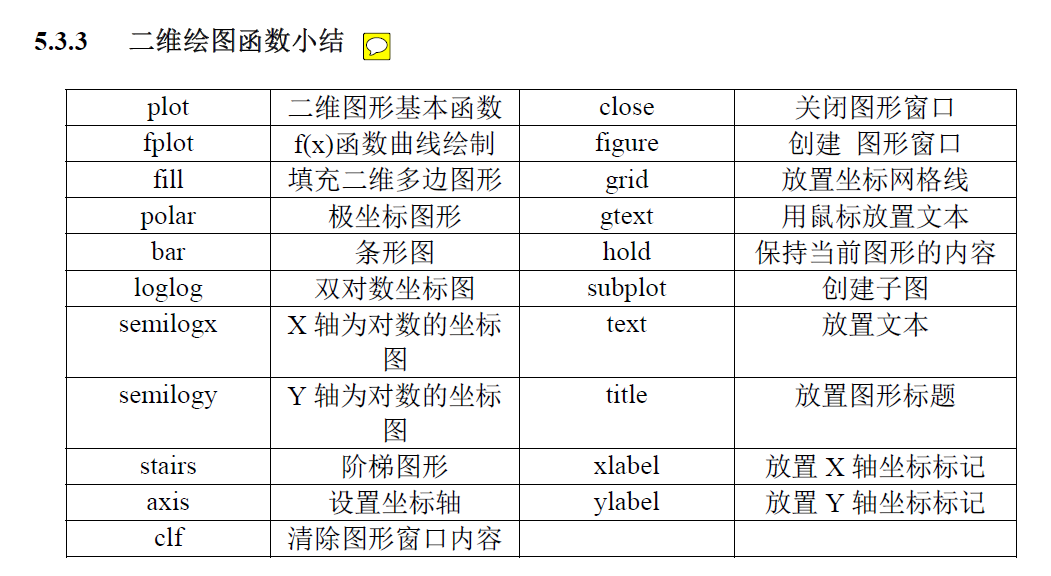
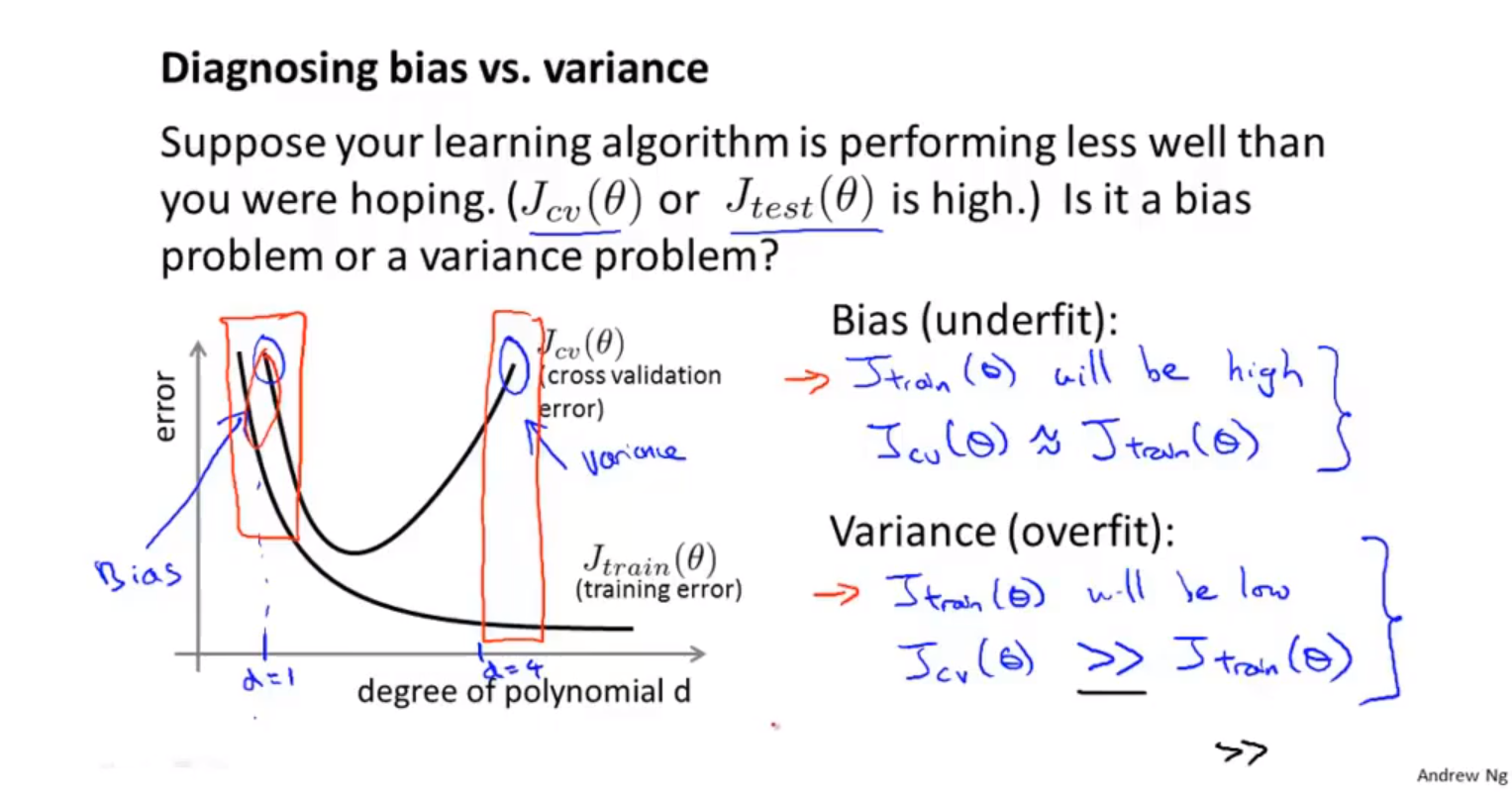
3D与动画

基本方法

本章知识点归纳如下:

创建3D图：ax = Axes3D(fig)
画出3D图：ax.plot_surface()
投影：ax.contourf()
动画：animation.FuncAnimation()

3D作图

首先在进行 3D Plot 时除了导入 matplotlib ，还要额外添加一个模块，即 Axes 3D 3D 坐标轴显示,并且之后要先定义一个图像窗口，在窗口上添加3D坐标轴，显示成下图：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = Axes3D(fig)

接下来给进 X 和 Y 值，并将 X 和 Y 编织成栅格。每一个（X, Y）点对应的高度值我们用下面这个函数来计算:

# X, Y value
X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(X, Y)    # x-y 平面的网格
R = np.sqrt(X ** 2 + Y ** 2)
# height value
Z = np.sin(R)

做出一个三维曲面，并将一个 colormap rainbow 填充颜色，之后将三维图像投影到 XY 平面上做一个等高线图。其中，rstride 和 cstride 分别代表 row 和 column 的跨度。跨度越小，图形上的网格越密集，实际画出的 plot 3D 图像会如下图所示：

fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow'))
<mpl_toolkits.mplot3d.art3d.Poly3DCollection at 0x7fcec6cf8320>

投影

有时候我们在观察3D图形时，可能需要图形映射到平面中来观察。还记得之前学习过的等高线图吗，它可以帮助我们对3D图像进行投影。下面代码为添加 XY 平面的等高线,如果 zdir 选择了x，那么效果将会是对于 XZ 平面的投影，而调整offset可以调整投影出现的位置，整体效果如下：

fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow'))
ax.contourf(X, Y, Z, zdir='z', offset=-1, cmap=plt.get_cmap('rainbow'))
<matplotlib.contour.QuadContourSet at 0x7fcec4b6aba8>

如果 zdir 选择了x，那么效果将会是对于 XZ 平面的投影，效果如下：

fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow'))
ax.contourf(X, Y, Z, zdir='x', offset=-4, cmap=plt.get_cmap('rainbow'))
<matplotlib.contour.QuadContourSet at 0x7fcec4919a90>

Animation 动画

最后，matplotlib还为我们提供了动画的接口。我们将使用其中一种方式 function animation 来为大家讲解，具体可参考matplotlib animation api。下面，我们就开始吧！

导入动画库并定义方程
我们的数据是一个0~2π内的正弦曲线：

from matplotlib import pyplot as plt
from matplotlib import animation
import numpy as np

fig, ax = plt.subplots()

x = np.arange(0, 2*np.pi, 0.01)
line, = ax.plot(x, np.sin(x))

构造动画函数与帧函数：
接着，构造自定义动画函数animate，用来更新每一帧上各个x对应的y坐标值，参数表示第i帧；然后，构造开始帧函数init：

def animate(i):
    line.set_ydata(np.sin(x + i/10.0))
    return line,
def init():
    line.set_ydata(np.sin(x))
    return line,

参数设置：
接下来，我们调用FuncAnimation函数生成动画。参数说明：
1. fig 进行动画绘制的figure
2. func 自定义动画函数，即传入刚定义的函数animate
3. frames 动画长度，一次循环包含的帧数
4. init_func 自定义开始帧，即传入刚定义的函数init
5. interval 更新频率，以ms计
6. lit 选择更新所有点，还是仅更新产生变化的点。应选择True，但mac用户请选择False，否则无法显示动画

(因为平台的不兼容问题，请klab暂时无法进行动画的演示，请大家在自己的电脑上尝试进行动画作图吧~)

fig, ax = plt.subplots()
line, = ax.plot(x, np.sin(x))

ani = animation.FuncAnimation(fig=fig,
                              func=animate,
                              frames=100,
                              init_func=init,
                              interval=20,
                              blit=True)
plt.show()

当然，你也可以将动画以mp4格式保存下来，但首先要保证你已经安装了ffmpeg 或者mencoder

1	ani.save('basic_animation.mp4', fps=30, extra_args=['-vcodec', 'libx264'])

练一练

请大家根据之前所学的3D图画法画出3D数据 z = (x + y)^2，并利用等高线图对其进行投影。

#参考答案：
X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(X, Y)    
Z = (X + Y)**2

fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow'))
ax.contourf(X, Y, Z, zdir='x', offset=-4, cmap=plt.get_cmap('rainbow'))
<matplotlib.contour.QuadContourSet at 0x7fcec4416400>