过拟合

偏差

  • bias
  • 是系统性误差，由于模型本身引起的。

方差

  • var
  • 是样本数据误差，由于样本数据的随机性引起的。

欠拟合与过拟合

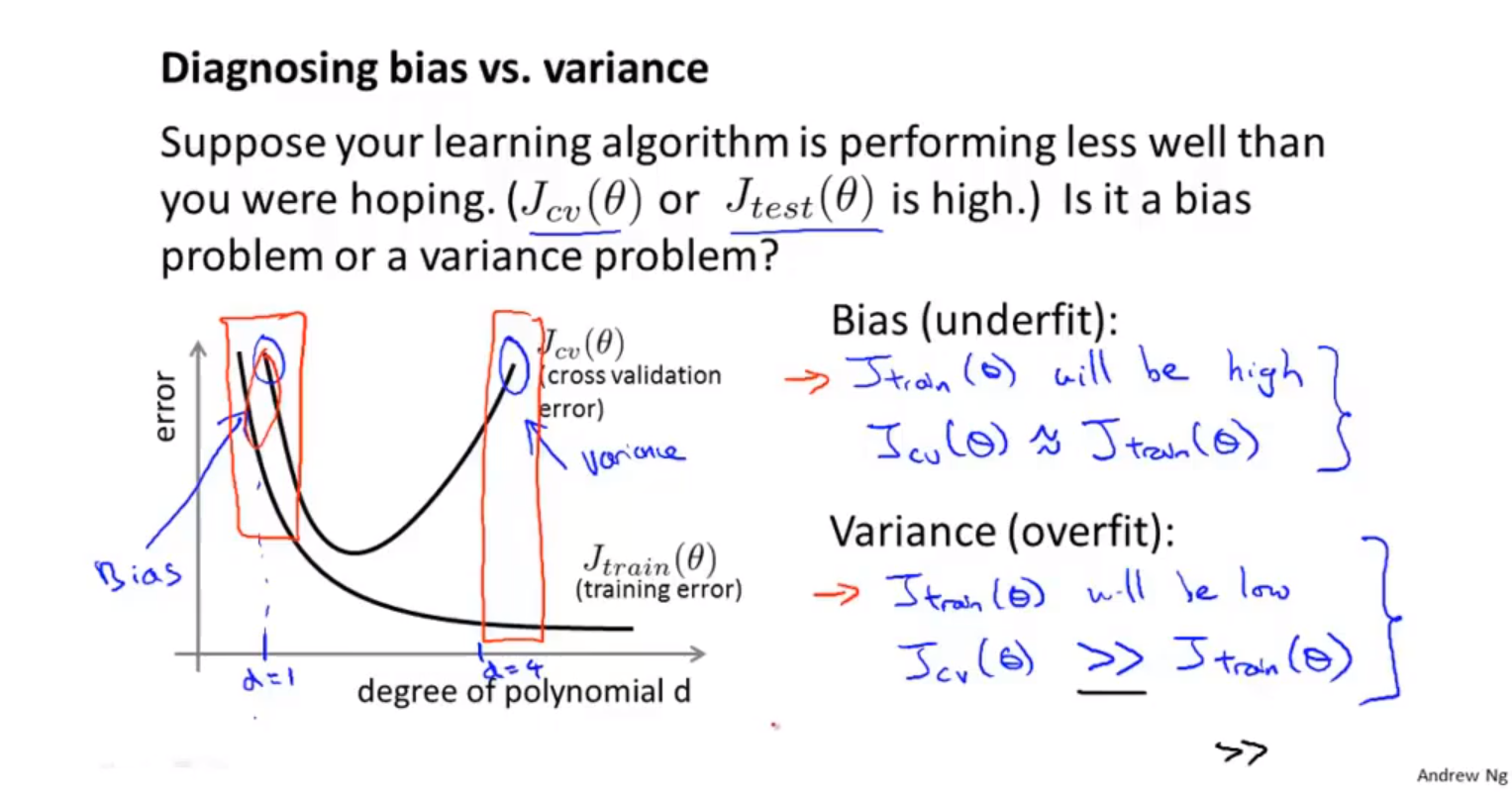
jtrain训练集的代价函数。jcv交叉验证集的代价函数。jtrain能够通过训练过程，将样本随机性引起的误差降到最低。jcv没有经过训练过程，会最大化样本的随机性方差和模型本身的偏差。

  • 高偏差：Jtrain和Jcv都很大，并且Jtrain≈Jcv。对应欠拟合。欠拟合的时候，由模型本身和样本的随机性引起的误差都很大。
  • 高方差：Jtrain较小，Jcv远大于Jtrain。对应过拟合。过拟合后由样本随机性引起的误差会非常大。
  • 低方差，高偏差。变量过多的时候出现的，训练得到的假设函数能够很好的拟合训练集，代价函数非常小。但是无法泛化到新的样本当中。

解决办法

  • 减少特征的数量
  • 对特征进行正则化。

正则化

  • 代价函数加入正则化的数据项，用来缩小每一个参数。

  • 现行回归的正则化代价函数
    $$
    J(\theta) = \frac{1}{2m}[\sum_1^m(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_1^n\theta^2_j]
    $$

  • 逻辑回归的正则化，二者一致。

$$
J(\theta)=-\frac{1}{m}[\sum_i^my^{(i)}\log h_\theta(x^{(i)})+(1-y^{(i)})\log (1-h_\theta (x^{(i)}))]+\frac{\lambda}{2m}\sum_1^n\theta_j^2
$$

编程任务

线性回归

  • 添加，高阶的编程项.
  • 对参数进行正则化，并对比正则化前后假设函数的不同。
  • 需要绘制，拟合过程参数变化率（梯度下降速度。
  • 需要绘制，拟合完成后假设函数（假设函数的最终形状。判断是否过拟合。

逻辑回归

  • 添加，高阶的编程项.
  • 对参数进行正则化，并对比正则化前后假设函数的不同。
  • 需要绘制，拟合过程参数变化率（梯度下降速度。
  • 需要绘制，拟合完成后假设函数（假设函数的最终形状。判断是否过拟合。