支持向量机

支持向量机的定义

  • 逻辑回归的假设函数（sigmod）函数，将离散的分类，变成了连续的输出。建立与连续特征的函数关系。
  • 支持向量机的假设函数，将sigmod非线性函数改为分段的线性函数。用来简化运算。

假设函数

  • 支持向量机本身并没有给出假设函数。其本质上并不需要拟合出假设函数？不不不，支持向量机的假设函数
    $$
    h(\theta)=\theta^T * x
    $$

代价函数

  • 支持向量机的代价函数

$$
J(\theta) =C \sum_1^m(y^{(i)}cost_1(\theta^Tx)+(1-y^{(i)})cost_0(\theta^Tx))+\frac{1}{2}\sum_1^n\theta_j^2
\
min (J(\theta))
$$

支持向量机的原理

  • 大间距分类器。支持向量机会使得两个类别之间保持更大的安全距离。

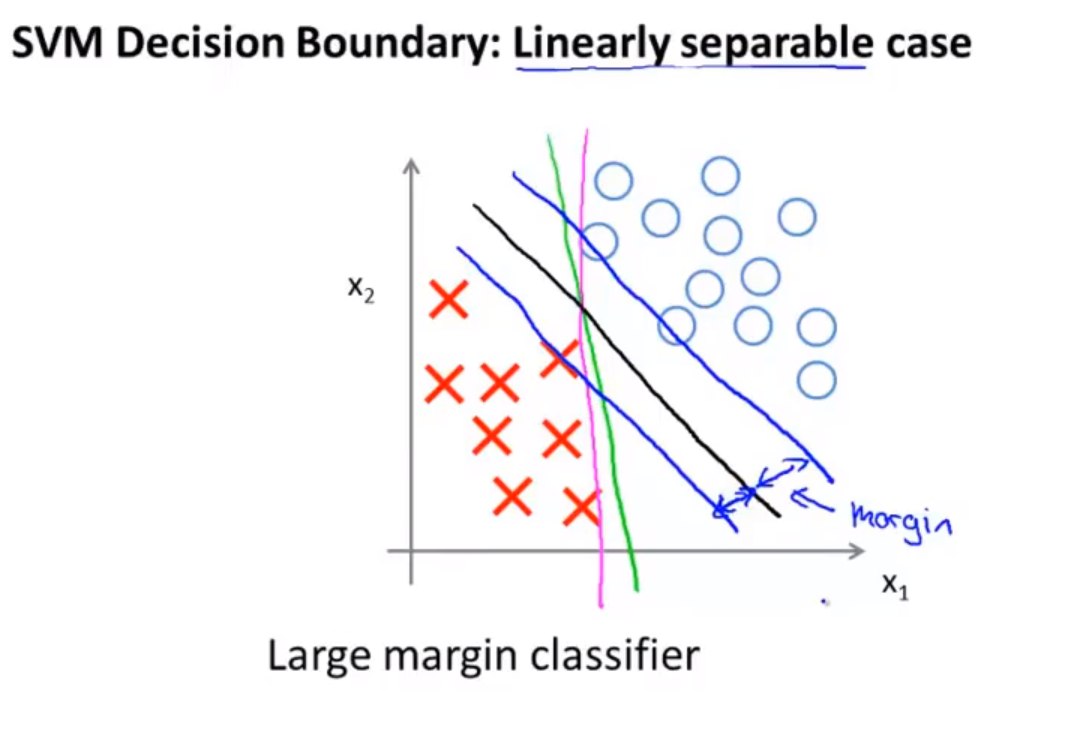
  • 参数C能够决定假设函数对数据的敏感程度。

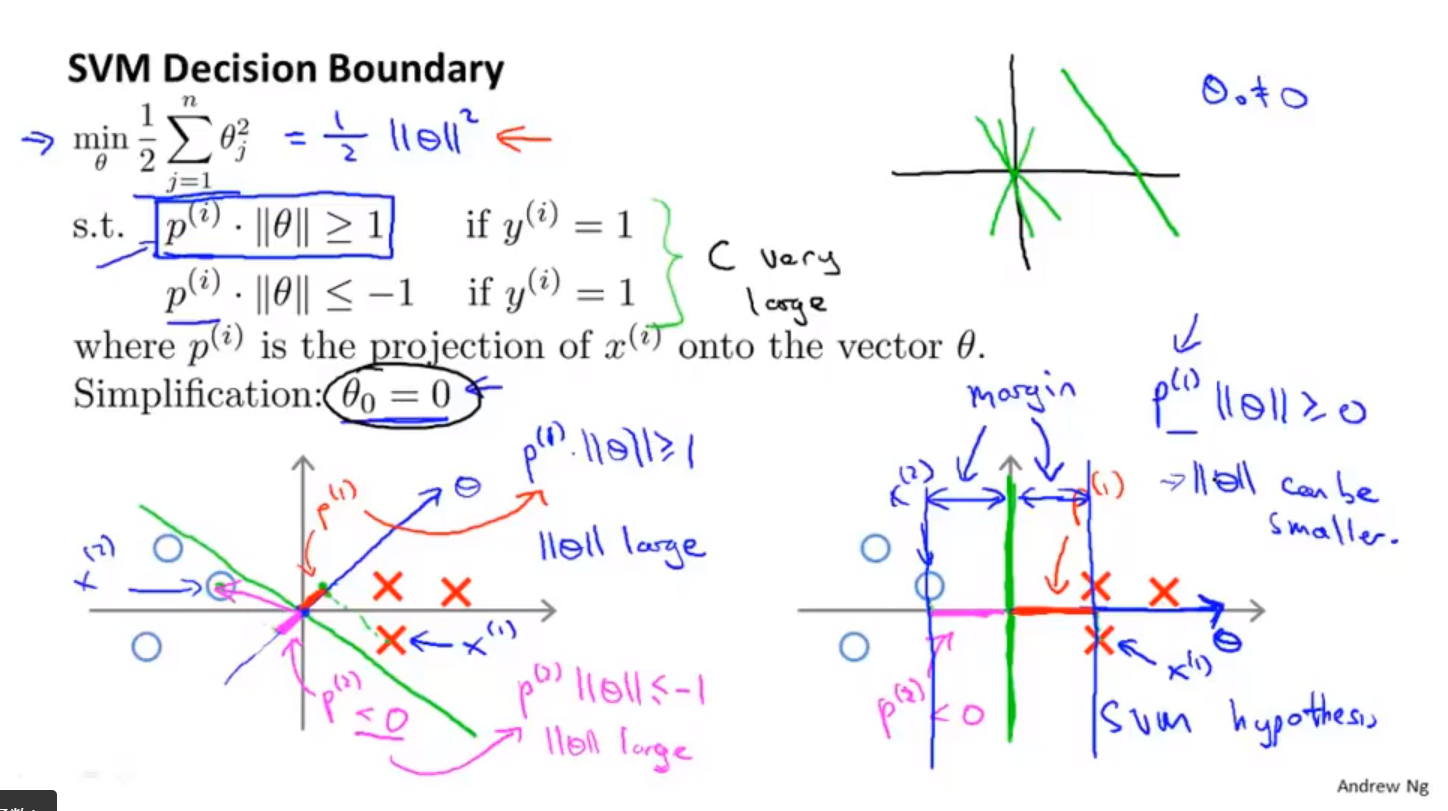
大间距分类器的数学原理

  • $\theta^T*x$可以看做两个向量的內积
  • 这个值越大，说明x在$\theta$方向的投影p越大，这个值越小，说明x在$\theta$方向的投影越小（为赋值）。为了能找到最大投影差，一般会选择类别差距最大的$\theta$值，此时，决策边界，为$\theta$向量的垂直线。

核函数与支持向量机算法

主要介绍了核函数。高斯函数

  • 目标：训练复杂的非线性判别边界。
  • 主要包括两部分：参数向量和特征向量。
  • 特征向量使用核函数来描述。

假设函数

$$
h(\theta)=\theta_0+\theta_1f_1+\theta_2f_2+\theta_3*f_3+\dots
$$

  • f用来代理数据集的某个特征，这个特征可能是多项式一个项，也可能是更复杂的函数。
  • f描述的特征可能是没有必要的，此时$\theta$可能是0

高斯核函数描述特征向量

  • 选取三个点，作为特征的核。

  • 然后以样本点为中心的高斯核函数作为新的特征。

  • 定义相似度函数=高斯核函数（也可以等于其他的函数）
    $$
    f_i = similarity(x,l^{(i)}) \= \exp(-\frac{||x-l||^2}{2\sigma^2})
    $$

  • 选取样本点作为相似度函数的中心。

使用核函数的支持向量机算法

支持向量机算法应该也可以不使用核函数。

  • 给定样本
  • 选取样本中的部分点，作为核函数的核心
  • 最小化代价函数

$$
J(\theta) =C \sum_1^m(y^{(i)}cost_1(\theta^Tf)+(1-y^{(i)})cost_0(\theta^Tf))+\frac{1}{2}\sum_1^n\theta_j^2
\
min (J(\theta))
$$

支持向量机的参数选择

使用SVM

使用SVM软件包解决SVM向量机的参数求解问题

  • 选择合适的参数C
  • 选择相似函数（内核函数）
    • 线性核函数（没有核函数）$\theta^T*x$
    • 高斯核函数（选择$\sigma$的值）$f_i= \exp(-\frac{||x-l||^2}{2\sigma^2})$(l是选择的特征点)
    • 多项式核函数$(x^T*l+constan)^degree$
    • string kernel，chi-square kernel，intersection kernel

逻辑回归与SVM选择

  • 当n>m时，特征个数>训练样本数，使用逻辑回归或者线性内核的SVM