04特殊应用:人脸识别和神经风格迁移
特殊应用:人脸识别和神经风格转换
1 人脸识别
定义
人脸验证(Face Verification) 和 人脸识别(Face Recognition) 的区别:
- 人脸验证:一般指一个一对一问题,只需要验证输入的人脸图像是否与某个已知的身份信息对应;
- 人脸识别:一个更为复杂的一对多问题,需要验证输入的人脸图像是否与多个已知身份信息中的某一个匹配。
一般来说,由于需要匹配的身份信息更多导致错误率增加,人脸识别比人脸验证更难一些。
2 One-Shot 学习
人脸识别所面临的一个挑战是要求系统只采集某人的一个面部样本,就能快速准确地识别出这个人,即只用一个训练样本来获得准确的预测结果。这被称为One-Shot 学习。
有一种方法是假设数据库中存有 N 个人的身份信息,对于每张输入图像,用 Softmax 输出 N+1 种标签,分别对应每个人以及都不是。然而这种方法的实际效果很差,因为过小的训练集不足以训练出一个稳健的神经网络;并且如果有新的身份信息入库,需要重新训练神经网络,不够灵活。
因此,我们通过学习一个 Similarity 函数来实现 One-Shot 学习过程。Similarity 函数定义了输入的两幅图像的差异度,其公式如下:
$$Similarity = d(img1, img2)$$
- 可以设置一个超参数 $τ$ 作为阈值,作为判断两幅图片是否为同一个人的依据。
3 Siamese 网络
- 实现 Similarity 函数的一种方式是使用Siamese 网络,它是一种对两个不同输入运行相同的卷积网络,然后对它们的结果进行比较的神经网络。
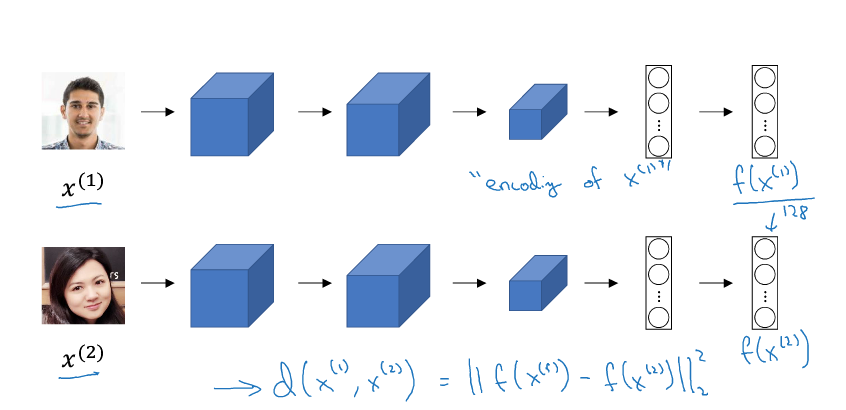
- 如上图示例,将图片 $x^{(1)}$、$x^{(2)}$ 分别输入两个相同的卷积网络中,经过全连接层后不再进行 Softmax,而是得到特征向量 $f(x^{(1)})$、$f(x^{(2)})$。这时,Similarity 函数就被定义为两个特征向量之差的 L2 范数:
$$d(x^{(1)}, x^{(2)}) = ||f(x^{(1)}) - f(x^{(2)})||^2_2$$
相关论文:Taigman et al., 2014, DeepFace closing the gap to human level performance
4 人脸识别与Triplet 损失
- Triplet 损失函数 用于训练出合适的参数,以获得高质量的人脸图像编码。“Triplet”一词来源于训练这个神经网络需要大量包含 Anchor(靶目标)、Positive(正例)、Negative(反例)的图片组,其中 Anchor 和 Positive 需要是同一个人的人脸图像。

- 对于这三张图片,应该有:
$$||f(A) - f(P)||^2_2 + \alpha \le ||f(A) - f(N)||^2_2$$
其中,$\alpha$ 被称为间隔(margin),用于确保 $f()$ 不会总是输出零向量(或者一个恒定的值)。
Triplet 损失函数的定义:
$$L(A, P, N) = max(||f(A) - f(P)||^2_2 - ||f(A) - f(N)||^2_2 + \alpha, 0)$$
其中,因为 $||f(A) - f(P)||^2_2 - ||f(A) - f(N)||^2_2 + \alpha$ 的值需要小于等于 0,因此取它和 0 的更大值。
对于大小为 $m$ 的训练集,代价函数为:
$$J = \sum^m_{i=1}L(A^{(i)}, P^{(i)}, N^{(i)})$$
通过梯度下降最小化代价函数。
在选择训练样本时,随机选择容易使 Anchor 和 Positive 极为接近,而 Anchor 和 Negative 相差较大,以致训练出来的模型容易抓不到关键的区别。因此,最好的做法是人为增加 Anchor 和 Positive 的区别,缩小 Anchor 和 Negative 的区别,促使模型去学习不同人脸之间的关键差异。
相关论文:Schroff et al., 2015, FaceNet: A unified embedding for face recognition and clustering
5 人脸验证与二分类结构
- 除了 Triplet 损失函数,二分类结构也可用于学习参数以解决人脸识别问题。其做法是输入一对图片,将两个 Siamese 网络产生的特征向量输入至同一个 Sigmoid 单元,输出 1 则表示是识别为同一人,输出 0 则表示识别为不同的人。
- Sigmoid 单元对应的表达式为:
$$\hat y = \sigma (\sum^K_{k=1}w_k|f(x^{(i)})_{k} - x^{(j)})_{k}| + b)$$
- 其中,$w_k$ 和 $b$ 都是通过梯度下降算法迭代训练得到的参数。上述计算表达式也可以用另一种表达式代替:
$$\hat y = \sigma (\sum^K_{k=1}w_k
\frac{(f(x^{(i)})_k - f(x^{(j)})_k)^2}{f(x^{(i)})_k + f(x^{(j)})_k} + b)$$
- 其中,$\frac{(f(x^{(i)})_k - f(x^{(j)})_k)^2}{f(x^{(i)})_k + f(x^{(j)})_k}$ 被称为 $\chi$ 方相似度。
- 无论是对于使用 Triplet 损失函数的网络,还是二分类结构,为了减少计算量,可以提前计算好编码输出 $f(x)$ 并保存。这样就不必存储原始图片,并且每次进行人脸识别时只需要计算测试图片的编码输出。
6 什么是神经风格迁移
- 神经风格迁移(Neural style transfer) 将参考风格图像的风格“迁移”到另外一张内容图像中,生成具有其特色的图像。

7 深度卷积网络在学什么?
- 想要理解如何实现神经风格转换,首先要理解在输入图像数据后,一个深度卷积网络从中都学到了些什么。我们借助可视化来做到这一点。

我们通过遍历所有的训练样本,找出使该层激活函数输出最大的 9 块图像区域。可以看出,浅层的隐藏层通常检测出的是原始图像的边缘、颜色、阴影等简单信息。随着层数的增加,隐藏单元能捕捉的区域更大,学习到的特征也由从边缘到纹理再到具体物体,变得更加复杂。
简单来说,神经网络的的层数越多,学习的图片块越广泛。学习到的特征范围越大。图片快指某个隐藏层涉及到的图片的像素范围;激活值是指对当前神经元产生的激活值较大的图片块,表示该神经元学习到的图片特征。
相关论文:Zeiler and Fergus., 2013, Visualizing and understanding convolutional networks
8 代价函数
- 神经风格迁移生成图片 G 的代价函数如下:
$$J(G) = \alpha \cdot J_{content}(C, G) + \beta \cdot J_{style}(S, G)$$
其中,$\alpha$、$\beta$ 是用于控制相似度比重的超参数。
神经风格迁移的算法步骤如下:
- 随机生成图片 G 的所有像素点;
- 使用梯度下降算法使代价函数最小化,以不断修正 G 的所有像素点。
9 内容代价函数
- 上述代价函数包含一个内容代价部分和风格代价部分。我们先来讨论内容代价函数 $J_{content}(C, G)$,它表示内容图片 C 和生成图片 G 之间的相似度。
$J_{content}(C, G)$ 的计算过程如下:
- 使用一个预训练好的 CNN(例如 VGG);
- 选择一个隐藏层 $l$ 来计算内容代价。$l$ 太小则内容图片和生成图片像素级别相似,$l$ 太大则可能只有具体物体级别的相似。因此,$l$ 一般选一个中间层;
- 设 $a^{(C)[l]}$、$a^{(G)[l]}$ 为 C 和 G 在 $l$ 层的激活,则有:
$$J_{content}(C, G) = \frac{1}{2}||(a^{(C)[l]} - a^{(G)[l]})||^2$$
- $a^{(C)[l]}$ 和 $a^{(G)[l]}$ 越相似,则 $J_{content}(C, G)$ 越小。
10 风格代价函数

每个通道提取图片的特征不同,比如标为红色的通道提取的是图片的垂直纹理特征,标为黄色的通道提取的是图片的橙色背景特征。那么计算这两个通道的相关性,相关性的大小,即表示原始图片既包含了垂直纹理也包含了该橙色背景的可能性大小。通过 CNN,“风格”被定义为同一个隐藏层不同通道之间激活值的相关系数,因其反映了原始图片特征间的相互关系。
对于风格图像 S,选定网络中的第 $l$ 层,则相关系数以一个 gram 矩阵的形式表示:
$$G^{[l](S)}_{kk’} = \sum^{n^{[l]}_H}_{i=1} \sum^{n^{[l]}_W}_{j=1} a^{[l](S)}_{ijk} a^{[l](S)}_{ijk’}$$
其中,$i$ 和 $j$ 为第 $l$ 层的高度和宽度;$k$ 和 $k’$ 为选定的通道,其范围为 $1$ 到 $n_C^{[l]}$;$a^{[l](S)}_{ijk}$ 为激活。
同理,对于生成图像 G,有:
$$G^{[l](G)}_{kk’} = \sum^{n^{[l]}_H}_{i=1} \sum^{n^{[l]}_W}_{j=1} a^{[l](G)}_{ijk} a^{[l](G)}_{ijk’}$$
- 因此,第 $l$ 层的风格代价函数为:
$$J^{[l]}_{style}(S, G) = \frac{1}{(2n^{[l]}_Hn^{[l]}_Wn^{[l]}_C)^2} \sum_k \sum_{k’}(G^{[l](S)}_{kk’} - G^{[l](G)}_{kk’})^2$$
- 如果对各层都使用风格代价函数,效果会更好。因此有:
$$J_{style}(S, G) = \sum_l \lambda^{[l]} J^{[l]}_{style}(S, G)$$
- 其中,$lambda$ 是用于设置不同层所占权重的超参数。
11 一维推广至三维
- 之前我们处理的都是二维图片,实际上卷积也可以延伸到一维和三维数据。我们举两个示例来说明。
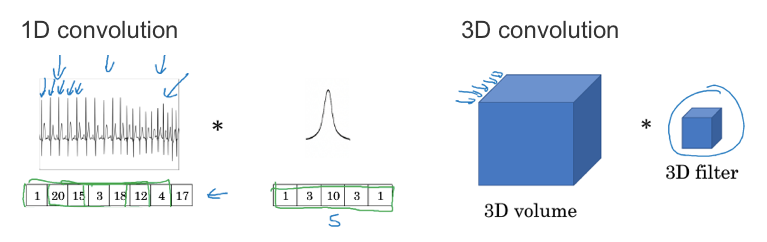
EKG 数据(心电图)是由时间序列对应的每个瞬间的电压组成,是一维数据。一般来说我们会用 RNN(循环神经网络)来处理,不过如果用卷积处理,则有:
- 输入时间序列维度:14 x 1
- 滤波器尺寸:5 x 1,滤波器个数:16
- 输出时间序列维度:10 x 16
而对于三维图片的示例,有
- 输入 3D 图片维度:14 x 14 x 14 x 1
- 滤波器尺寸:5 x 5 x 5 x 1,滤波器个数:16
- 输出 3D 图片维度:10 x 10 x 10 x 16
神经风格迁移的原理没有搞懂,等到下一次学习的时候再深入了解。