02mini-batch梯度下降

# mini-batch优化算法 > 深度学习难以在大数据领域发挥最大效果的一个原因是，在巨大的数据集基础上进行训练速度很慢。而优化算法能够帮助快速训练模型，大大提高效率。 ## 1 mini-batch梯度下降方法 ### batch 梯度下降法 * **batch 梯度下降法**（批梯度下降法，我们之前一直使用的梯度下降法）是最常用的梯度下降形式，即同时处理整个训练集。其在更新参数时使用所有的样本来进行更新。 * 对整个训练集进行梯度下降法的时候，我们必须处理整个训练数据集，然后才能进行一步梯度下降，即每一步梯度下降法需要对整个训练集进行一次处理，如果训练数据集很大的时候，处理速度就会比较慢。 * 但是如果每次处理训练数据的一部分即进行梯度下降法，则我们的算法速度会执行的更快。而处理的这些一小部分训练子集即称为**mini-batch**。 ### Mini-Batch 梯度下降法 * **Mini-Batch 梯度下降法**（小批量梯度下降法）每次同时处理单个的 mini-batch，其他与 batch 梯度下降法一致。 * 使用 batch 梯度下降法，对整个训练集的一次遍历只能做一个梯度下降；而使用 Mini-Batch 梯度下降法，对整个训练集的一次遍历（称为一个 **epoch**）能做 mini-batch 个数个梯度下降。之后，可以一直遍历训练集，直到最后收敛到一个合适的精度。 ### 两者对比 * batch 梯度下降法和 Mini-batch 梯度下降法代价函数的变化趋势如下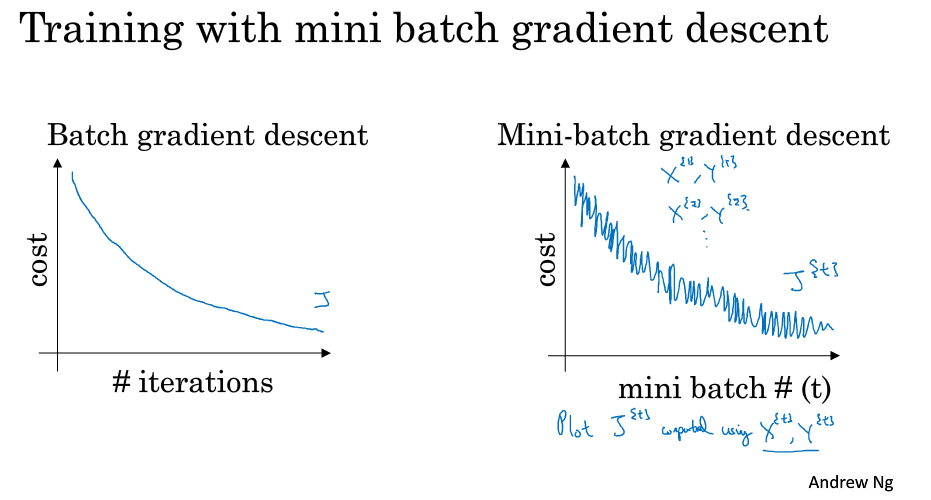：  ### batch-size带来的影响 * mini-batch 的大小为 1，即是**随机梯度下降法（stochastic gradient descent）**，每个样本都是独立的 mini-batch； * mini-batch 的大小为 m（数据集大小），即是 batch 梯度下降法；  * batch 梯度下降法： * 对所有 m 个训练样本执行一次梯度下降，**每一次迭代时间较长，训练过程慢**； * 相对噪声低一些，幅度也大一些； * 成本函数总是向减小的方向下降。 * 随机梯度下降法： * 对每一个训练样本执行一次梯度下降，训练速度快，但**丢失了向量化带来的计算加速**； * 有很多噪声，减小学习率可以适当； * 成本函数总体趋势向全局最小值靠近，但永远不会收敛，而是一直在最小值附近波动。 > 因此，选择一个`1 < size < m`的合适的大小进行 Mini-batch 梯度下降，可以实现快速学习，也应用了向量化带来的好处，且成本函数的下降处于前两者之间。 ### mini-batch 大小的选择 * 如果训练样本的大小比较小，如 m ⩽ 2000 时，选择 batch 梯度下降法； * 如果训练样本的大小比较大，选择 Mini-Batch 梯度下降法。为了和计算机的信息存储方式相适应，代码在 mini-batch 大小为 2 的幂次时运行要快一些。典型的大小为 $2^6$、$2^7$、...、$2^9$； * mini-batch 的大小要符合 CPU/GPU 内存。 > mini-batch 的大小也是一个重要的超变量，需要根据经验快速尝试，找到能够最有效地减少成本函数的值。 ### mini-batch步骤 1. 将数据集打乱； 2. 按照既定的大小分割数据集；

m = X.shape[1] 
permutation = list(np.random.permutation(m))
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((1,m))

* `np.random.permutation`与`np.random.shuffle`有两处不同： 1. 如果传给`permutation`一个矩阵，它会返回一个洗牌后的矩阵副本；而`shuffle`只是对一个矩阵进行洗牌，没有返回值。 2. 如果传入一个整数，它会返回一个洗牌后的`arange`。 ### 符号表示 * 使用上角小括号 i 表示训练集里的值，$x^{(i)}$ 是第 i 个训练样本； * 使用上角中括号 l 表示神经网络的层数，$z^{[l]}$ 表示神经网络中第 l 层的 z 值； * 现在引入大括号 t 来代表不同的 mini-batch，因此有 $X^{t}$、$Y^{t}$。 ## 2 指数平均加权 ### 指数加权平均定义 * **指数加权平均（Exponentially Weight Average）** 是一种常用的序列数据处理方式，计算公式为： $$ S_t = \begin{cases} Y_1, &t = 1 \\\\ \beta S_{t-1} + (1-\beta)Y_t, &t > 1 \end{cases} $$ * 其中 $Y_t$ 为 t 下的实际值，$S_t$ 为 t 下加权平均后的值，β 为权重值。指数加权平均数在统计学中被称为“指数加权移动平均值”。 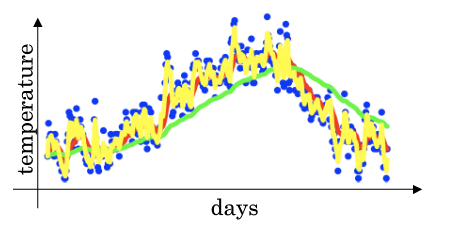 * 给定一个时间序列，例如伦敦一年每天的气温值，图中蓝色的点代表真实数据。对于一个即时的气温值，取权重值 β 为 0.9，根据求得的值可以得到图中的红色曲线，它反映了气温变化的大致趋势。 * 当取权重值 β=0.98 时，可以得到图中更为平滑的绿色曲线。而当取权重值 β=0.5 时，得到图中噪点更多的黄色曲线。**β 越大相当于求取平均利用的天数越多**，曲线自然就会越平滑而且越滞后。 ### 理解指数平均加权 * 当 β 为 0.9 时， $$v_{100} = 0.9v_{99} + 0.1 \theta_{100}$$ $$v_{99} = 0.9v_{98} + 0.1 \theta_{99}$$ $$v_{98} = 0.9v_{97} + 0.1 \theta_{98}$$ $$...$$ $$v_{100} = 0.1 \theta_{100} + 0.1 * 0.9 \theta_{99} + 0.1 * {(0.9)}^2 \theta_{98} + ...$$ * 其中 θi 指第 i 天的实际数据。所有 θ 前面的系数（不包括 0.1）相加起来为 1 或者接近于 1，这些系数被称作**偏差修正（Bias Correction）**。 * 根据函数极限的一条定理： $${\lim_{\beta\to 0}}(1 - \beta)^{\frac{1}{\beta}} = \frac{1}{e} \approx 0.368$$ * 当 β 为 0.9 时，可以当作把过去 10 天的气温指数加权平均作为当日的气温，因为 10 天后权重已经下降到了当天的 1/3 左右。同理，当 β 为 0.98 时，可以把过去 50 天的气温指数加权平均作为当日的气温。因此，在计算当前时刻的平均值时，只需要前一天的平均值和当前时刻的值。 $$v_t = \beta v_{t-1} + (1 - \beta)\theta_t$$ $$v := \beta v + (1 - \beta)\theta_t$$ > 特点：指数平均加权并**不是最精准**的计算平均数的方法，你可以直接计算过去 10 天或 50 天的平均值来得到更好的估计，但缺点是保存数据需要占用更多内存，执行更加复杂，计算成本更加高昂。指数加权平均数公式的好处之一在于它只需要一行代码，且占用极少内存，因此**效率极高，且节省成本**。 ### 指数平均加权的偏差修正 $$v_0 = 0$$ $$v_1 = 0.98v_0 + 0.02\theta_1$$ * $v_1$ 仅为第一个数据的 0.02（或者说 1-β），显然不准确。往后递推同理。因此，我们修改公式为 $$v_t = \frac{\beta v_{t-1} + (1 - \beta)\theta_t}{{1-\beta^t}}$$ * 随着 t 的增大，β 的 t 次方趋近于 0。因此当 t 很大的时候，偏差修正几乎没有作用，但是在前期学习可以帮助更好的预测数据。在实际过程中，一般会忽略前期偏差的影响。 ### 动量梯度下降法 * **动量梯度下降（Gradient Descent with Momentum）** 是计算梯度的指数加权平均数，并利用该值来更新参数值。具体过程为： for l = 1, .. , L： $$v_{dW^{[l]}} = \beta v_{dW^{[l]}} + (1 - \beta) dW^{[l]}$$ $$v_{db^{[l]}} = \beta v_{db^{[l]}} + (1 - \beta) db^{[l]}$$ $$W^{[l]} := W^{[l]} - \alpha v_{dW^{[l]}}$$ $$b^{[l]} := b^{[l]} - \alpha v_{db^{[l]}}$$ * 其中，将动量衰减参数 β 设置为 0.9 是超参数的一个常见且效果不错的选择。当 β 被设置为 0 时，显然就成了 batch 梯度下降法。 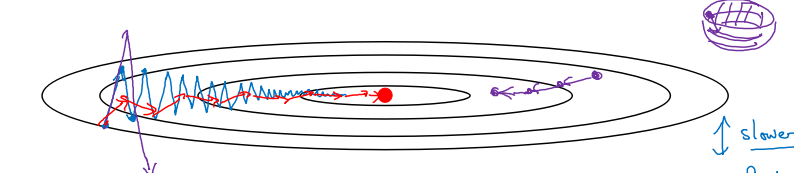 * 进行一般的梯度下降将会得到图中的蓝色曲线，由于存在上下波动，减缓了梯度下降的速度，因此只能使用一个较小的学习率进行迭代。如果用较大的学习率，结果可能会像紫色曲线一样偏离函数的范围。 * 而使用动量梯度下降时，通过累加过去的梯度值来减少抵达最小值路径上的波动，加速了收敛，因此在横轴方向下降得更快，从而得到图中红色的曲线。 * 当前后梯度方向一致时，动量梯度下降能够加速学习；而前后梯度方向不一致时，动量梯度下降能够抑制震荡。 * 另外，在 10 次迭代之后，移动平均已经不再是一个具有偏差的预测。因此实际在使用梯度下降法或者动量梯度下降法时，不会同时进行偏差修正。 ### 动量梯度下降法的形象解释 * 将成本函数想象为一个碗状，从顶部开始运动的小球向下滚，其中 dw，db 想象成球的加速度；而 $v_{dw}$、$v_{db}$ 相当于速度。 * 小球在向下滚动的过程中，因为加速度的存在速度会变快，但是由于 β 的存在，其值小于 1，可以认为是摩擦力，所以球不会无限加速下去。 ## 3 RMSProp 算法 * **RMSProp（Root Mean Square Propagation，均方根传播）** 算法是在对梯度进行指数加权平均的基础上，引入平方和平方根。具体过程为（省略了 l）： $$s_{dw} = \beta s_{dw} + (1 - \beta)(dw)^2$$ $$s_{db} = \beta s_{db} + (1 - \beta)(db)^2$$ $$w := w - \alpha \frac{dw}{\sqrt{s_{dw} + \epsilon}}$$ $$b := b - \alpha \frac{db}{\sqrt{s_{db} + \epsilon}}$$ * 其中，ϵ 是一个实际操作时加上的较小数（例如10^-8），为了防止分母太小而导致的数值不稳定。 * 当 dw 或 db 较大时，$(dw)^2$、$(db)^2$会较大，进而 $s_{dw}$、$s_{db}$也会较大，最终使得梯度变化较小，从而减小某些维度梯度更新波动较大的情况，使下降速度变得更快。 $$\frac{dw}{\sqrt{s_{dw} + \epsilon}}$$ $$\frac{db}{\sqrt{s_{db} + \epsilon}}$$ 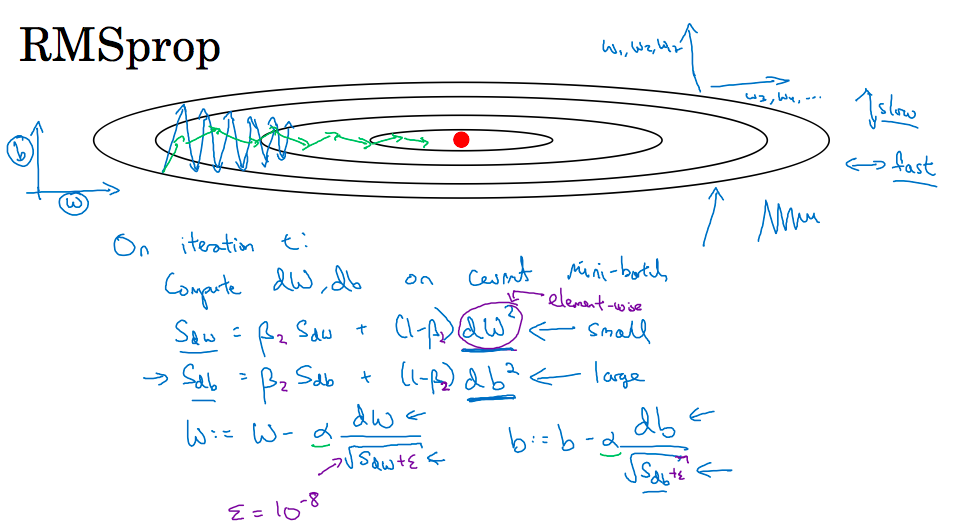 > RMSProp 有助于减少抵达最小值路径上的摆动，并允许使用一个更大的学习率 α，从而加快算法学习速度。并且，它和 Adam 优化算法已被证明适用于不同的深度学习网络结构。注意，β 也是一个超参数。 ## Adam 优化算法 * **Adam 优化算法（Adaptive Moment Estimation，自适应矩估计）** 基本上就是将 Momentum 和 RMSProp 算法结合在一起，通常有超越二者单独时的效果。具体过程如下（省略了 l）： 1. 首先进行初始化 $$v_{dW} = 0, s_{dW} = 0, v_{db} = 0, s_{db} = 0$$ 2. 用每一个 mini-batch 计算 dW、db，第 t 次迭代时： $$v_{dW} = \beta_1 v_{dW} + (1 - \beta_1) dW$$ $$v_{db} = \beta_1 v_{db} + (1 - \beta_1) db$$ $$s_{dW} = \beta_2 s_{dW} + (1 - \beta_2) {(dW)}^2$$ $$s_{db} = \beta_2 s_{db} + (1 - \beta_2) {(db)}^2$$ 3. 一般使用 Adam 算法时需要计算偏差修正： $$v^{corrected}_{dW} = \frac{v_{dW}}{1-{\beta_1}^t}$$ $$v^{corrected}_{db} = \frac{v_{db}}{1-{\beta_1}^t}$$ $$s^{corrected}_{dW} = \frac{s_{dW}}{1-{\beta_2}^t}$$ $$s^{corrected}_{db} = \frac{s_{db}}{1-{\beta_2}^t}$$ 4. 更新 W、b 时有： $$W := W - \alpha \frac{v^{corrected}_{dW}}{{\sqrt{s^{corrected}_{dW}} + \epsilon}}$$ $$b := b - \alpha \frac{v^{corrected}_{db}}{{\sqrt{s^{corrected}_{db}} + \epsilon}}$$ > （可以看到 Andrew 在这里 ϵ 没有写到平方根里去，和他在 RMSProp 中写的不太一样。考虑到 ϵ 所起的作用，我感觉影响不大） ### 超参数的选择 * 学习率 α：需要尝试一系列的值，来寻找比较合适的； * β1：常用的缺省值为 0.9； * β2：Adam 算法的作者建议为 0.999； * ϵ：不重要，不会影响算法表现，Adam 算法的作者建议为 $10^{-8}$； > β1、β2、ϵ 通常不需要调试。 ## 学习率衰减 * 如果设置一个固定的学习率 α，在最小值点附近，由于不同的 batch 中存在一定的噪声，因此不会精确收敛，而是始终在最小值周围一个较大的范围内波动。而如果随着时间慢慢减少学习率 α 的大小，在初期 α 较大时，下降的步长较大，能以较快的速度进行梯度下降；而后期逐步减小 α 的值，即减小步长，有助于算法的收敛，更容易接近最优解。 * 最常用的学习率衰减方法，其中，`decay_rate`为衰减率（超参数），`epoch_num`为将所有的训练样本完整过一遍的次数。 $$\alpha = \frac{1}{1 + decay\\_rate * epoch\\_num} * \alpha_0$$ * 指数衰减： $$\alpha = 0.95^{epoch\\_num} * \alpha_0$$ * 其他： $$\alpha = \frac{k}{\sqrt{epoch\\_num}} * \alpha_0$$ * 离散下降 $$分段函数$$ * 对于较小的模型，也有人会在训练时根据进度手动调小学习率。 ## 局部最优问题 ### 鞍点 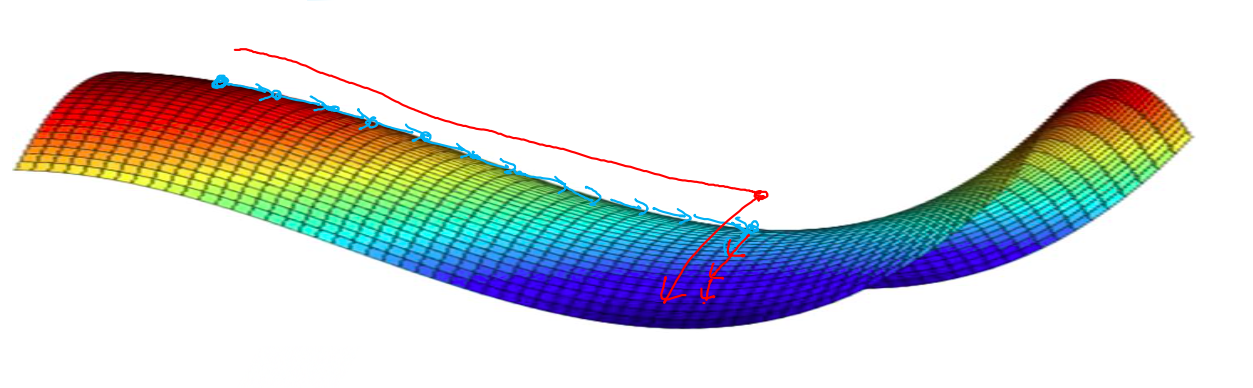 * **鞍点（saddle）** 是函数上的导数为零，但不是轴上局部极值的点。当我们建立一个神经网络时，通常梯度为零的点是上图所示的鞍点，而非局部最小值。减少损失的难度也来自误差曲面中的鞍点，而不是局部最低点。因为在一个具有高维度空间的成本函数中，如果梯度为 0，那么在每个方向，成本函数或是凸函数，或是凹函数。而所有维度均需要是凹函数的概率极小，因此在低维度的局部最优点的情况并不适用于高维度。 ### 结论 * 在训练较大的神经网络、存在大量参数，并且成本函数被定义在较高的维度空间时，困在极差的局部最优中是不大可能的； * 鞍点附近的平稳段会使得学习非常缓慢，而这也是动量梯度下降法、RMSProp 以及 Adam 优化算法能够加速学习的原因，它们能帮助尽早走出平稳段。