浅层神经网络

  • ReLU,recfied linear unit修正线性单元

神经网络表示

  • 竖向堆叠起来的输入特征被称作神经网络的输入层（the input layer）。

  • 神经网络的 隐藏层（a hidden layer） 。“隐藏”的含义是 在训练集中 ，这些中间节点的真正数值是无法看到的。

  • 输出层（the output layer） 负责输出预测值。

  • 下图被称为双层神经网络。包括隐藏层和输出层，一般不考虑输入层。

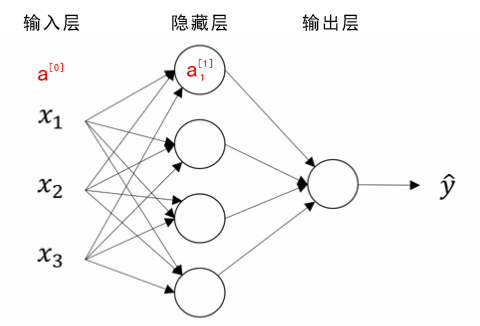
single_hidden_layer_neural_network

  • 如图是一个双层神经网络，也称作单隐层神经网络（a single hidden layer neural network）。当我们计算网络的层数时，通常不考虑输入层，因此图中隐藏层是第一层，输出层是第二层。

约定俗成的符号表示：

  • $x$表示其中一个样本。$a^{0}$第一个样本输入层的激活值。$a^{1}$第一个样本隐藏层产生激活值。
  • $n^{[i]}$表示第i层的单元数量。
  • $z=W^T * a+b$，$x$表示单个样本，$z$表示求和值，$W$权重，$a$上一层产生的激活值，$b$偏置单元。
  • $Z=W^T * A+b$，样本向量化的计算公式，$X$表示多个样本组成的样本矩阵。$A$表示多个样本的样本矩阵的激活值矩阵。$Z$表示求和值得矩阵。
  • $g(z)$ 表示激活函数。
  • 上标[1]表示神经网络第一层。
  • 上标(1)表示训练样本第一个。

计算神经网络的输出

神经网络的计算原理

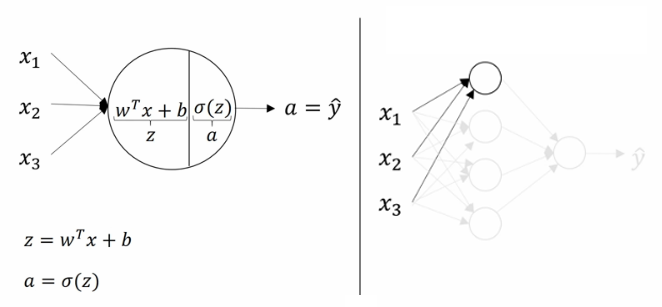
neural_network_like_logistic

神经网络的向量化计算过程

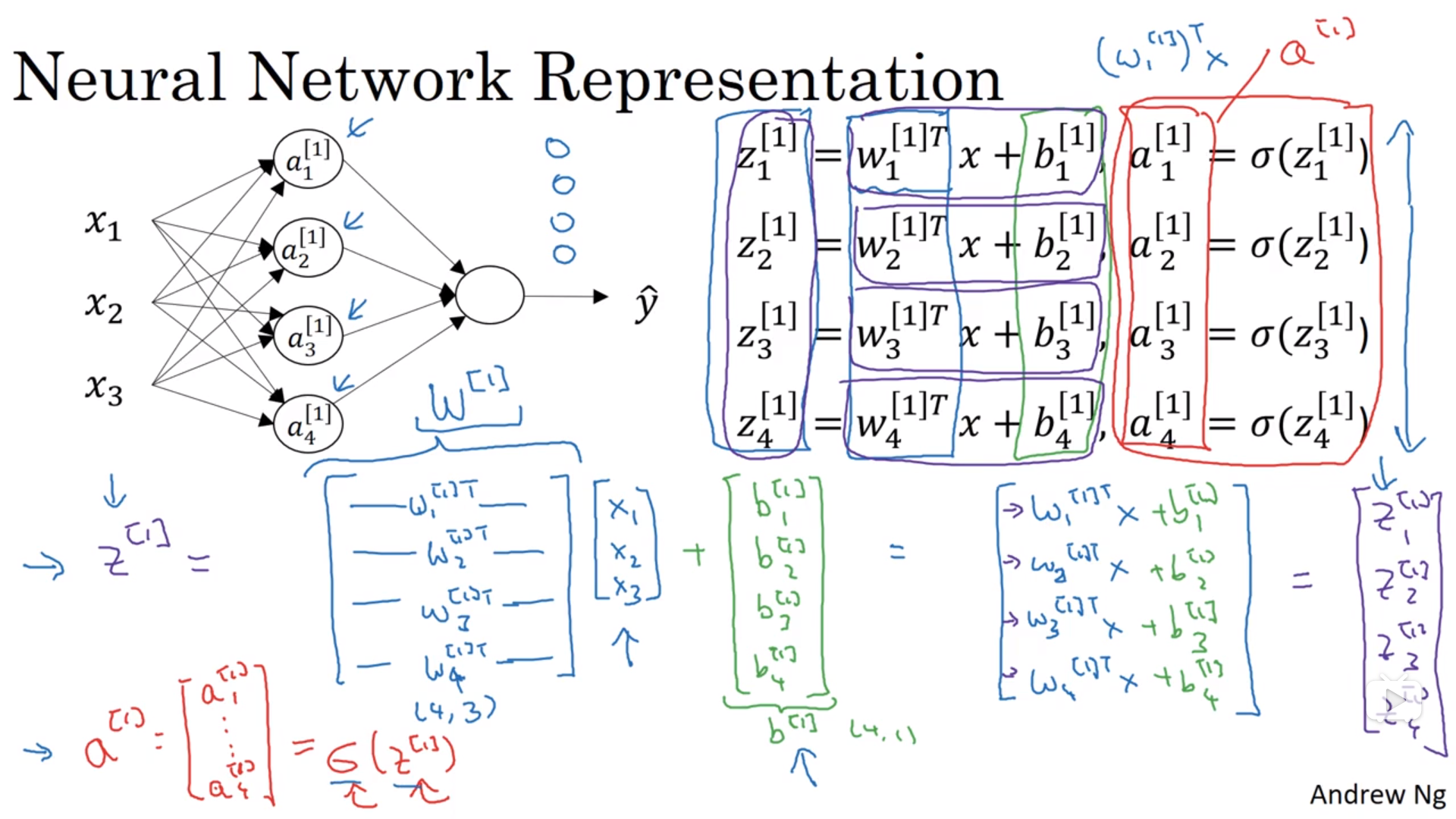
  • 隐藏层计算
    $$z^{[1]} = (W^{[1]})^Ta^{[0]}+b^{[1]}$$

$$a^{[1]} = \sigma(z^{[1]})$$

  • 输出层计算

$$z^{[2]} = (W^{[2]})^Ta^{[1]}+b^{[2]}$$

$$\hat{y} = a^{[2]} = \sigma(z^{[2]})$$

注意事项

  • 输入层和隐藏层之间：${(W^{[1]})}^T$的 shape 为(4,3)，前面的 4 是隐藏层神经元的个数，后面的 3 是输入层神经元的个数；$b^{[1]}$的 shape 为(4,1)，和隐藏层的神经元个数相同。
  • 隐藏层和输出层之间：${(W^{[2]})}^T$的 shape 为(1,4)，前面的 1 是输出层神经元的个数，后面的 4 是隐藏层神经元的个数；$b^{[2]}$的 shape 为(1,1)，和输出层的神经元个数相同。

样本的向量化计算

激活函数

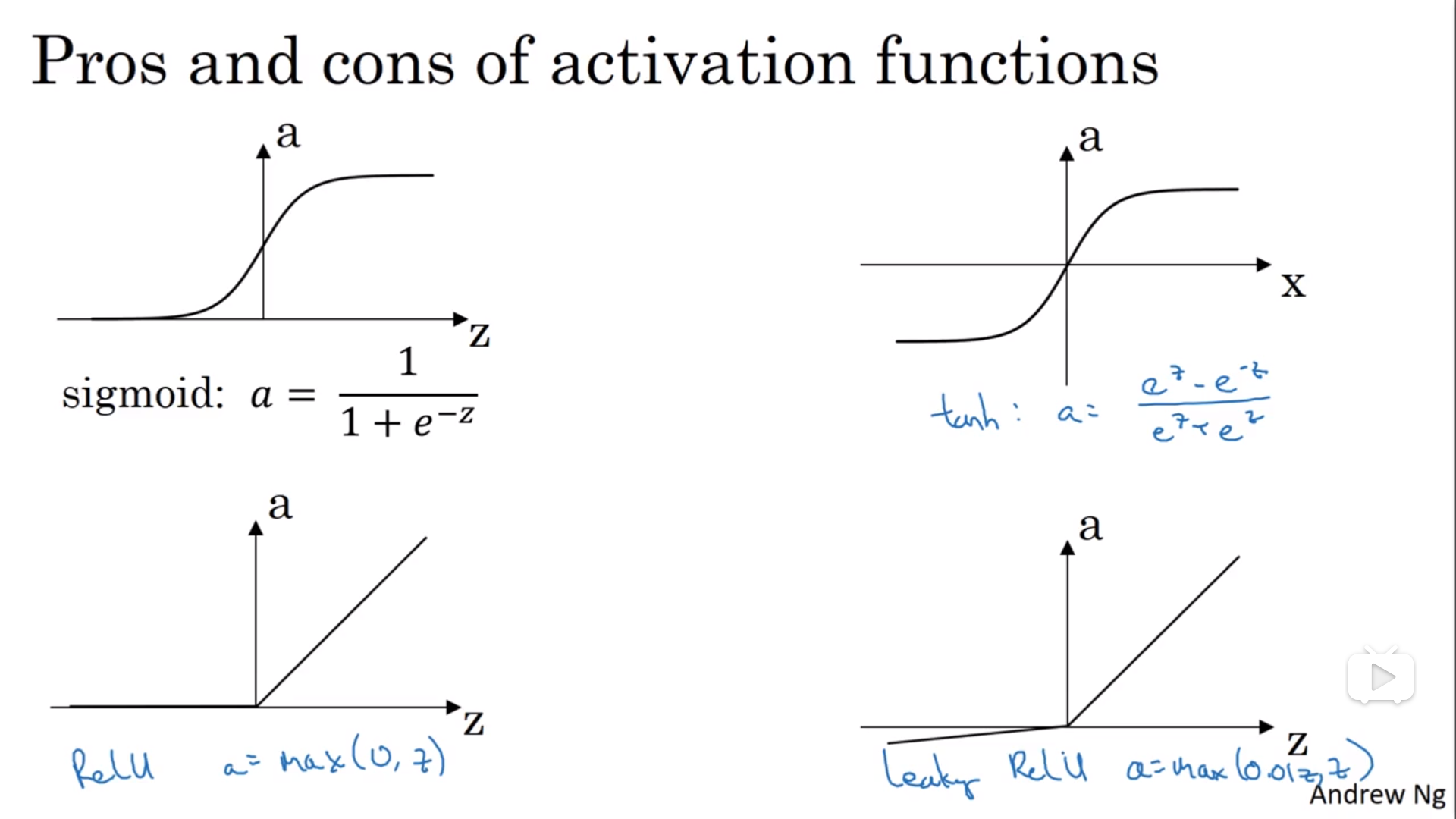
常见激活函数

$$
a = g(z)
$$

  • sigmod函数

$$
a=\frac{1}{1-e^{-z}}
$$

  • tanh 函数（the hyperbolic tangent function，双曲正切函数）

$$a = \frac{e^z - e^{-z}}{e^z + e^{-z}}$$

效果几乎总比 sigmoid 函数好（除开二元分类的输出层，因为我们希望输出的结果介于 0 到 1 之间），因为函数输出介于 -1 和 1 之间，激活函数的平均值就更接近 0，有类似数据中心化的效果。然而，tanh 函数存在和 sigmoid 函数一样的缺点：当 z 趋紧无穷大（或无穷小），导数的梯度（即函数的斜率）就趋紧于 0，这使得梯度算法的速度大大减缓。

  • ReLU 函数（the rectified linear unit，修正线性单元）

$$a=max(0,z)$$

当 z > 0 时，梯度始终为 1，从而提高神经网络基于梯度算法的运算速度，收敛速度远大于 sigmoid 和 tanh。然而当 z < 0 时，梯度一直为 0，但是实际的运用中，该缺陷的影响不是很大。

  • Leaky ReLU（带泄漏的 ReLU）：

$$a=max(0.01z,z)$$

Leaky ReLU 保证在 z < 0 的时候，梯度仍然不为 0。理论上来说，Leaky ReLU 有 ReLU 的所有优点，但在实际操作中没有证明总是好于 ReLU，因此不常用。在选择激活函数的时候，如果在不知道该选什么的时候就选择 ReLU，当然也没有固定答案，要依据实际问题在交叉验证集合中进行验证分析。当然，我们可以在不同层选用不同的激活函数。

使用非线性激活函数的原因

使用线性激活函数和不使用激活函数、直接使用 Logistic 回归没有区别，那么无论神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，就成了最原始的感知器了。

激活函数的导数

  • sigmoid 函数：

$$g(z) = \frac{1}{1+e^{-z}}$$

$$g\prime(z)=\frac{dg(z)}{dz} = \frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})=g(z)(1-g(z))$$

  • tanh 函数：

$$g(z) = tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}$$

$$g\prime(z)=\frac{dg(z)}{dz} = 1-(tanh(z))^2=1-(g(z))^2$$

梯度下降法

正向传播算法

$$Z^{[1]}={(W^{[1]})}^TX+b^{[1]}$$

$$A^{[1]}=g^{[1]}(Z^{[1]})$$

$$Z^{[2]}={(W^{[2]})}^TA^{[1]}+b^{[2]}$$

$$A^{[2]}=g^{[2]}(Z^{[2]})=\sigma(Z^{[2]})$$

反向梯度下降

  • 神经网络反向梯度下降公式（左）和其代码样本向量化（右）：

summary-of-gradient-descent

随机初始化

  • 如果在初始时将两个隐藏神经元的参数设置为相同的大小，那么两个隐藏神经元对输出单元的影响也是相同的，通过反向梯度下降去进行计算的时候，会得到同样的梯度大小，所以在经过多次迭代后，两个隐藏层单位仍然是对称的。无论设置多少个隐藏单元，其最终的影响都是相同的，那么多个隐藏神经元就没有了意义。

  • 在初始化的时候，W 参数要进行随机初始化，不可以设置为 0。而 b 因为不存在对称性的问题，可以设置为 0。以 2 个输入，2 个隐藏神经元为例：

1
2
W = np.random.rand(2,2)* 0.01
b = np.zeros((2,1))

  • 这里将 W 的值乘以 0.01（或者其他的常数值）的原因是为了使得权重 W 初始化为较小的值，这是因为使用 sigmoid 函数或者 tanh 函数作为激活函数时，W 比较小，则 Z=WX+b 所得的值趋近于 0，梯度较大，能够提高算法的更新速度。而如果 W 设置的太大的话，得到的梯度较小，训练过程因此会变得很慢。

  • ReLU 和 Leaky ReLU 作为激活函数时不存在这种问题，因为在大于 0 的时候，梯度均为 1。