03深层神经网络
深层神经网络
深层神经网络的符号表示
- $L=4$,神经网络有四层。
- $n^{[l]}$,l层上单元的个数。
- $a^{[l]}$,l层上激活函数的输出,激活值。
- x表示输入的特征。
- $a^{[l]}g^{[l]}(z^{[l]})$l层的激活函数
- $z^{[l]}=W^{[l]T}a^{[l-1]}+b^{[l]}$,l层的求和
深层网络中的前向和反向传播
前向传播
输入:$a^{[l−1]}$
输出:$a^{[l]}$,cache($z^{[l]}$)
公式:
$$Z^{[l]}=W^{[l]}\cdot a^{[l-1]}+b^{[l]}$$
$$a^{[l]}=g^{[l]}(Z^{[l]})$$
反向传播
输入:$da^{[l]}$
输出:$da^{[l-1]}$,$dW^{[l]}$,$db^{[l]}$
公式:
$$dZ^{[l]}=da^{[l]}*g^{[l]}{‘}(Z^{[l]})$$
$$dW^{[l]}=dZ^{[l]}\cdot a^{[l-1]}$$
$$db^{[l]}=dZ^{[l]}$$
$$da^{[l-1]}=W^{[l]T}\cdot dZ^{[l]}$$
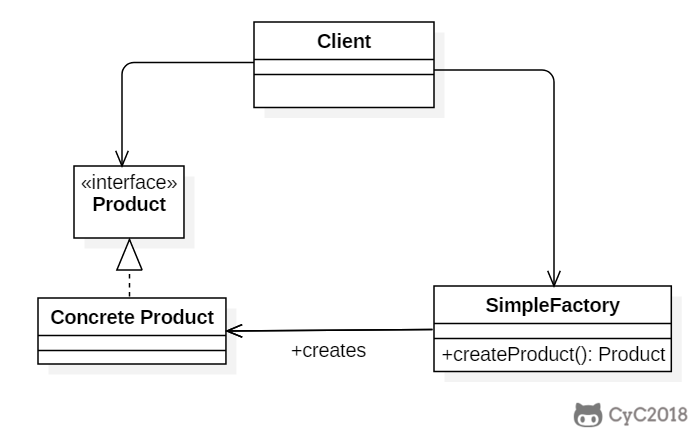
搭建深层神经网络块
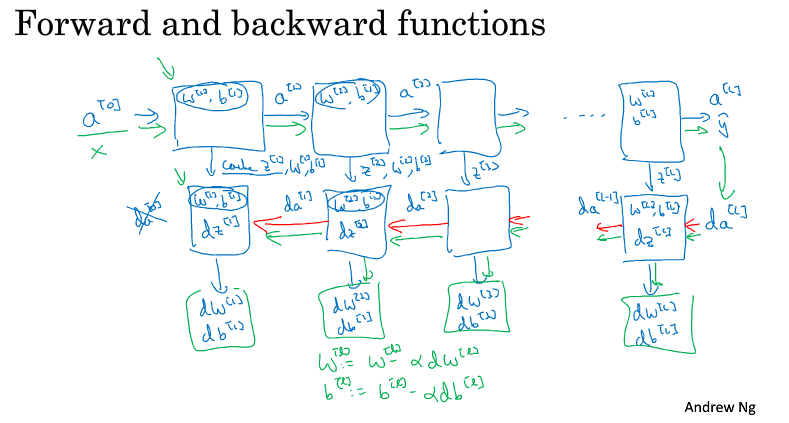
神经网络的一步训练(一个梯度下降循环),包含了从 $a^{[0]}$(即 x)经过一系列正向传播计算得到 $\hat y$ (即 $a^{[l]}$)。然后再计算 $da^{[l]}$,开始实现反向传播,用链式法则得到所有的导数项,W 和 b 也会在每一层被更新。
在代码实现时,可以将正向传播过程中计算出来的 z 值缓存下来,待到反向传播计算时使用。
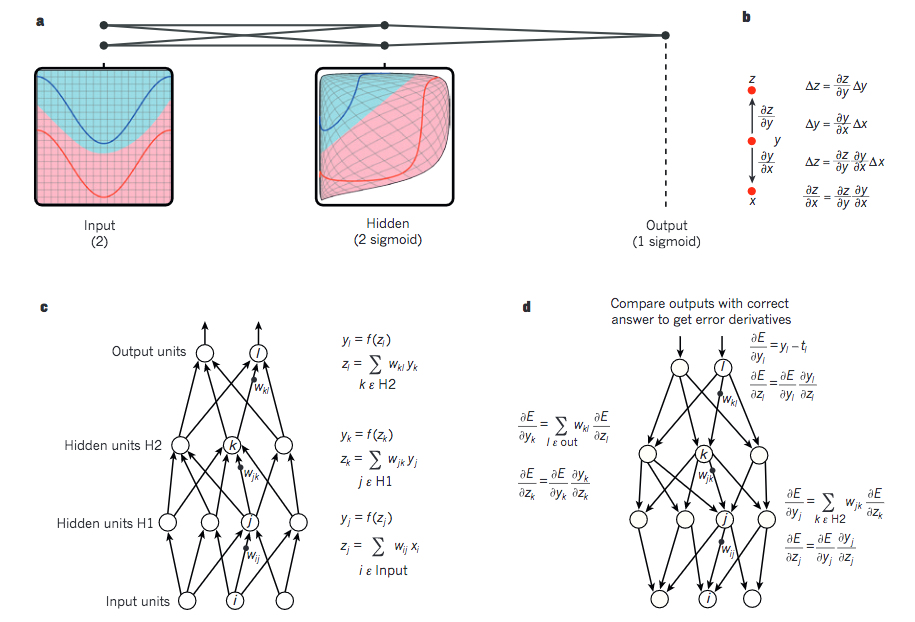
补充一张从 Hinton、LeCun 和 Bengio 写的深度学习综述中摘下来的图,有助于理解整个过程:
矩阵的维度核对
$$W^{[l]}: (n^{[l]}, n^{[l-1]})$$
$$b^{[l]}: (n^{[l]}, 1)$$
$$dW^{[l]}: (n^{[l]}, n^{[l-1]})$$
$$db^{[l]}: (n^{[l]}, 1)$$
对于 Z、a,向量化之前有:
$$Z^{[l]}, a^{[l]}: (n^{[l]}, 1)$$
而在向量化之后,则有:
$$Z^{[l]}, A^{[l]}: (n^{[l]}, m)$$
在计算反向传播时,dZ、dA 的维度和 Z、A 是一样的。
使用深层表示的原因
对于人脸识别,神经网络的第一层从原始图片中提取人脸的轮廓和边缘,每个神经元学习到不同边缘的信息;网络的第二层将第一层学得的边缘信息组合起来,形成人脸的一些局部的特征,例如眼睛、嘴巴等;后面的几层逐步将上一层的特征组合起来,形成人脸的模样。随着神经网络层数的增加,特征也从原来的边缘逐步扩展为人脸的整体,由整体到局部,由简单到复杂。层数越多,那么模型学习的效果也就越精确。
同样的,对于语音识别,第一层神经网络可以学习到语言发音的一些音调,后面更深层次的网络可以检测到基本的音素,再到单词信息,逐渐加深可以学到短语、句子。
通过例子可以看到,随着神经网络的深度加深,模型能学习到更加复杂的问题,功能也更加强大。
参数和超参数
- 参数即是我们在过程中想要模型学习到的信息(模型自己能计算出来的),例如 $W^{[l]}$,$b^{[l]}$。属于模型本身的一部分。
- 超参数(hyper parameters) 即为控制参数的输出值的一些网络信息(需要人经验判断)。超参数的改变会导致最终得到的参数 $W^{[l]}$,$b^{[l]}$ 的改变。超参数是训练过程相关的参数,用于训练模型的参数,不属于模型,属于训练过程。
典型的超参数有:
- 学习速率:α
- 迭代次数:N
- 隐藏层的层数:L
- 每一层的神经元个数:$n^{[1]}$,$n^{[2]}$,…
- 激活函数 g(z) 的选择
当开发新应用时,预先很难准确知道超参数的最优值应该是什么。因此,通常需要尝试很多不同的值。应用深度学习领域是一个很大程度基于经验的过程。