readme
发表于|更新于|机器学习
|总字数:55|阅读时长:1分钟|浏览量:
这里主要以各种算法的理论知识为主进行说明。
从算法的角度,进行说明。(算法角度的理论总结)
算法相关的项目的实现。(机器学习实战)
文章作者: Estom
版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Estom的博客!
相关推荐

2021-03-08
6. 软件架构模式
软件机构模式1 基于构件的软件架构模式2 软件架构的多视图3 软件架构模式4 接口设计1 软件架构1.1 定义 一个程序或计算机系统的软件架构是包含了该系统的软件元素、这些元素的外部可见的属性以及这些元素之间关系的结构或一组系统结构 描述角度:静态和动态;动能和非功能的。 1.2 基于构件的软件架构 软件由构件组成,每个组件相对独立的封装了一些信息。 构件可以由简单对象或由其他对象组成的复合对象。 构件通过接口与其他对象通信。(接口描述了通信所需要的信息,接口与实现分离,接口约定了通信模式) 1.3 设计方式 顺序式设计:没有控制线程的被动类。把构件单独编译存储在构件库中,通过调用-返回的方式进行通信。(只有一个主动类) 并发或分布式设计:构件是主动地,可以被部署到一个分布式环境的不同节点上,并发构件可以通过几种不同的通信模式进行通信:同步模式、异步模式、代理模式,群组通信模式。 2 软件架构的多视图2.1 视图角度 结构视图:是一种静态视图,使用类图来描述。 动态视图:是一种行为视图,使用通信图来描述。 部署视图:软件架构的物理配置,子系统如何在一个分布的配置中,分配到不...

2022-12-05
30.如何保证接口的幂等性常见的实现方案有哪些
如何保证接口的幂等性?常见的实现方案有哪些?幂等性问题是面试中常见的面试问题,也是分布式系统最常遇到的问题之一。在说幂等性之前,我们先来看一种情况,假如老王在某电商平台进行购物,付款的时候不小心手抖了一下,连续点击了两次支付,但此时服务器没做任何验证,于是老王账户里面的钱被扣了两次,这显然对当事人造成了一定的经济损失,并且还会让用户丧失对平台的信任。而幂等性问题说的就是如何防止接口的重复无效请求。 我们本课时的面试题是,什么是幂等性?如何保证接口的幂等性? 典型回答幂等性最早是数学里面的一个概念,后来被用于计算机领域,用于表示任意多次请求均与一次请求执行的结果相同,也就是说对于一个接口而言,无论调用了多少次,最终得到的结果都是一样的。比如以下代码: 12345678910111213141516public class IdempotentExample { // 变量 private static int count = 0; /** * 非幂等性方法 */ public static void addCount() {...

2021-03-08
5 软件文档评审
为什么要评审提高项目的生产率,减少开发时间,加快开发进度。改善软件质量,改进开发过程。在评审过程中,使开发团队的其他成员更熟悉产品和开发过程。通过评审,标志着软件开发的一个阶段的完成。生产出更以维护的软件。 参与评审的角色评审组长评审的组织者,确保评审入口准则得到满足确保遵循评审的流程,指明评审的关注点,确保所有评审软院已经充分检视。确保评审的进度,确保发现、整理、修正问题。宣读员在评审会议上通过讲解来引导评审团队浏览工作产品记录员记录会议上的信息作者确保工作产品已经准备好,在评审会议上详解工作产品。在评审会议结束后修改所有已经确认的缺陷。评审员寻找被评审工作产品中的缺陷,填写评审表单并上交。参加评审会议,就评审出的缺陷提出建设性建议。 评审的内容管理评审——组织的最高管理者就管理体系就现状、适宜性、充分性和有效性以及方针和目标的贯彻落实及实现情况进行正式的评价。技术评审——发现软件在功能、逻辑、实现上的错误,验证软件符合他的需求规格。确认软件符合预先定义的开发规范和标准。保证软件在同一模式下进行开发。过程评审——评估主要的质量保证流程;卡利率如何处理和解决评审过程中发现的不符合...

2021-03-09
Dijkstra 单源最短路径算法
Dijkstra 单源最短路径算法 Dijkstra 算法是一种用于计算带权有向图中单源最短路径(SSSP:Single-SourceShortest Path)的算法,由计算机科学家 Edsger Dijkstra 于 1956 年构思并于 1959年发表。其解决的问题是:给定图 G 和源顶点 v,找到从 v 至图中所有顶点的最短路径。 Dijkstra 算法采用贪心算法(GreedyAlgorithm)范式进行设计。在最短路径问题中,对于带权有向图 G = (V, E),Dijkstra算法的初始实现版本未使用最小优先队列实现,其时间复杂度为 O(V2),基于 Fibonacciheap的最小优先队列实现版本,其时间复杂度为 O(E + VlogV)。 Bellman-Ford算法和Dijkstra算法同为解决单源最短路径的算法。对于带权有向图G = (V, E),Dijkstra 算法要求图 G 中边的权值均为非负,而 Bellman-Ford算法能适应一般的情况(即存在负权边的情况)。一个实现的很好的 Dijkstra 算法比Bellman-For...
2024-01-07
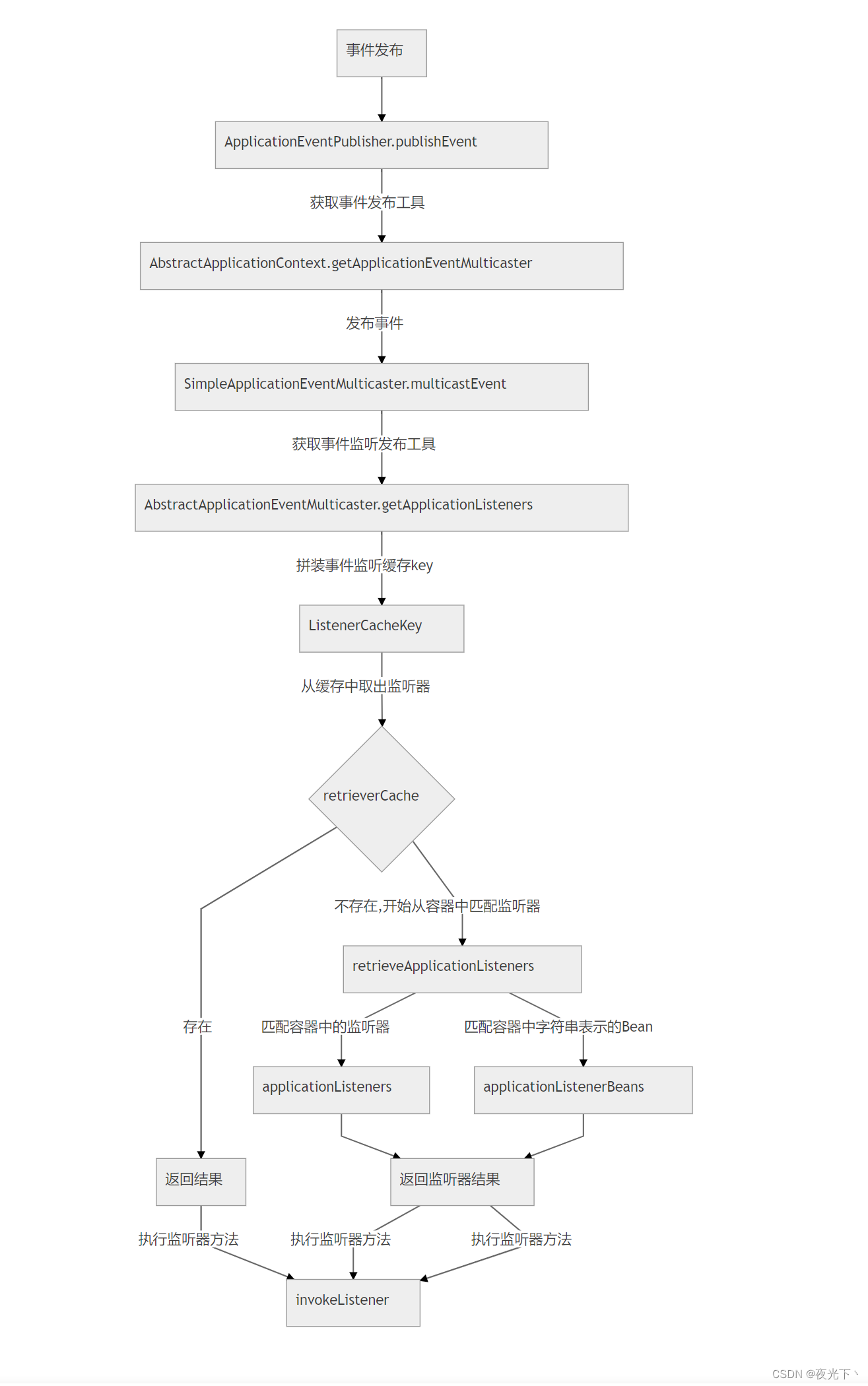
5.9 订阅发布模式(事件驱动)
事件驱动和订阅发布模式1 事件驱动/订阅发布模式 参考文献:https://blog.csdn.net/weixin_46058921/article/details/126978976 简介事件驱动一个常见的形式就是 发布-订阅 模式,在跨进程的通信间,我们常常使用 消息队列 来实现消息的发布订阅。目前主流的框架中,均采用消息的 发布-订阅 模式来进行大型分布式项目的解耦。使得数据生产方和发送方分离,同时 MQ 还能起到削峰的作用。同一进程内很多时候也需要这种事件驱动机制来进行解耦 原理事件机制主要由三个部分组成:事件源、事件对象、监听器 事件源(订阅发布模式中的发布者):事件发生的起源 事件对象(观察者模式中的主题):事件实体,事件对象会持有一个事件源 监听器(观察者模式中的观察者、订阅发布模式中的订阅者):监听事件对象,对事件对象进行处理 事件分发器(复杂事件模型中负责将将事件源发出的时间触发订阅者的行为,决定了是同步行为还是异步行为) 2 Java事件驱动Java 提供了关于事件相关的两个接口: EventObject:事件对象,自定义事件需要继承该类 ...

2021-09-02
03-日志记录
概述上篇文章分享了 Gin 框架的路由配置,这篇文章分享日志记录。 查了很多资料,Go 的日志记录用的最多的还是 github.com/sirupsen/logrus。 Logrus is a structured logger for Go (golang), completely API compatible with the standard library logger. Gin 框架的日志默认只会在控制台输出,咱们利用 Logrus 封装一个中间件,将日志记录到文件中。 这篇文章就是学习和使用 Logrus 。 日志格式比如,我们约定日志格式为 Text,包含字段如下: 请求时间、日志级别、状态码、执行时间、请求IP、请求方式、请求路由。 接下来,咱们利用 Logrus 实现它。 Logrus 使用用 dep 方式进行安装。 在 Gopkg.toml 文件新增: 123[[constraint]] name = "github.com/sirupsen/logrus" version = "1.4.2" 在项目中导入: ...
公告
欢迎参观Estom的小屋




