数组

1 数组的简介

定义

数组是存储在连续内存位置的相同类型数据项的集合，是最简单的线性数据结构。
- 数组的每个数据元素都可以使用下表索引运算符，进行随机访问。
- 数组可以有一个或多个维度。
- 每个元素具有相同的数据类型并且具有相同的大小，即int = 4个字节。

1
2
3

int arr[10];
char arr[10]; 
float arr[5];

优点

数组为同一类型的变量组提供单一名称，因此很容易记住数组中所有元素的名称。
遍历数组是一个非常简单的过程，只需要递增数组的基址，就可以逐个访问每个元素。
可以使用索引直接访问数组中的任何元素。

时间复杂性

算法	平均情况	最坏情况
访问	O(1)	O(1)
搜索	O(n)	O(n)
插入	O(n)	O(n)
删除	O(n)	O(n)

空间复杂性

在数组中，最坏情况下的空间复杂度是O(n)。

2 数组的类型

一维数组

一维（或单维）数组是一种线性数组，其中元素的访问是以行或列索引的单一下标表示。
C++ 将高维维数组存储为一维数组。因此，如果我们将 A 定义为也包含 M * N 个元素的二维数组，那么实际上 A[i][j] 就等于 A[i * N + j]。

多维数组

普通数组采用一个整数来作下标。多维数组（高维数组）的概念特别是在数值计算和图形应用方面非常有用。我们在多维数组之中采用一系列有序的整数来标注，如在[ 3,1,5 ] 。这种整数列表之中整数的个数始终相同，且被称为数组的“维度”。关于每个数组维度的边界称为“维”。维度为 k 的数组通常被称为 k 维。
多维数组的数组名字，在表达式中自动转换为数组首元素地址值，但这个首元素实际上是去除数组下标第一维之后的数组剩余部分。

3 数组的存储和实现

数组存储

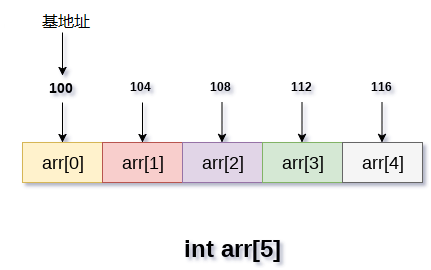
数组的所有数据元素都存储在主存储器中的连续位置。
数组名称表示主存储器中的基地址或第一个元素的地址。
数组的每个元素都由适当的索引表示。可以用三种方式定义数组的索引。
- 0(从零开始索引)：数组的第一个元素是arr[0]。
- 1(基于一个索引)：数组的第一个元素是arr [1]。
- n(基于n的索引)：基于数组的第一个元素，可以定位任何随机索引值。

数组实现

C++内置数组数据类型。

1 2	int a[4]; double b[3][9];//内置数组

STL提供两种灵活的数组结构。

1 2	array<int, 5> arr = {1, 2, 3, 4, 5};//STL模板数组 vector<int> vec ={3,4,3};//STL模板向量，可变长度的数组

4 数组的操作

基础操作

创建
遍历
插入
删除

创建

// 定义数组
int size =20;//容量
int numbers =10;//数据量
int a[20]={1,3,4,5,6,7,4,2,4,5};

遍历

// 数组遍历
for(int i=0;i<10;i++){
    cout<<a[i];
}

插入

//数组插入,尾插入
int value=9;
if(numbers<size){
    a[numbers]=value;
    numbers++;
}
else{
    cout<<"overflow"<<endl;
}
// 数组插入，头插入
int value=10;
if(numbers<size){
    for(int i=1;i<=numbers,i++){
        a[numbers]=a[numbers-i];
    }
    a[0]=value;
}
else{
    cout<<"overflow"<<endl;
}

删除

// 删除
int aim=8;
if(aim>=numbers){
    cout<<"overbound"<<endl;
}
else{
    for(int i=aim;i<numbers-1;i++){
        a[i]=a[i+1];
    }
}

5 二维数组(矩阵)

二维数组的表示

二维数组的大小等于行数和数组中存在的列数的乘积。
一般将二维数组映射到一维数组，存储在内存中。
- 一个3 X 3的二维数组如下图所示。需要将此数组映射到一维数组，存储到内存中。

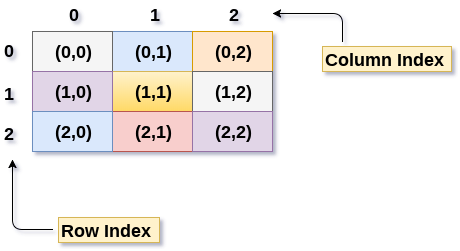
二维数组的存储——行主顺序

在行主排序中，二维数组的所有行连续地存储在存储器中。上图中所示数组，它按行主顺序的存储器分配如下所示

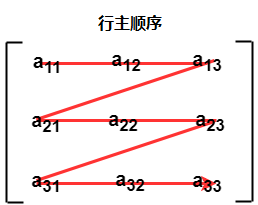
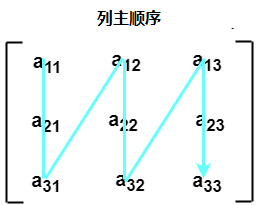
二维数组的存储——列主顺序

根据列主排序，二维数组的所有列都连续地存储在存储器中。上面图像中所示数组的存储器分配给出如下

计算二维数组随机元素的地址

由于存在两种不同的将二维数组存储到存储器中的技术，因此也有两种不同的公式来计算二维数组的随机元素的地址。
- 按行主顺序如果数组由a[m][n]声明，其中m是行数，而n是列数，则以行主顺序存储的数组的元素a[i][j]的地址计算为

1	Address(a[i][j]) = B. A. + (i * n + j) * size

按列主顺序如果数组由a[m][n]声明，其中m是行数，而n是列数，则以列主顺序存储的数组的元素a[i][j]的地址计算为，

1	Address(a[i][j]) = ((jm)+i)Size + BA