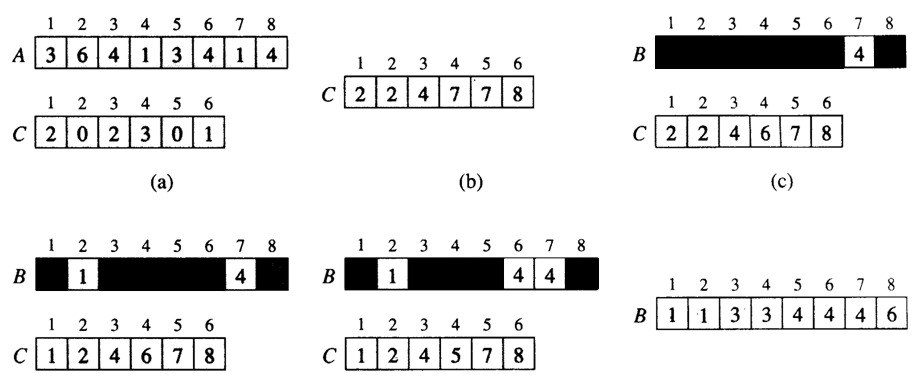
1 重复数字问题

问题描述

  • 找出数组中重复的数字。在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
  • 问题链接

问题分析

  • 重复问题的解决大部分都可以使用哈希表。然后根据元素提供的额外属性采用哈希表的变种。
  • 如本题中提供了额外的限制——0-n-1范围内的数字。那么除了用提供的unordered_set。也可以使用数组作为哈希表，数组的下标作为键，数组的值为值。于是很容易想到第二种方法的改进，即第三种方法。

问题分类

  • 线性数据结构
  • 查找问题
  • 枚举法。

1.1 重复数字问题——排序

策略选择

算法设计

  • 使用快速排序
  • 寻找第一组相邻的重复数字。

正确性证明

算法分析

  • 时间复杂度O(nlogn)
  • 空间复杂度O(logn)

算法实现

1
2
3
4
5
6
7
8
9
10
// 排序方法。排序后出现连续重复数字。
int findRepeatNumber1(vector<int>& nums) {
    sort(nums.begin(),nums.end());
    for(int i=0;i<nums.size()-1;i++){
        if(nums[i]==nums[i+1]){
            return(nums[i]);
        }
    }
    return 0;
}

1.2 重复数字问题——hashset

策略选择

  • 数据结构：哈希表散列表
  • 算法思想：枚举法

算法设计

  • 使用unordered_set已有的元素。
  • 依次检验每一个元素。set中没有元素则保存。有元素则重复

算法分析

  • 时间复杂度O(n)
  • 空间复杂度O(n)

算法实现

1
2
3
4
5
6
7
8
9
10
11
// hashset的方法
int findRepeatNumber2(vector<int>& nums) {
    unordered_set<int> m;
    for(int i=0;i<nums.size();i++){
        if(m.count(nums[i])>0){
            return(nums[i]);
        }
        m.insert(nums[i]);
    }
    return 0;
}

1.3 重复数字问题——原地置换

策略选择

  • 数据结构：数组哈希表
  • 算法思想：枚举法线性查找

算法设计

  • 利用数组的下标作为键。每次将元素归位。
  • 如果数组下标与元素值相等。则下一个
  • 如果数组下边与元素值不想等，则一直交换本元素值。直到相等
  • 如果要交换的两个元素值相等。则检测到重复元素。返回

算法分析

  • 时间复杂度O(n)
  • 空间复杂度O(1)

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
// 原地置换的方法
 int findRepeatNumber(vector<int>& nums) {
     for(int i=0;i<nums.size();i++){
         if(i==nums[i])continue;
         if(nums[i]==nums[nums[i]])return nums[i];
         else {
             swap(nums[i],nums[nums[i]]);
             i--;
         }
     }
     return 0;
 }

2 数组中超过一半的数

问题描述

  • 数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。你可以假设数组是非空的，并且给定的数组总是存在多数元素。
  • 链接

问题分析

问题分类

策略选择

  • 数论知识补充
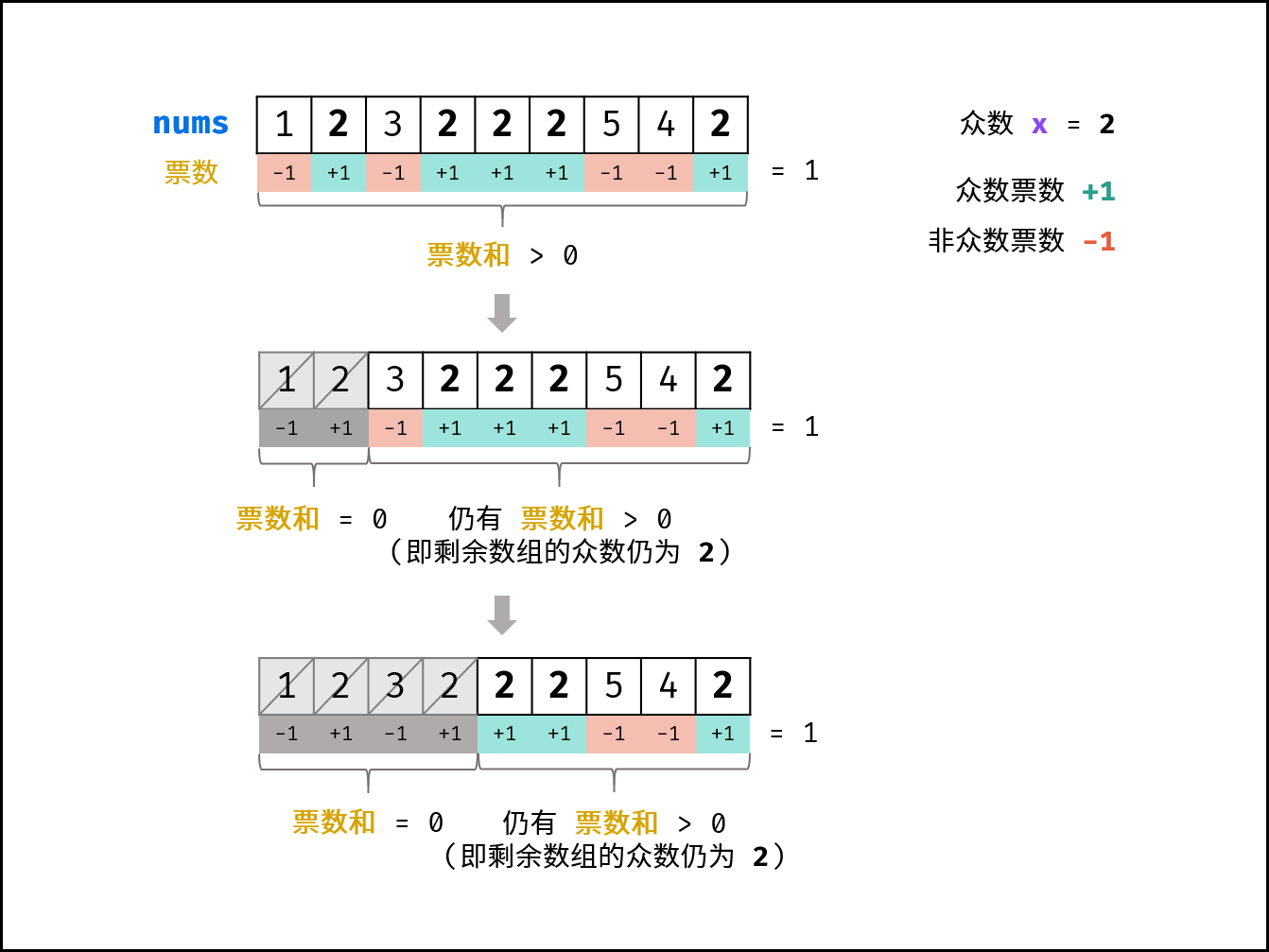
  • 推论一： 若记 众数 的票数为 +1+，非众数 的票数为 -1 ，则一定有所有数字的 票数和 > 0 。
  • 推论二： 若数组的前 a 个数字的 票数和 =0 ，则 数组剩余 (n−a) 个数字的 票数和一定仍 >0 ，即后 (n−a) 个数字的 众数仍为 x

算法设计

  • 摩尔投票法
    1. 初始化： 票数统计 votes = 0 ， 众数 x；
    2. 循环： 遍历数组 nums 中的每个数字 num ；
      1. 当 票数 votes 等于 0 ，则假设当前数字 num 是众数；
      2. 当 num = x 时，票数 votes 自增 1 ；当 num != x 时，票数 votes 自减 1 ；
    3. 返回值： 返回 x 即可；

算法分析

  • 时间复杂度 O(N) ： N 为数组 nums 长度。
  • 空间复杂度 O(1)： votes 变量使用常数大小的额外空间。

算法实现

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int x = 0, votes = 0;
        for(int num : nums){
            if(votes == 0) x = num;
            votes += num == x ? 1 : -1;
        }
        return x;
    }
};

3 数组中数字出现的次数I

问题描述

  • 一个整型数组 nums 里除两个数字之外，其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n)，空间复杂度是O(1)。
  • 示例 1：
1
2
输入：nums = [4,1,4,6]
输出：[1,6] 或 [6,1]

问题分析

  • 问题类别：重复查找问题

策略选择

  • 数据结构：线性数据结构
  • 算法思想：位运算

算法设计

  • 如果除了一个数字以外，其他数字都出现了两次，那么如何找到出现一次的数字？

  • 答案很简单：全员进行异或操作即可。考虑异或操作的性质：对于两个操作数的每一位，相同结果为 00，不同结果为 11。那么在计算过程中，成对出现的数字的所有位会两两抵消为 00，最终得到的结果就是那个出现了一次的数字。

  • 如果有两位一样

  • 先对所有数字进行一次异或，得到两个出现一次的数字的异或值。

  • 在异或结果中找到任意为 1的位.

  • 根据这一位对所有的数字进行分组。

  • 在每个组内进行异或操作，得到两个数字。

算法分析

  • 时间复杂度：O(n)，我们只需要遍历数组两次
  • 空间复杂度：O(1)，只需要常数的空间存放若干变量。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<int> singleNumbers(vector<int>& nums) {
        int ret = 0;
        for (int n : nums)
            ret ^= n;
        int div = 1;
        while ((div & ret) == 0)
            div <<= 1;
        //可以优化while循环
        //div = n & ((~n)-1)//lowbit()运算保留最后一位1
        int a = 0, b = 0;
        for (int n : nums)
            if (div & n)
                a ^= n;
            else
                b ^= n;
        return vector<int>{a, b};
    }
};

4 数组中数字出现的次数II

问题描述

在一个数组 nums 中除一个数字只出现一次之外，其他数字都出现了三次。请找出那个只出现一次的数字。

  • 示例 1：
1
2
输入：nums = [3,4,3,3]
输出：4

问题分析

  • 问题分类：查找重复
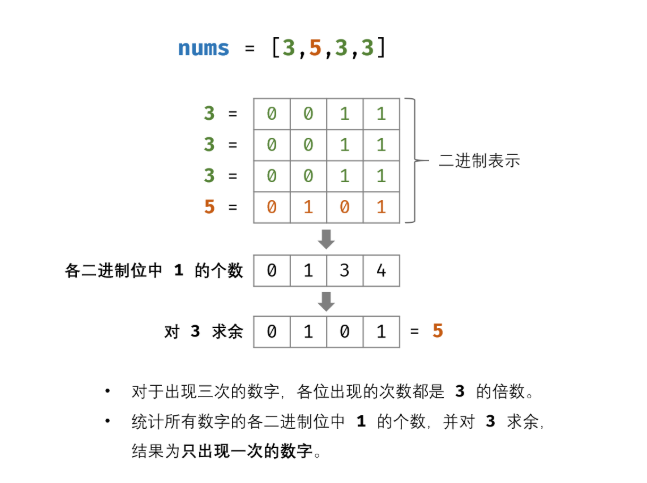
  • 问题抽象：如下图所示，考虑数字的二进制形式，对于出现三次的数字，各 二进制位 出现的次数都是 33 的倍数。因此，统计所有数字的各二进制位中 11 的出现次数，并对 33 求余，结果则为只出现一次的数字

策略选择

  • 算法思想：变治法

算法设计

  • 使用 与运算 ，可获取二进制数字 num 的最右一位$n_1$ $n_1 = num & 1$
  • 配合 无符号右移操作 ，可获取 num 所有位的$n_1$ $num = num >> 1$
  • 建立一个长度为 32 的数组 countscounts ，通过以上方法可记录所有数字的各二进制位的 11 的出现次数。
  • 将 countscounts 各元素对 33 求余，则结果为 “只出现一次的数字” 的各二进制位。

算法分析

  • 时间复杂度 O(N)
  • 空间复杂度 O(1)

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int singleNumber(int[] nums) {
        int[] counts = new int[32];
        for(int num : nums) {
            for(int j = 0; j < 32; j++) {
                counts[j] += num & 1;
                num >>>= 1;
            }
        }
        int res = 0, m = 3;
        for(int i = 0; i < 32; i++) {
            res <<= 1;
            res |= counts[31 - i] % m;
        }
        return res;
    }
}