动态规划——线性动态规划

主要用来熟练动态规划的步骤

  • 斐波那契数列
  • 青蛙跳台阶
  • 最大子段和

1 斐波那契数列

问题描述

  • 写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：
1
2
F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
  • 斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。
  • 链接

问题分析

问题分类

  • 数组
  • 动态规划+迭代

选择策略

  • 数组
  • 动态规划
    • 原理： 以斐波那契数列性质f(n+1)=f(n)+f(n−1) 为转移方程。

算法设计

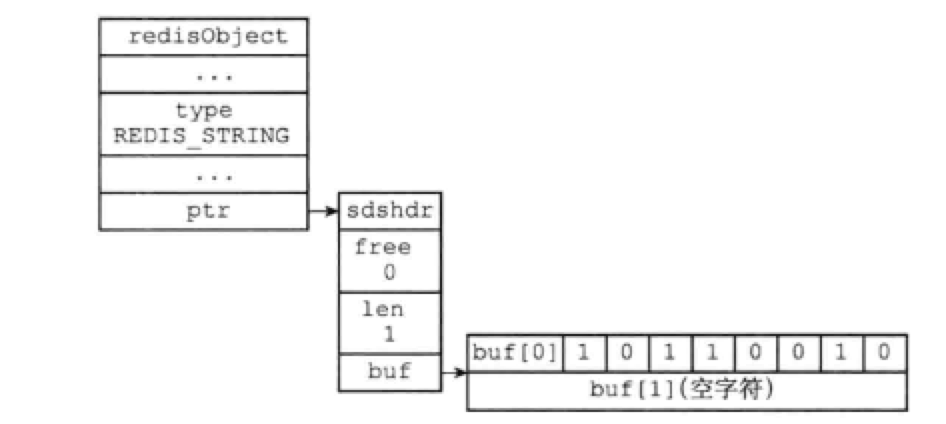
  • 状态定义： 设$dp$为一维数组，其中 $dp[i]$ 的值代表 斐波那契数列第 $i$个数字 。
  • 转移方程： $dp[i + 1] = dp[i] + dp[i - 1]$，即对应数列定义 $f(n + 1) = f(n) + f(n - 1)$；
  • 初始状态： $dp[0] = 0,dp[1] = 1$，即初始化前两个数字；
  • 返回值：$dp[n]$ ，即斐波那契数列的第 n 个数字。

算法分析

  • 时间复杂度O(n)
  • 空间复杂度O(n)

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int fib(int n) {
    // 递归法，时间复杂度太高。
    if(n==0){
        return 0;
    }
    if(n==1){
        return 1;
    }
    // return fib(n-1)+fib(n-2);
    long long a[n+1];
    a[0]=0;
    a[1]=1;
    for(int i=2;i<n+1;i++){
        a[i]=(a[i-1]+a[i-2])%(1000000007);
    }
    return a[n];
}

2 爬楼梯

问题描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？注意：给定 n 是一个正整数。

示例 1：

1
2
3
4
5
输入：2
输出：2
解释： 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

问题分析

策略选择

算法设计

  1. 问题分解划分阶段：规模增长的方向n。线性规模增长。阶段n=1,2,…,n各个阶段。
  2. 确定状态变量：xk，表示k阶段公有xk中爬楼梯的方法
  3. 确定状态转移方程：分为两种情况讨论，如果最后是1步，则x_k =x_k-1。如果最后一步是两步。则x_k=x_k-2。

$$
x_k = x_{k-1}+x_{k-2}
$$
4. 确定边界。x_0=0表示开始的情况。x_k表示当前的结果。x_n表示终止的情况。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public int climbStairs(int n) {
    if (n == 1) {
        return 1;
    }

    int[] dp = new int[n + 1];  // 多开一位，考虑起始位置

    dp[0] = 0; dp[1] = 1; dp[2] = 2;
    for (int i = 3; i <= n; ++i) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }

    return dp[n];
}

3 连续子数组最大和

问题描述

  • 输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为O(n)。

算法设计

  • 状态定义： 设动态规划列表 dp ，dp[i]dp[i] 代表以元素 nums[i]nums[i] 为结尾的连续子数组最大和。
    • 为何定义最大和 dp[i] 中必须包含元素 nums[i] ：保证dp[i] 递推到 dp[i+1]的正确性；如果不包含nums[i] ，递推时则不满足题目的 连续子数组 要求。
  • 转移方程： 若dp[i−1]≤0 ，说明 dp[i - 1]对 dp[i] 产生负贡献，即 dp[i-1] + nums[i]还不如 nums[i]本身大。
    • 当 dp[i - 1] > 0时：执行 dp[i] = dp[i-1] + nums[i]
    • 当 dp[i−1]≤0 时：执行 dp[i] = nums[i]；
  • 初始状态： dp[0] = nums[0]dp[0]=nums[0]，即以 nums[0]nums[0] 结尾的连续子数组最大和为 nums[0]nums[0] 。
  • 返回值： 返回 dp 列表中的最大值，代表全局最大值。

算法分析

  • 时间复杂度 O(N)O(N) ： 线性遍历数组 numsnums 即可获得结果，使用 O(N)O(N) 时间。
  • 空间复杂度 O(1)O(1) ： 使用常数大小的额外空间。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
int maxSubArray(vector<int>& nums) {
    //动态规划有很多不同的方向。例如，这里把动态变化定位不断增加的连续数组的长度。
    // 当连续数组的长度为1,2,3,4,5时，会利用之前计算的结果。求解。但是这很暴力。
    // 相当于求出了当前的所有最长子数组的解。把问题的规模缩小。
    // nums的长度。动态变化。

    // 失败的动态规划，实际上是暴力求解。
    // vector<vector<int>> vec;
    // int max=-999999;
    // vec.push_back(vector<int>());
    // for(int i=0;i<nums.size();i++){
    //     vec[0].push_back(nums[i]);
    //     if(nums[i]>max){
    //         max=nums[i];
    //     }
    // }
    // for(int i=1;i<nums.size();i++){
    //     vec.push_back(vector<int>());
    //     for(int j=0;j<nums.size()-i;j++){
    //         vec[i].push_back(vec[i-1][j]+vec[0][j+i]);
    //         if(vec[i][j]>max){
    //             max=vec[i][j];
    //         }
    //     }
    // }

    // 正常的动态规划
    int max=nums[0];
    vector<int> vec;
    vec.push_back(nums[0]);
    for(int i=1;i<nums.size();i++){
        int temp =nums[i]+vec[i-1];
        if(temp > nums[i]){
            vec.push_back(temp);
        }
        else{
            vec.push_back(nums[i]);
        }
        if(vec[i]>max){
            max=vec[i];
        }
    }
    return max;
}

4 传递信息

问题描述

小朋友 A 在和 ta 的小伙伴们玩传信息游戏，游戏规则如下：

有 n 名玩家，所有玩家编号分别为 0 ～ n-1，其中小朋友 A 的编号为 0
每个玩家都有固定的若干个可传信息的其他玩家（也可能没有）。传信息的关系是单向的（比如 A 可以向 B 传信息，但 B 不能向 A 传信息）。
每轮信息必须需要传递给另一个人，且信息可重复经过同一个人
给定总玩家数 n，以及按 [玩家编号,对应可传递玩家编号] 关系组成的二维数组 relation。返回信息从小 A (编号 0 ) 经过 k 轮传递到编号为 n-1 的小伙伴处的方案数；若不能到达，返回 0。

示例 1：

1
2
3
4
5
输入：n = 5, relation = [[0,2],[2,1],[3,4],[2,3],[1,4],[2,0],[0,4]], k = 3

输出：3

解释：信息从小 A 编号 0 处开始，经 3 轮传递，到达编号 4。共有 3 种方案，分别是 0->2->0->4， 0->2->1->4， 0->2->3->4。

问题分析

策略选择

  • 有三种不同的策略选择：广度优先搜索、深度优先搜索、动态规划。本文采用动态规划的思路，实际上与广度优先搜索的思路是一致的。看在第k步能到达的所有节点。

算法设计

  • 状态定义dp[j] 为经过 i轮传递到编号j 的玩家的方案数，其中k0≤i≤k，n0≤j<n。可以不用记住更久远的历史状态。
  • 转移方程
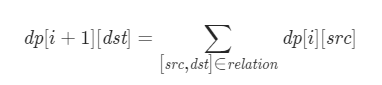
  • 初始状态 dp[0]=1
  • 终止状态 最终得到dp[n−1] 即为总的方案数

算法分析

  • 时间复杂度：O(km)。其中 m 为 relation 数组的长度。
  • 空间复杂度：O(n)O(n)。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class Solution {
public:
    int numWays(int n, vector<vector<int>>& relation, int k) {
        // // 构建邻接矩阵
        // vector<vector<int>> vec(n,vector<int>(n,0));
        // for(auto a:relation){
        //     vec[a[0]][a[1]]=1;
            
        // }
        // // for(int i=0;i<n;i++){
        // //     for(int j=0;j<n;j++){
        // //         cout<<vec[i][j]<<"\t";
        // //     }
        // //     cout<<endl;
        // // }
        // // 构建有向图


        // vector<int> result;
        // result.push_back(0);
        // for(int i=0;i<k;i++){
        //     // for(int k:result){
        //     //     cout<<k<<"\t";
        //     // }
        //     // cout<<endl;
        //     vector<int> temp;
        //     for(auto a:result){
        //         for(int j=0;j<n;j++){
        //             if(vec[a][j]==1)temp.push_back(j);
        //         }
        //     }
        //     result.assign(temp.begin(),temp.end());

        // }
        // int sum =0;
        // for(auto a:result){
        //     if(a==n-1)sum++;
        // }
        // return sum;

        // 尝试使用动态规划求解。可以不用构建关系矩阵，每次遍历关系矩阵就好了。。然后每轮迭代能够到的位置。
        vector<int> dp(n,0);
        dp[0]=1;
        for(int i=0;i<k;i++){
            vector<int> temp(n,0);
            for(auto a: relation){
                temp[a[1]]+=dp[a[0]];
            }
            dp.assign(temp.begin(),temp.end());
        }
        return dp[n-1];

    }
};