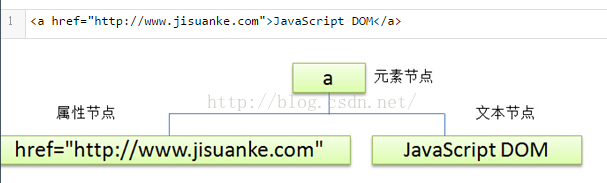
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| bool exist(vector<vector<char>>& board, string word) {
for(int i=0;i<board.size();i++){
for(int j=0;j<board[0].size();j++){
if(dfs(board,word,i,j,0)==true){
return true;
}
}
}
return false;
}
bool dfs(vector<vector<char>> & board,string &word,int row,int col,int k){
if(row<0 || col <0 ||row>=board.size()||col>=board[0].size())return false;
// cout<<word[k]<<" "<<board[row][col]<<endl;
if(word[k]!=board[row][col])return false;
if(k==word.size()-1)return true;
// cout<<row<<" "<<col<<endl;
char temp = board[row][col];
board[row][col]='\0';
bool result = dfs(board,word,row+1,col,k+1)
|| dfs(board,word,row-1,col,k+1)
|| dfs(board,word,row,col-1,k+1)
|| dfs(board,word,row,col+1,k+1);
board[row][col]=temp;
return result;
}
|