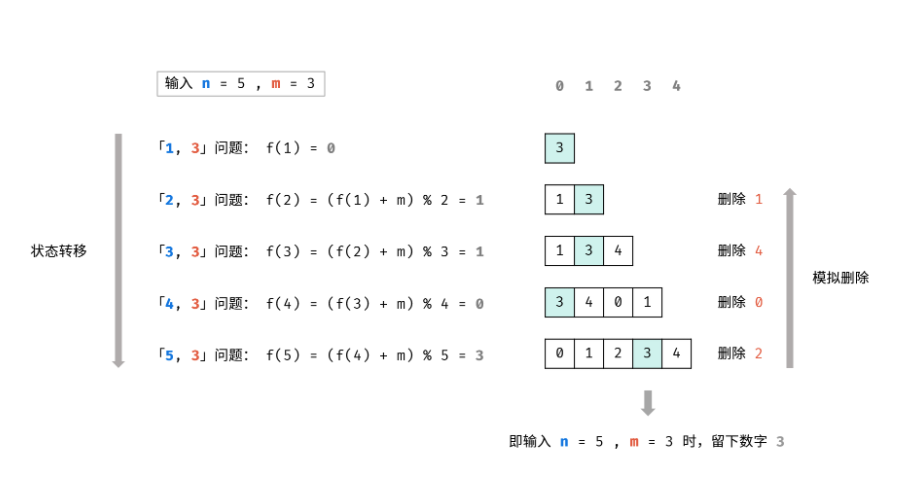
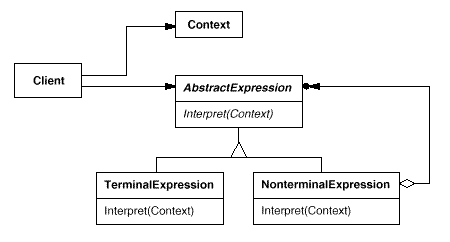
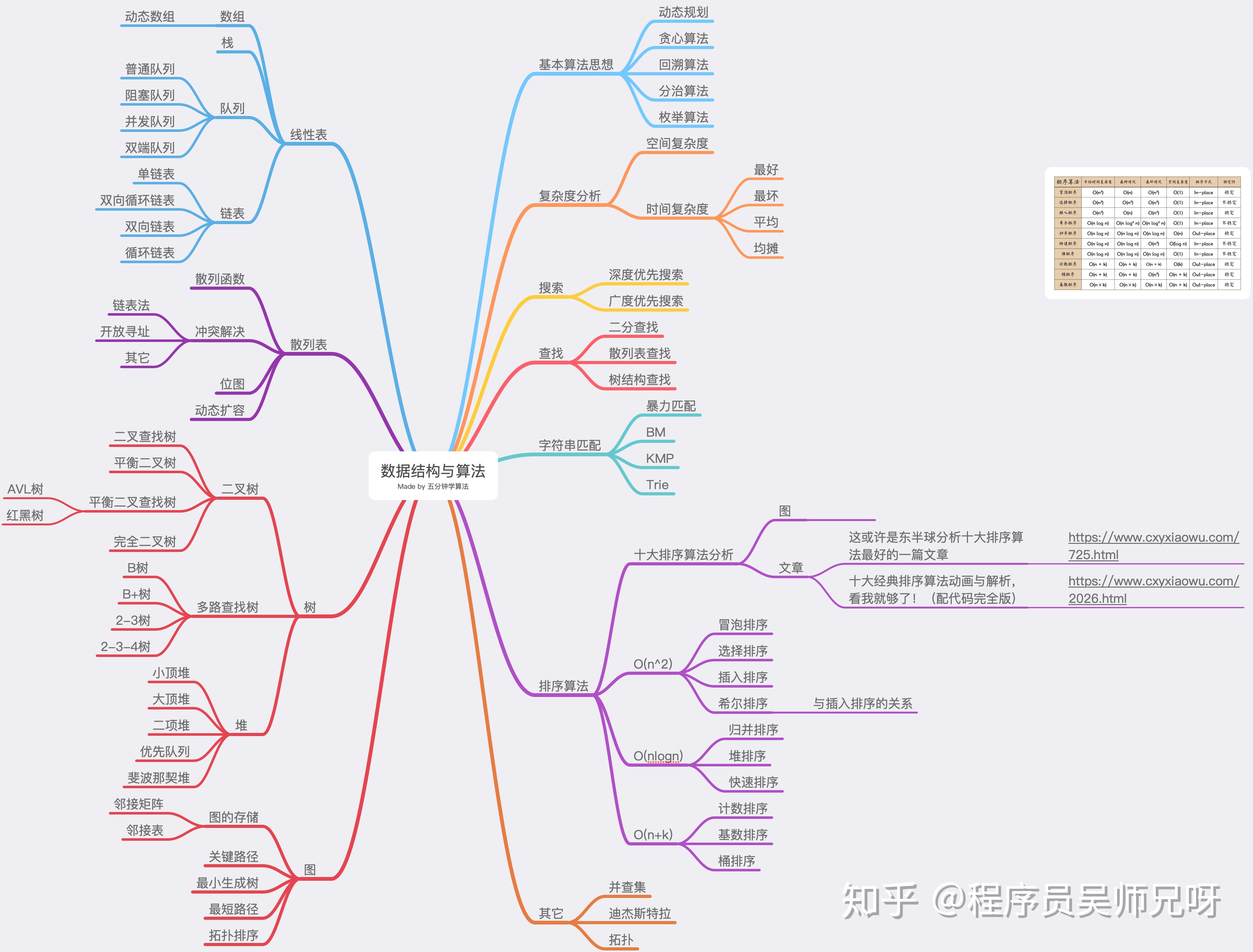
2.1 深搜与广搜
树的遍历
1 树的子结构
- 输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构).B是A的子结构, 即 A中有出现和B相同的结构和节点值。
- 链接
2 树的镜像
- 请完成一个函数,输入一个二叉树,该函数输出它的镜像。
- 链接
3 对称的二叉树
- 请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
- 链接
4 二叉搜索树的第k大节点
- 给定一棵二叉搜索树,请找出其中第k大的节点。
- 示例 1:
1 | 输入: root = [3,1,4,null,2], k = 1 |
5 二叉树的深度
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。
例如:
1 | 给定二叉树 [3,9,20,null,null,15,7], |
6 平衡二叉树
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
示例 1:
1 | 给定二叉树 [3,9,20,null,null,15,7] |
7 二叉搜索树的最近公共祖先
问题描述
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树:
1 | root = [6,2,8,0,4,7,9,null,null,3,5] |
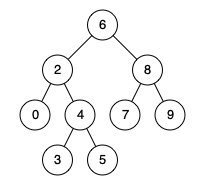
- 示例 1:
1 | 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 |
问题分析
策略选择
算法设计
算法分析
算法实现
1 | /** |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Estom的博客!