1 二叉树与双向链表

问题分析

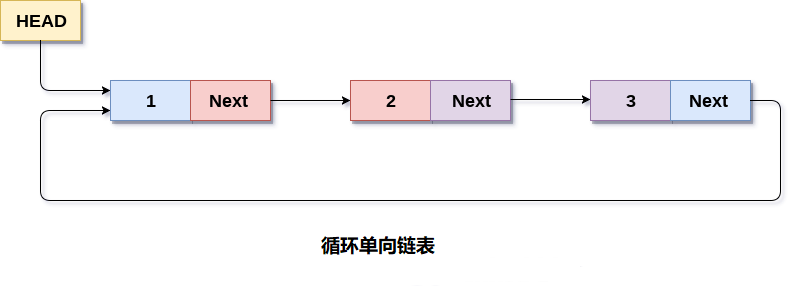
  • 输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。
  • 链接

1.1 二叉树与双向链表——左旋右旋

借鉴了构建二叉平衡树的内容。可以自己完成以下二叉平衡树试试。

算法设计

  • 通过左旋右旋操作实现树的旋转。最终旋转成一个倒V树。

算法分析

  • 时间复杂度O(n)
  • 空间复杂度O(n)

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
class Solution {
public:
    Node* treeToDoublyList(Node* root) {
        // 类似于二叉平衡树的左旋右旋。
        if(root==nullptr){
            return nullptr;
        }
        // 进行左旋和右旋
        m[root]=nullptr;
        m[root->left]=root;
        m[root->right]=root;
        rotate_left(root->left);
        rotate_right(root->right);

        // 旋转完成后，制作循环链表
        Node* temp_left=root;
        while(temp_left->left!=nullptr){
            temp_left=temp_left->left;
        }

        Node* temp_right=root;
        while(temp_right->right!=nullptr){
            temp_right=temp_right->right;
        }
        temp_right->right=temp_left;
        temp_left->left = temp_right;
        // 返回链表的最左端
        return temp_left;
    }
    //使用map来记录父节点
    map<Node*,Node*> m;
    //左树有右节点，则左旋
    void rotate_left(Node* root){
        if(root==nullptr){
            return;
        }
        // 头递归，子树完成了旋转再旋转本树
        m[root->left]=root;
        m[root->right]=root;
        rotate_left(root->left);
        rotate_right(root->right);
        // 右树为空，不需要左旋,只需要改变一个连接，right指向父节点
        if(root->right==nullptr){
            root->right=m[root];
            return;
        }
        // 右树不为空。则找到右子树。插入到本节点和父节点之间
        Node* temp_right=root->right;
        while(temp_right->right!=nullptr){
            temp_right=temp_right->right;
        }
        // 改变3个连接。最后一个右节点与父节点相互指向。右节点的做节点指向这一个。
        temp_right->right=m[root];
        m[root]->left=temp_right;
        root->right->left=root;
        return ;
    }
    // 右树有左节点，则右旋
    void rotate_right(Node* root){
        if(root==nullptr){
            return;
        }
        // 头递归，子树完成了旋转再旋转本树
        m[root->left]=root;
        m[root->right]=root;
        rotate_left(root->left);
        rotate_right(root->right);

        // 左树为空，不需要旋转
        if(root->left==nullptr){
            root->left=m[root];
            return;
        }
        // 左树不为空
        Node* temp_left=root->left;
        while(temp_left->left!=nullptr){
            temp_left=temp_left->left;
        }
        // 对称
        temp_left->left=m[root];
        m[root]->right=temp_left;
        root->left->right=root;
        return ;
    }

1.2 二叉树与双向链表——中序遍历输出

算法设计

  • 按中序遍历输出链表。
  • 那么就用中序遍历的前一个节点指向本节点。

算法分析

  • 时间复杂度O(n)
  • 空间复杂度O(1)

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public:
    Node* treeToDoublyList(Node* root) {
        if(root == nullptr) return nullptr;
        dfs(root);
        head->left = pre;
        pre->right = head;
        return head;
    }
private:
    Node *pre, *head;
    void dfs(Node* cur) {
        if(cur == nullptr) return;
        dfs(cur->left);
        if(pre != nullptr) pre->right = cur;
        else head = cur;
        cur->left = pre;
        pre = cur;
        dfs(cur->right);
    }

2 堆树的上浮下沉操作

3 二叉平衡树的左旋右旋