数组与滑动窗口

1 最长不含重复字符的子字符串——滑动窗口

问题描述

  • 请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。

问题分析

问题分类

算法设计

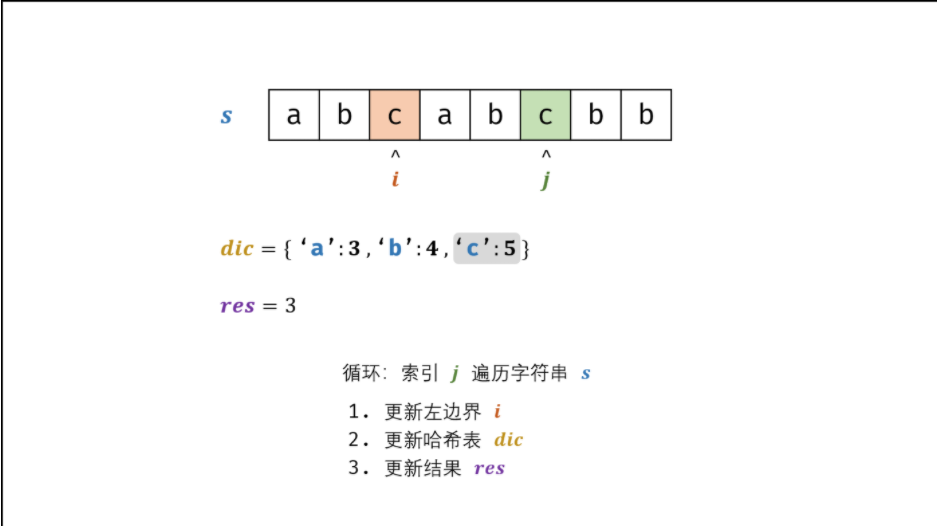
  • 哈希表 dicdic 统计： 指针 jj 遍历字符 ss ，哈希表统计字符 s[j]s[j] 最后一次出现的索引 。
  • 更新左指针 ii ： 根据上轮左指针 ii 和 dic[s[j]]dic[s[j]] ，每轮更新左边界 ii ，保证区间 [i + 1, j][i+1,j] 内无重复字符且最大。
    $$
    i=max(dic[s[j]],i)
    $$
  • 更新结果 res ： 取上轮 res 和本轮双指针区间 [i + 1,j][i+1,j] 的宽度（即 j - ij−i ）中的最大值

$$
res=max(res,j−i)
$$

算法分析

  • 时间复杂度 O(N)： 其中 N为字符串长度，动态规划需遍历计算 dpdp 列表。
  • 空间复杂度 O(1) ： 字符的 ASCII 码范围为 00 ~ 127，哈希表 dic最多使用 O(128) = O(1) 大小的额外空间。

算法分析

  • 时间复杂度 O(N)O(N) ： 其中 NN 为字符串长度，动态规划需遍历计算 dpdp 列表。
  • 空间复杂度 O(1)O(1) ： 字符的 ASCII 码范围为 00 ~ 127127 ，哈希表 dicdic 最多使用 O(128) = O(1)O(128)=O(1) 大小的额外空间。

算法实现

1
2
3
4
5
6
7
8
9
10
11
int lengthOfLongestSubstring(string s) {
    vector<int> a(200,-1);
    int repeat=-1;
    int max_val=0;
    for(int i=0;i<s.size();i++){
        repeat=max(a[s[i]],repeat);
        max_val=max(i-repeat,max_val);
        a[s[i]]=i;
    }
    return max_val;
}

2 盛最多水的容器

问题描述

给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器。

1
2
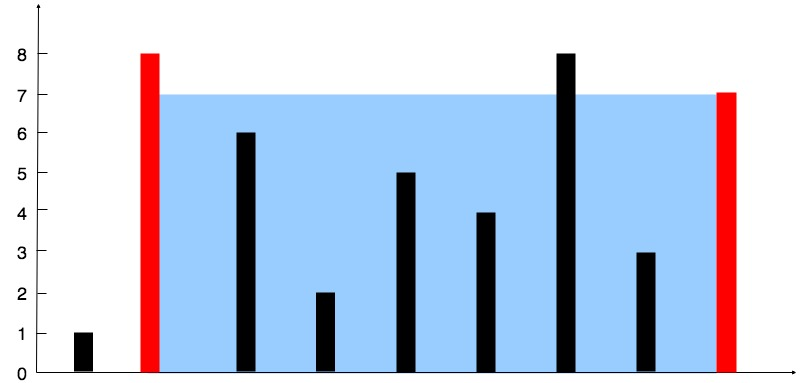
3
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

问题分析

策略选择

  • 双指针。本质上是一种反向贪心思想。虽然我不知道做出选择是不是最好。但是我每次一定都能把更坏的情况舍弃掉。
  • 与二维有序矩阵查找的题非常类似。都是舍弃掉坏的情况，进行线性贪心。

算法设计

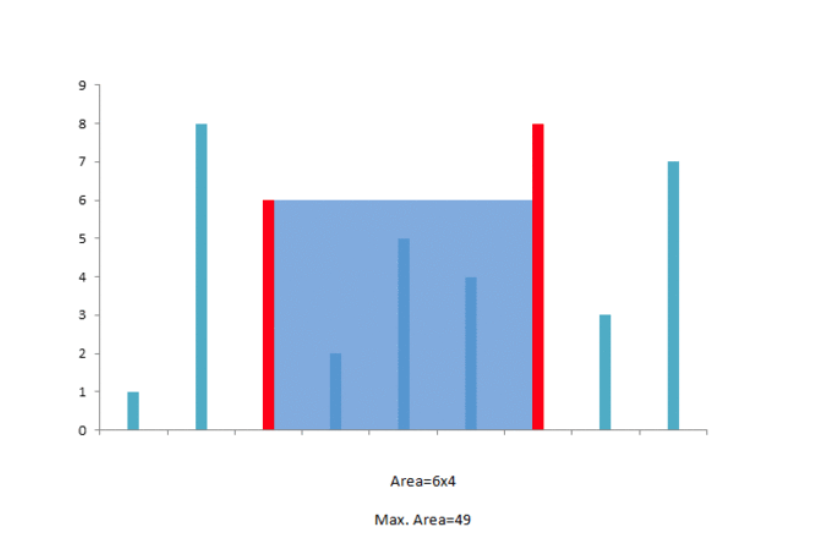
  • 双指针贪心思想：对应数字较小的那个指针以后不可能作为容器的边界了，将其丢弃，并移动对应的指针。
  • 计算公式：两个指针指向的数字中较小值∗指针之间的距离

算法分析

  • 时间复杂度O(n)
  • 空间复杂度O(1)

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int maxArea(vector<int>& height) {
    int i=0,j=height.size()-1;
    int max_val=0;
    while(i<j){
        max_val=max(max_val,(j-i)*min(height[i],height[j]));
        if(height[i]<height[j]){
            i++;
        }
        else{
            j--;
        }
    }
    return max_val;
}