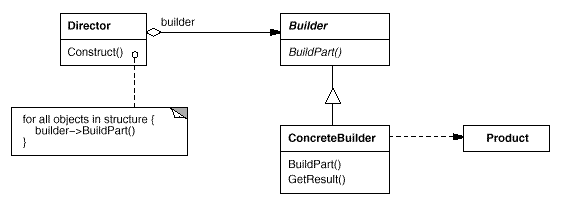
4.2 表示数值的字符串
表示数值的字符串
1 表示数值的字符串
问题描述
- 请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串”+100”、”5e2”、”-123”、”3.1416”、”-1E-16”、”0123”都表示数值,但”12e”、”1a3.14”、”1.2.3”、”+-5”及”12e+5.4”都不是。
- 链接
问题分析
这题一看,明显就是有限状态自动机。词法分析过程中用来判断关键字、数值的。属于暴力破解。使用优先状态自动机。确定分类讨论的情况。找到符合规则的所有的路。
另外提供了另外一种暴力破解的思路。通过讨论违反规则的情况。找到违反规则的所有的路。
提供了两种截然不同的分类讨论的思路。在某些情况下,第二种思路反而会简单很多。
在 C++ 文档 中,描述了一个合法的数值字符串应当具有的格式。具体而言,它包含以下部分:
- 符号位,即 +、− 两种符号
- 整数部分,即由若干字符 0-9组成的字符串
- 小数点
- 小数部分,其构成与整数部分相同
- 指数部分,其中包含开头的字符 e(大写小写均可)、可选的符号位,和整数部分
问题分类
- 枚举法
- 正向分类讨论和反向分类讨论
1.1 表示数值的字符串——有限状态自动机DFA
选择策略
- 有限状态自动机
- 正向分类讨论
算法设计
字符类型:空格 「 」、数字「 0—9 」 、正负号 「 +− 」 、小数点 「 .」 、幂符号 「 eE 」
状态定义:按照字符串从左到右的顺序,定义以下 9 种状态。
- 开始的空格
- 幂符号前的正负号
- 小数点前的数字
- 小数点、小数点后的数字
- 当小数点前为空格时,小数点、小数点后的数字
- 幂符号
- 幂符号后的正负号
- 幂符号后的数字
- 结尾的空格
状态转移图
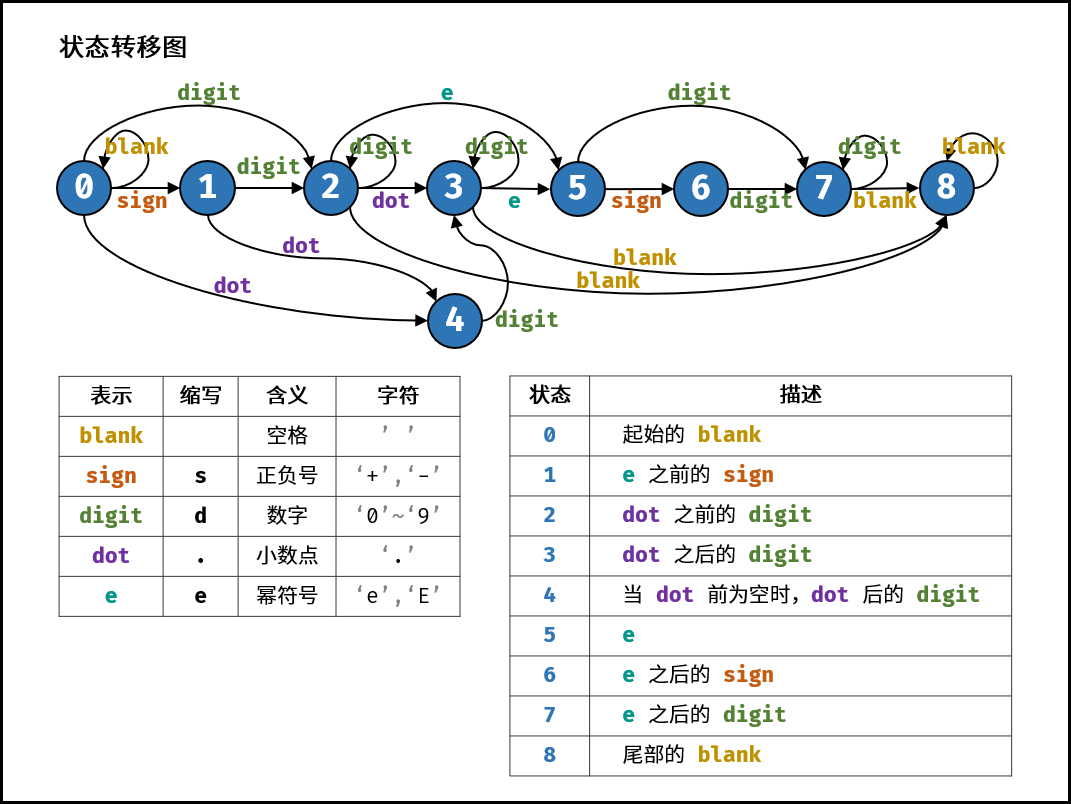
算法分析
- 时间复杂度O(n)
- 空间复杂度O(n)
算法实现
1 | // 方法一:有限状态自动机DFA,时间复杂度 O(N) |
1.2 表示数值的字符串——反向分类讨论
算法设计
讨论所有可能出现的反例
e/E 分割为指数和底数
- 底数:
- 只能有一个+-号位于第一位
- 只能有一个小数点
- 指数
- 只能有一个+-号位于第一位
- 不能有小数点
- 底数:
算法分析
- 时间复杂度O(n)
- 空间复杂度O()
算法实现
1 | class Solution { |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Estom的博客!