1 队列的最大值

问题描述

  • 请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。

  • 若队列为空，pop_front 和 max_value 需要返回 -1

  • 示例 1：

1
2
3
4
输入: 
["MaxQueue","push_back","push_back","max_value","pop_front","max_value"]
[[],[1],[2],[],[],[]]
输出: [null,null,null,2,1,2]

问题分析

策略选择

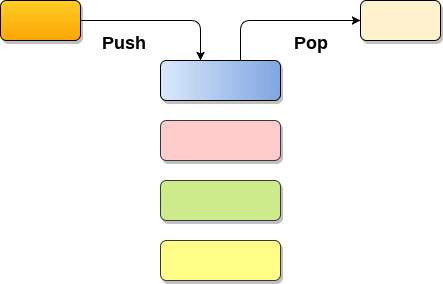
  • 数据结构：单调队列
  • 算法思想：后入的较大值，会把之前的较大值排除。但是后入的次大值，不会将之前的最大值排出队列。所以维护两个队列，一个用来删除元素，一个用来找到最大值（单调队列）

算法设计

  • 本算法基于问题的一个重要性质：当一个元素进入队列的时候，它前面所有比它小的元素就不会再对答案产生影响。

  • 举个例子，如果我们向队列中插入数字序列 1 1 1 1 2，那么在第一个数字 2 被插入后，数字 2 前面的所有数字 1 将不会对结果产生影响。因为按照队列的取出顺序，数字 2 只能在所有的数字 1 被取出之后才能被取出，因此如果数字 1 如果在队列中，那么数字 2 必然也在队列中，使得数字 1 对结果没有影响。

  • 按照上面的思路，我们可以设计这样的方法：从队列尾部插入元素时，我们可以提前取出队列中所有比这个元素小的元素，使得队列中只保留对结果有影响的数字。这样的方法等价于要求维持队列单调递减，即要保证每个元素的前面都没有比它小的元素。

  • 那么如何高效实现一个始终递减的队列呢？我们只需要在插入每一个元素 value 时，从队列尾部依次取出比当前元素 value 小的元素，直到遇到一个比当前元素大的元素 value’ 即可。

  • 上面的过程保证了只要在元素 value 被插入之前队列递减，那么在 value 被插入之后队列依然递减。
    而队列的初始状态（空队列）符合单调递减的定义。
    由数学归纳法可知队列将会始终保持单调递减。

算法分析

  • 时间复杂度O(1)
  • 空间复杂度O(n)

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class MaxQueue {
    queue<int> q;
    deque<int> d;
public:
    MaxQueue() {
    }
    
    int max_value() {
        if (d.empty())
            return -1;
        return d.front();
    }
    
    void push_back(int value) {
        while (!d.empty() && d.back() < value) {
            d.pop_back();
        }
        d.push_back(value);
        q.push(value);
    }
    
    int pop_front() {
        if (q.empty())
            return -1;
        int ans = q.front();
        if (ans == d.front()) {
            d.pop_front();
        }
        q.pop();
        return ans;
    }
};