一、PyTorch 60分钟

1 概述

什么是 PyTorch？

PyTorch 是基于以下两个目的而打造的python科学计算框架：

  • 无缝替换NumPy，并且通过利用GPU的算力来实现神经网络的加速。
  • 通过自动微分机制，来让神经网络的实现变得更加容易。

本次教程的目标：

  • 深入了解PyTorch的张量单元以及如何使用Pytorch来搭建神经网络。
  • 自己动手训练一个小型神经网络来实现图像的分类。

2 模块

当前需要了解的模块

  1. torch
  2. torch.Tensor
  3. torch.nn.*
  4. torch.nn.Function
  5. torch.optim
  6. torch.util.data
  7. torch.util.tensorboard

2.1 torch模块

1
2
3
4
5
6
import torch
torch.randn()
torch.from_numpy()
torch.linspace()
torch.ones()
torch.eye()

包含了多维张量的数据结构以及基于其上的多种数学操作。另外，它也提供了多种工具，其中一些可以更有效地对张量和任意类型进行序列化。具体包括pytorch张量的生成，以及运算、切片、连接等操作，还包括神经网络中经常使用的激活函数，比如sigmoid、relu、tanh，还提供了与numpy的交互操作

  • 该模块定义了大量对tensor操作的方法，能够返回tensor

2.2 torch.Tensor模块类

1
2
3
4
5
6
import torch
a = torch.tensor()

# 返回操作和自操作
a.exp()
a.exp_()

numpy作为Python中数据分析的专业第三方库，比Python自带的Math库速度更快。同样的，在PyTorch中，有一个类似于numpy的库，称为Tensor。Tensor可谓是神经网络界的numpy

  • 定义了tensor对象的一系列操作。自己的操作。

2.3 torch.sparse

在做nlp任务时，有个特点就是特征矩阵是稀疏矩阵。torch.sparse模块定义了稀疏张量，采用的是COO格式，主要方法是用一个长整型定义非零元素的位置，用浮点数张量定义对应非零元素的值。稀疏张量之间可以做加减乘除和矩阵乘法。从而有效地存储和处理大多数元素为零的张量。

2.4 torch.cuda

该模块定义了与cuda运算的一系列函数，比如检查系统的cuda是否可用，在多GPU情况下，查看显示当前进程对应的GPU序号，清除GPU上的缓存，设置GPU的计算流，同步GPU上执行的所有核函数等。

2.5 torch.nn.*模块

torch.nn是pytorch神经网络模块化的核心，这个模块下面有很多子模块，包括卷积层nn.ConvNd和线性层（全连接层）nn.Linear等。当构建深度学习模型的时候，可以通过继承nn.Module类并重写forward方法来实现一个新的神经网络。另外，torch.nn中也定义了一系列的损失函数，包括平方损失函数torch.nn.MSELoss、交叉熵损失函数torch.nn.CrossEntropyLoss等。

  • 定义了一系列对象化的算子层。包含各种tensor表示的参数。包含一系列子模块。对象化后，一个算子表示一层的输入输出和操作。而函数化的时候，指标是单个路径上的输入输出操作。
    • nn.Module 表示神经网络对象。包含forward()/parameters()/modules()/zero_grad()
    • nn.Sequential处理序列化的module
    • nn.Conv1d/nn.Conv2d/nn.Conv3d卷积层模块
    • nn.MaxPool1d/nn.MaxPool2d/nn.MaxPool3d最大池化层模块
    • nn.AvgPool1d/nn.AvgPool2d/nn.AvgPool3d平均池化层
    • nn.ReLU/nn.ELU/nn.Sigmod/nn.Tanh/nn.LogSigmod线性全连接层
    • nn.Softmin/nn.Softmax/nn.Softshrink/nn.Softsign/nn.Softplus全连接层
    • nn.BatchNomal1d/nn.BatchNoraml2d/nn.BatchNoraml3d归一化层
    • nn.RNN循环神经元层
    • nn.Function函数化的各种算子。参考下一个

2.6 torch.nn.Functional函数模块

该模块定义了一些与神经网络相关的函数，包括卷积函数和池化函数等，torch.nn中定义的模块一般会调用torch.nn.functional里的函数，比如，nn.ConvNd会调用torch.nn.functional.convNd函数。另外，torch.nn.functional里面还定义了一些不常用的激活函数，包括torch.nn.functional.relu6和torch.nn.functional.elu等。

  • 定义了一系列函数化的算子。包含各种tensor表示的参数。可以把它看做nn的一个子模块。而且提供更加精细快速的神经网络构建过程

2.7 torch.nn.init模块

该模块定义了神经网络权重的初始化，包括均匀初始化torch.nn.init.uniform_和正太分布归一化torch.nn.init.normal_等。值得注意得是，在pytorch中函数或者方法如果以下划线结尾，则这个方法会直接改变作用张量的值，因此，这些方法会直接改变传入张量的值，同时会返回改变后的张量。

2.8 torch.optim模块

torch.optim模块定义了一系列的优化器，比如torch.optim.SGD、torch.optim.AdaGrad、torch.optim.RMSProp、torch.optim.Adam等。还包含学习率衰减的算法的模块torch.optim.lr_scheduler，这个模块包含了学习率阶梯下降算法torch.optim.lr_scheduler.StepLR和余弦退火算法torch.optim.lr_scheduler.CosineAnnealingLR

  • torch.optim.SGD、
  • torch.optim.AdaGrad、
  • torch.optim.RMSProp、
  • torch.optim.Adam

2.9 torch.autograd模块

该模块是pytorch的自动微分算法模块，定义了一系列自动微分函数，包括torch.autograd.backward函数，主要用于在求得损失函数后进行反向梯度传播。torch.autograd.grad函数用于一个标量张量（即只有一个分量的张量）对另一个张量求导，以及在代码中设置不参与求导的部分。另外，这个模块还内置了数值梯度功能和检查自动微分引擎是否输出正确结果的功能。

2.10 torch.distributed模块

torch.distributed是pytorch的分布式计算模块，主要功能是提供pytorch的并行运行环境，其主要支持的后端有MPI、Gloo和NCCL三种。pytorch的分布式工作原理主要是启动多个并行的进程，每个进程都拥有一个模型的备份，然后输入不同的训练数据到多个并行的进程，计算损失函数，每个进行独立地做反向传播，最后对所有进程权重张量的梯度做归约（Redue）。用到后端的部分主要是数据的广播（Broadcast）和数据的收集（Gather），其中，前者是把数据从一个节点（进程）传播到另一个节点（进程），比如归约后梯度张量的传播，后者则把数据从其它节点转移到当前节点，比如把梯度张量从其它节点转移到某个特定的节点，然后对所有的张量求平均。pytorch的分布式计算模块不但提供了后端的一个包装，还提供了一些启动方式来启动多个进程，包括但不限于通过网络（TCP）、环境变量、共享文件等。

2.11 torch.distributions模块

该模块提供了一系列类，使得pytorch能够对不同的分布进行采样，并且生成概率采样过程的计算图。在一些应用过程中，比如强化学习，经常会使用一个深度学习模型来模拟在不同环境条件下采取的策略，其最后的输出是不同动作的概率。当深度学习模型输出概率之后，需要根据概率对策略进行采样来模拟当前的策略概率分布，最后用梯度下降方法来让最优策略的概率最大（这个算法称为策略梯度算法，Policy Gradient）。实际上，因为采样的输出结果是离散的，无法直接求导，所以不能使用反keh.distributions.Categorical类，pytorch还支持其它分布。比如torch.distributions.Normal类支持连续的正太分布的采样，可以用于连续的强化学习的策略。

2.12 torch.hub模块

该模块提供了一系列预训练的模型供用户使用。比如，可以通过torch.hub.list函数来获取某个模型镜像站点的模型信息。通过torch.hub.load来载入预训练的模型，载入后的模型可以保存到本地，并可以看到这些模型对应类支持的方法。

2.13 torch.jit模块

该模块是pytorch的即时编译器模块。这个模块存在的意义是把pytorch的动态图转换成可以优化和序列化的静态图，其主要工作原理是通过预先定义好的张量，追踪整个动态图的构建过程，得到最终构建出来的动态图，然后转换为静态图。通过JIT得到的静态图可以被保存，并且被pytorch其它前端（如C++语言的前端）支持。另外，JIT也可以用来生成其它格式的神经网络描述文件，如ONNX。torch.jit支持两种模式，即脚本模式（ScriptModule）和追踪模式（Tracing）。两者都能构建静态图，区别在于前者支持控制流，后者不支持，但是前者支持的神经网络模块比后者少。

2.14 torch.multiprocessing模块

该模块定义了pytorch中的多进程API，可以启动不同的进程，每个进程运行不同的深度学习模型，并且能够在进程间共享张量。共享的张量可以在CPU上，也可以在GPU上，多进程API还提供了与python原生的多进程API（即multiprocessing库）相同的一系列函数，包括锁（Lock）和队列（Queue）等。

2.15 torch.random模块

该模块提供了一系列的方法来保存和设置随机数生成器的状态，包括使用get_rng_state函数获取当前随机数生成器的状态，set_rng_state函数设置当前随机数生成器状态，并且可以使用manual_seed函数来设置随机种子，也可以使用initial_seed函数来得到程序初始的随机种子。因为神经网络的训练是一个随机的过程，包括数据的输入、权重的初始化都具有一定的随机性。设置一个统一的随机种子可以有效地帮助我们测试不同神经网络地表现，有助于调试神经网络地结构。

2.16 torch.onnx模块

该模块定义了pytorch导出和载入ONNX格式地深度学习模型描述文件。ONNX格式地存在是为了方便不同深度学习框架之间交换模型。引入这个模块可以方便pytorch导出模型给其它深度学习框架使用，或者让pytorch载入其它深度学习框架构建地深度学习模型。

2.17 torch.utils模块

该模块提供了一系列地工具来帮助神经网络地训练、测试和结构优化。这个模块主要包含以下6个子模块：

1 torch.utils.bottleneck模块

该模块可以用来检查深度学习模型中模块地运行时间，从而可以找到性能瓶颈的那些模块，通过优化那些模块的运行时间，从而优化整个深度学习的模型的性能。

2 torch.utils.checkpoint模块

该模块可以用来节约深度学习使用的内存。通过前面的介绍我们知道，因为要进行梯度反向传播，在构建计算图的时候需要保存中间的数据，而这些数据大大增加了深度学习的内存消耗。为了减少内存消耗，让迷你批次的大小得到提高，从而提升深度学习模型的性能和优化时的稳定性，我们可以通过这个模块记录中间数据的计算过程，然后丢弃这些中间数据，等需要用到的时候再重新计算这些数据。这个模块设计的核心思想是以计算时间换内存空间，如果使用得当，深度学习模型的性能可以有很大的提升。

3 torch.utils.cpp_extension模块

该模块定义了pytorch的C++扩展，其主要包含两个类：CppExtension定义了使用C++来编写的扩展模块的源代码相关信息，CUDAExtension则定义了C++/CUDA编写的扩展模块的源代码相关信息。再某些情况下，用户可能使用C++实现某些张量运算和神经网络结构（比如pytorch没有类似功能的模块或者类似功能的模块性能比较低），该模块就提供了一个方法能够让python来调用C++/CUDA编写的深度学习扩展模块。在底层上，这个扩展模块使用了pybind11,保持了接口的轻量性并使得pytorch易于被扩展。

4 torch.utils.data模块

该模块引入了 数据集（Dataset）和数据载入器（DataLoader） 的概念，前者代表包含了所有数据的数据集，通过索引能够得到某一条特定的数据，后者通过对数据集的包装，可以对数据集进行 随机排列（Shuffle）和采样（Sample） ,得到一系列打乱数据的迷你批次。

5 torch.util.dlpacl模块

该模块定义了pytorch张量和DLPackz张量存储格式之间的转换，用于不同框架之间张量数据的交换。

6 torch.utils.tensorboard模块

该模块是pytorch对TensorBoard数据可视化工具的支持。TensorBoard原来是TensorFlow自带的数据可视化工具，能够显示深度学习模型在训练过程中损失函数、张量权重的直方图，以及模型训练过程中输出的文本、图像和视频等。TensorBoard的功能非常强大，而且是基于可交互的动态网页设计的，使用者可以通过预先提供的一系列功能来输出特定的训练过程的细节（如某一神经网络层的权重的直方图，以及训练过程中某一段时间的损失函数等）pytorch支持TensorBoard可视化后，在训练过程中，可以很方便地观察中间输出地张量，也可以方便地调试深度学习模型。

二、张量

张量如同数组和矩阵一样, 是一种特殊的数据结构。在PyTorch中, 神经网络的输入、输出以及网络的参数等数据, 都是使用张量来进行描述。

张量的使用和Numpy中的ndarrays很类似, 区别在于张量可以在GPU或其它专用硬件上运行, 这样可以得到更快的加速效果。如果你对ndarrays很熟悉的话, 张量的使用对你来说就很容易了。如果不太熟悉的话, 希望这篇有关张量API的快速入门教程能够帮到你。

1
2
import torch
import numpy as np

1 张量初始化

张量有很多种不同的初始化方法, 先来看看四个简单的例子：

2. 直接生成张量

由原始数据直接生成张量, 张量类型由原始数据类型决定。

1
2
data = [[1, 2], [3, 4]]
x_data = torch.tensor(data)

2. 通过Numpy数组来生成张量

由已有的Numpy数组来生成张量(反过来也可以由张量来生成Numpy数组, 参考张量与Numpy之间的转换)。

1
2
np_array = np.array(data)
x_np = torch.from_numpy(np_array)

3. 通过已有的张量来生成新的张量

新的张量将继承已有张量的数据属性(结构、类型), 也可以重新指定新的数据类型。

1
2
3
4
5
6
7
8
x_ones = torch.ones_like(x_data)   # 保留 x_data 的属性
print(f"Ones Tensor: \n {x_ones} \n")

x_rand = torch.rand_like(x_data, dtype=torch.float)   # 重写 x_data 的数据类型

int -> float

print(f"Random Tensor: \n {x_rand} \n")

显示:

1
2
3
4
5
6
7
Ones Tensor:
 tensor([[1, 1],
         [1, 1]])

Random Tensor:
 tensor([[0.0381, 0.5780],
         [0.3963, 0.0840]])

4. 通过指定数据维度来生成张量

shape是元组类型, 用来描述张量的维数, 下面3个函数通过传入shape来指定生成张量的维数。

1
2
3
4
5
6
7
8
shape = (2,3,)
rand_tensor = torch.rand(shape)
ones_tensor = torch.ones(shape)
zeros_tensor = torch.zeros(shape)

print(f"Random Tensor: \n {rand_tensor} \n")
print(f"Ones Tensor: \n {ones_tensor} \n")
print(f"Zeros Tensor: \n {zeros_tensor}")

显示:

1
2
3
4
5
6
7
8
9
10
11
Random Tensor:
 tensor([[0.0266, 0.0553, 0.9843],
         [0.0398, 0.8964, 0.3457]])

Ones Tensor:
 tensor([[1., 1., 1.],
         [1., 1., 1.]])

Zeros Tensor:
 tensor([[0., 0., 0.],
         [0., 0., 0.]])

2 张量属性

从张量属性我们可以得到张量的维数、数据类型以及它们所存储的设备(CPU或GPU)。

来看一个简单的例子:

1
2
3
4
5
tensor = torch.rand(3,4)

print(f"Shape of tensor: {tensor.shape}")
print(f"Datatype of tensor: {tensor.dtype}")
print(f"Device tensor is stored on: {tensor.device}")

显示:

1
2
3
Shape of tensor: torch.Size([3, 4])   # 维数
Datatype of tensor: torch.float32     # 数据类型
Device tensor is stored on: cpu       # 存储设备

3 张量运算

有超过100种张量相关的运算操作, 例如转置、索引、切片、数学运算、线性代数、随机采样等。更多的运算可以在这里查看。

所有这些运算都可以在GPU上运行(相对于CPU来说可以达到更高的运算速度)。如果你使用的是Google的Colab环境, 可以通过 Edit > Notebook Settings 来分配一个GPU使用。

1
2
3
# 判断当前环境GPU是否可用, 然后将tensor导入GPU内运行
if torch.cuda.is_available():
  tensor = tensor.to('cuda')

光说不练假把式, 接下来的例子一定要动手跑一跑。如果你对Numpy的运算非常熟悉的话, 那tensor的运算对你来说就是小菜一碟。

1. 张量的索引和切片

1
2
3
tensor = torch.ones(4, 4)
tensor[:,1] = 0            # 将第1列(从0开始)的数据全部赋值为0
print(tensor)

显示:

1
2
3
4
tensor([[1., 0., 1., 1.],
        [1., 0., 1., 1.],
        [1., 0., 1., 1.],
        [1., 0., 1., 1.]])

2. 张量的拼接

你可以通过torch.cat方法将一组张量按照指定的维度进行拼接, 也可以参考torch.stack方法。这个方法也可以实现拼接操作, 但和torch.cat稍微有点不同。

1
2
t1 = torch.cat([tensor, tensor, tensor], dim=1)
print(t1)

显示:

1
2
3
4
tensor([[1., 0., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1.],
        [1., 0., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1.],
        [1., 0., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1.],
        [1., 0., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1.]])

3. 张量的乘积和矩阵乘法

1
2
3
4
# 逐个元素相乘结果
print(f"tensor.mul(tensor): \n {tensor.mul(tensor)} \n")
# 等价写法:
print(f"tensor * tensor: \n {tensor * tensor}")

显示:

1
2
3
4
5
6
7
8
9
10
11
tensor.mul(tensor):
 tensor([[1., 0., 1., 1.],
        [1., 0., 1., 1.],
        [1., 0., 1., 1.],
        [1., 0., 1., 1.]])

tensor * tensor:
 tensor([[1., 0., 1., 1.],
        [1., 0., 1., 1.],
        [1., 0., 1., 1.],
        [1., 0., 1., 1.]])

下面写法表示张量与张量的矩阵乘法:

1
2
3
print(f"tensor.matmul(tensor.T): \n {tensor.matmul(tensor.T)} \n")
# 等价写法:
print(f"tensor @ tensor.T: \n {tensor @ tensor.T}")

显示:

1
2
3
4
5
6
7
8
9
10
11
tensor.matmul(tensor.T):
 tensor([[3., 3., 3., 3.],
        [3., 3., 3., 3.],
        [3., 3., 3., 3.],
        [3., 3., 3., 3.]])

tensor @ tensor.T:
 tensor([[3., 3., 3., 3.],
        [3., 3., 3., 3.],
        [3., 3., 3., 3.],
        [3., 3., 3., 3.]])

4. 自动赋值运算

自动赋值运算通常在方法后有 _ 作为后缀, 例如: x.copy_(y), x.t_()操作会改变 x 的取值。

1
2
3
print(tensor, "\n")
tensor.add_(5)
print(tensor)

显示:

1
2
3
4
5
6
7
8
9
tensor([[1., 0., 1., 1.],
        [1., 0., 1., 1.],
        [1., 0., 1., 1.],
        [1., 0., 1., 1.]])

tensor([[6., 5., 6., 6.],
        [6., 5., 6., 6.],
        [6., 5., 6., 6.],
        [6., 5., 6., 6.]])

注意:

自动赋值运算虽然可以节省内存, 但在求导时会因为丢失了中间过程而导致一些问题, 所以我们并不鼓励使用它。

4 Tensor与Numpy的转化

张量和Numpy array数组在CPU上可以共用一块内存区域, 改变其中一个另一个也会随之改变。
1. 由张量变换为Numpy array数组

1
2
3
4
t = torch.ones(5)
print(f"t: {t}")
n = t.numpy()
print(f"n: {n}")

显示:

1
2
t: tensor([1., 1., 1., 1., 1.])
n: [1. 1. 1. 1. 1.]

修改张量的值，则Numpy array数组值也会随之改变。

1
2
3
t.add_(1)
print(f"t: {t}")
print(f"n: {n}")

显示:

1
2
t: tensor([2., 2., 2., 2., 2.])
n: [2. 2. 2. 2. 2.]

2. 由Numpy array数组转为张量

1
2
n = np.ones(5)
t = torch.from_numpy(n)

修改Numpy array数组的值，则张量值也会随之改变。

1
2
3
np.add(n, 1, out=n)
print(f"t: {t}")
print(f"n: {n}")

显示:

1
2
t: tensor([2., 2., 2., 2., 2.], dtype=torch.float64)
n: [2. 2. 2. 2. 2.]

三、torch.autograd的简要介绍

torch.autograd是 PyTorch 的自动差分引擎，可为神经网络训练提供支持。 在本节中，您将获得有关 Autograd 如何帮助神经网络训练的概念性理解。

1 背景

神经网络（NN）是在某些输入数据上执行的嵌套函数的集合。 这些函数由参数（由权重和偏差组成）定义，这些参数在 PyTorch 中存储在张量中。

训练 NN 分为两个步骤：

正向传播：在正向传播中，NN 对正确的输出进行最佳猜测。 它通过其每个函数运行输入数据以进行猜测。

反向传播：在反向传播中，NN 根据其猜测中的误差调整其参数。 它通过从输出向后遍历，收集有关函数参数（梯度）的误差导数并使用梯度下降来优化参数来实现。 有关反向传播的更详细的演练，请查看 3Blue1Brown 的视频。

2 在 PyTorch 中的用法

让我们来看一个训练步骤。 对于此示例，我们从torchvision加载了经过预训练的 resnet18 模型。 我们创建一个随机数据张量来表示具有 3 个通道的单个图像，高度&宽度为 64，其对应的label初始化为一些随机值。

1
2
3
4
5
import torch, torchvision
model = torchvision.models.resnet18(pretrained=True)
data = torch.rand(1, 3, 64, 64)
labels = torch.rand(1, 1000)

接下来，我们通过模型的每一层运行输入数据以进行预测。 这是正向传播。

1
2
prediction = model(data) # forward pass

我们使用模型的预测和相应的标签来计算误差（loss）。 下一步是通过网络反向传播此误差。 当我们在误差张量上调用.backward()时，开始反向传播。 然后，Autograd 会为每个模型参数计算梯度并将其存储在参数的.grad属性中。

1
2
3
loss = (prediction - labels).sum()
loss.backward() # backward pass

接下来，我们加载一个优化器，在本例中为 SGD，学习率为 0.01，动量为 0.9。 我们在优化器中注册模型的所有参数。

1
2
optim = torch.optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)

最后，我们调用.step()启动梯度下降。 优化器通过.grad中存储的梯度来调整每个参数。

1
2
optim.step() #gradient descent

至此，您已经具备了训练神经网络所需的一切。 以下各节详细介绍了 Autograd 的工作原理-随时跳过它们。

3 Autograd 的微分

让我们来看看autograd如何收集梯度。 我们用requires_grad=True创建两个张量a和b。 这向autograd发出信号，应跟踪对它们的所有操作。

1
2
3
4
5
import torch

a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)

我们从a和b创建另一个张量Q。

1
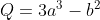
2
Q = 3*a**3 - b**2

假设a和b是神经网络的参数，Q是误差。 在 NN 训练中，我们想要相对于参数的误差，即

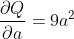
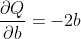
当我们在Q上调用.backward()时，Autograd 将计算这些梯度并将其存储在各个张量的.grad属性中。

我们需要在Q.backward()中显式传递gradient参数，因为它是向量。 gradient是与Q形状相同的张量，它表示Q相对于本身的梯度，即

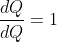
同样，我们也可以将Q聚合为一个标量，然后隐式地向后调用，例如Q.sum().backward()。

1
2
3
external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)

梯度现在沉积在a.grad和b.grad中

1
2
3
4
# check if collected gradients are correct
print(9*a**2 == a.grad)
print(-2*b == b.grad)

出：

1
2
3
tensor([True, True])
tensor([True, True])

可选阅读-使用autograd的向量微积分

从数学上讲，如果您具有向量值函数y = f(x)，则y相对于x的雅可比矩阵J：

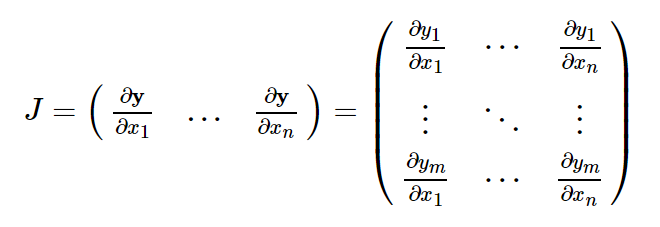
一般来说，torch.autograd是用于计算向量雅可比积的引擎。 也就是说，给定任何向量v，计算乘积J^T · v

如果v恰好是标量函数的梯度

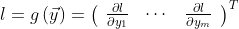
然后根据链式规则，向量-雅可比积将是l相对于x的梯度：

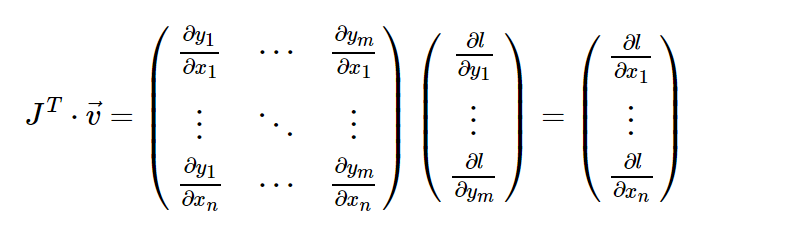
上面的示例中使用的是 vector-Jacobian 乘积的这一特征。 external_grad表示v。

4 计算图

从概念上讲，Autograd 在由函数对象组成的有向无环图（DAG）中记录数据（张量）和所有已执行的操作（以及由此产生的新张量）。 在此 DAG 中，叶子是输入张量，根是输出张量。 通过从根到叶跟踪此图，可以使用链式规则自动计算梯度。

在正向传播中，Autograd 同时执行两项操作：

  • 运行请求的操作以计算结果张量，并且
  • 在 DAG 中维护操作的梯度函数。

当在 DAG 根目录上调用.backward()时，后退通道开始。 autograd然后：

  • 从每个.grad_fn计算梯度，
  • 将它们累积在各自的张量的.grad属性中，然后
  • 使用链式规则，一直传播到叶子张量。

下面是我们示例中 DAG 的直观表示。 在图中，箭头指向前进的方向。 节点代表正向传播中每个操作的反向函数。 蓝色的叶节点代表我们的叶张量a和b。

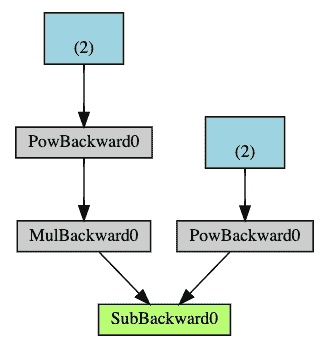
../../_img/dag_autograd.png

注意

DAG 在 PyTorch 中是动态的。要注意的重要一点是，图是从头开始重新创建的； 在每个.backward()调用之后，Autograd 开始填充新图。 这正是允许您在模型中使用控制流语句的原因。 您可以根据需要在每次迭代中更改形状，大小和操作。

从 DAG 中排除

torch.autograd跟踪所有将其requires_grad标志设置为True的张量的操作。 对于不需要梯度的张量，将此属性设置为False会将其从梯度计算 DAG 中排除。

即使只有一个输入张量具有requires_grad=True，操作的输出张量也将需要梯度。

1
2
3
4
5
6
7
8
9
x = torch.rand(5, 5)
y = torch.rand(5, 5)
z = torch.rand((5, 5), requires_grad=True)

a = x + y
print(f"Does `a` require gradients? : {a.requires_grad}")
b = x + z
print(f"Does `b` require gradients?: {b.requires_grad}")

出：

1
2
3
Does `a` require gradients? : False
Does `b` require gradients?: True

在 NN 中，不计算梯度的参数通常称为冻结参数。 如果事先知道您不需要这些参数的梯度，则“冻结”模型的一部分很有用（通过减少自动梯度计算，这会带来一些表现优势）。

从 DAG 中排除很重要的另一个常见用例是调整预训练网络

在微调中，我们冻结了大部分模型，通常仅修改分类器层以对新标签进行预测。 让我们来看一个小例子来说明这一点。 和以前一样，我们加载一个预训练的 resnet18 模型，并冻结所有参数。

1
2
3
4
5
6
7
8
from torch import nn, optim

model = torchvision.models.resnet18(pretrained=True)

# Freeze all the parameters in the network
for param in model.parameters():
    param.requires_grad = False

假设我们要在具有 10 个标签的新数据集中微调模型。 在 resnet 中，分类器是最后一个线性层model.fc。 我们可以简单地将其替换为充当我们的分类器的新线性层（默认情况下未冻结）。

1
2
model.fc = nn.Linear(512, 10)

现在，除了model.fc的参数外，模型中的所有参数都将冻结。 计算梯度的唯一参数是model.fc的权重和偏差。

1
2
3
# Optimize only the classifier
optimizer = optim.SGD(model.fc.parameters(), lr=1e-2, momentum=0.9)

请注意，尽管我们在优化器中注册了所有参数，但唯一可计算梯度的参数（因此会在梯度下降中进行更新）是分类器的权重和偏差。

torch.no_grad()中的上下文管理器可以使用相同的排除功能。

四、神经网络

可以使用torch.nn包构建神经网络。

现在您已经了解了autograd，nn依赖于autograd来定义模型并对其进行微分。 nn.Module包含层，以及返回output的方法forward(input)。

例如，查看以下对数字图像进行分类的网络：

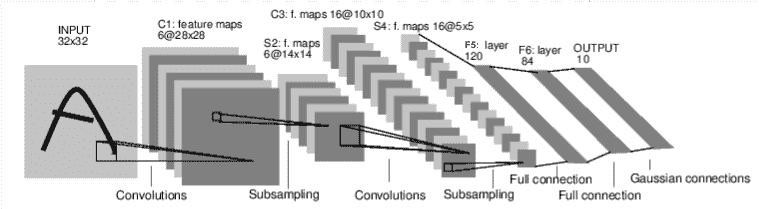
convnet

卷积网

这是一个简单的前馈网络。 它获取输入，将其一层又一层地馈入，然后最终给出输出。

神经网络的典型训练过程如下：

  • 定义具有一些可学习参数（或权重）的神经网络
  • 遍历输入数据集，进行数据预处理
  • 通过网络处理输入，进行正向传播
  • 计算损失（输出正确的距离有多远）
  • 将梯度传播回网络参数
  • 通常使用简单的更新规则来更新网络的权重：weight = weight - learning_rate * gradient

1 定义网络

让我们定义这个网络：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import torch
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 3x3 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 3)
        self.conv2 = nn.Conv2d(6, 16, 3)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 6 * 6, 120)  # 6*6 from image dimension
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features

net = Net()
print(net)

出：

1
2
3
4
5
6
7
8
Net(
  (conv1): Conv2d(1, 6, kernel_size=(3, 3), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(3, 3), stride=(1, 1))
  (fc1): Linear(in_features=576, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

您只需要定义forward函数，就可以使用autograd为您自动定义backward函数（计算梯度）。 您可以在forward函数中使用任何张量操作。

模型的可学习参数由net.parameters()返回

1
2
3
4
params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight

出：

1
2
3
10
torch.Size([6, 1, 3, 3])

让我们尝试一个32x32随机输入。 注意：该网络的预期输入大小（LeNet）为32x32。 要在 MNIST 数据集上使用此网络，请将图像从数据集中调整为32x32。

1
2
3
4
input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

出：

1
2
3
tensor([[ 0.1002, -0.0694, -0.0436,  0.0103,  0.0488, -0.0429, -0.0941, -0.0146,
         -0.0031, -0.0923]], grad_fn=<AddmmBackward>)

使用随机梯度将所有参数和反向传播的梯度缓冲区归零：

1
2
3
net.zero_grad()
out.backward(torch.randn(1, 10))

注意

torch.nn仅支持小批量。 整个torch.nn包仅支持作为微型样本而不是单个样本的输入。

例如，nn.Conv2d将采用nSamples x nChannels x Height x Width的 4D 张量。

如果您只有一个样本，只需使用input.unsqueeze(0)添加一个假批量尺寸。

在继续之前，让我们回顾一下到目前为止所看到的所有类。

回顾：

  • torch.Tensor-一个多维数组，支持诸如backward()的自动微分操作。 同样，保持相对于张量的梯度。
  • nn.Module-神经网络模块。 封装参数的便捷方法，并带有将其移动到 GPU，导出，加载等的帮助器。
  • nn.Parameter-一种张量，即将其分配为Module的属性时，自动注册为参数。
  • autograd.Function-实现自动微分操作的正向和反向定义。 每个Tensor操作都会创建至少一个Function节点，该节点连接到创建Tensor的函数，并且编码其历史记录。

目前为止，我们涵盖了：

  • 定义神经网络
  • 处理输入并向后调用

仍然剩下：

  • 计算损失
  • 更新网络的权重

2 损失函数

损失函数采用一对（输出，目标）输入，并计算一个值，该值估计输出与目标之间的距离。

nn包下有几种不同的损失函数。 一个简单的损失是：nn.MSELoss，它计算输入和目标之间的均方误差。

例如：

1
2
3
4
5
6
7
8
output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

出：

1
2
tensor(0.4969, grad_fn=<MseLossBackward>)

现在，如果使用.grad_fn属性向后跟随loss，您将看到一个计算图，如下所示：

1
2
3
4
5
input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> view -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss

因此，当我们调用loss.backward()时，整个图将被微分。 损失，并且图中具有requires_grad=True的所有张量将随梯度累积其.grad张量。

为了说明，让我们向后走几步：

1
2
3
4
print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

出：

1
2
3
4
<MseLossBackward object at 0x7f1ba05a1ba8>
<AddmmBackward object at 0x7f1ba05a19e8>
<AccumulateGrad object at 0x7f1ba05a19e8>

3 反向传播

要反向传播误差，我们要做的只是对loss.backward()。 不过，您需要清除现有的梯度，否则梯度将累积到现有的梯度中。

现在，我们将其称为loss.backward()，然后看一下向后前后conv1的偏差梯度。

1
2
3
4
5
6
7
8
9
10
net.zero_grad()     # zeroes the gradient buffers of all parameters

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

出：

1
2
3
4
5
conv1.bias.grad before backward
tensor([0., 0., 0., 0., 0., 0.])
conv1.bias.grad after backward
tensor([ 0.0111, -0.0064,  0.0053, -0.0047,  0.0026, -0.0153])

现在，我们已经看到了如何使用损失函数。

稍后阅读：

神经网络包包含各种模块和损失函数，这些模块和损失函数构成了深度神经网络的构建块。 带有文档的完整列表位于此处。

唯一需要学习的是：

  • 更新网络的权重

4 更新权重

实践中使用的最简单的更新规则是随机梯度下降（SGD）：

weight = weight - learning_rate * gradient

我们可以使用简单的 Python 代码实现此目标：

1
2
3
4
learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

但是，在使用神经网络时，您希望使用各种不同的更新规则，例如 SGD，Nesterov-SGD，Adam，RMSProp 等。为实现此目的，我们构建了一个小包装：torch.optim，可实现所有这些方法。 使用它非常简单：

1
2
3
4
5
6
7
8
9
10
11
12
import torch.optim as optim

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop:
optimizer.zero_grad()   # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update

注意

观察如何使用optimizer.zero_grad()将梯度缓冲区手动设置为零。 这是因为如反向传播部分中所述累积了梯度。

五、图像分类器

就是这个。 您已经了解了如何定义神经网络，计算损失并更新网络的权重。

现在您可能在想，

1 数据获取

通常，当您必须处理图像，文本，音频或视频数据时，可以使用将数据加载到 NumPy 数组中的标准 Python 包。 然后，您可以将该数组转换为torch.*Tensor。

  • 对于图像，Pillow，OpenCV 等包很有用
  • 对于音频，请使用 SciPy 和 librosa 等包
  • 对于文本，基于 Python 或 Cython 的原始加载，或者 NLTK 和 SpaCy 很有用

专门针对视觉，我们创建了一个名为torchvision的包，其中包含用于常见数据集（例如 Imagenet，CIFAR10，MNIST 等）的数据加载器，以及用于图像（即torchvision.datasets和torch.utils.data.DataLoader）的数据转换器。

这提供了极大的便利，并且避免了编写样板代码。

在本教程中，我们将使用 CIFAR10 数据集。 它具有以下类别：“飞机”，“汽车”，“鸟”，“猫”，“鹿”，“狗”，“青蛙”，“马”，“船”，“卡车”。 CIFAR-10 中的图像尺寸为3x32x32，即尺寸为32x32像素的 3 通道彩色图像。

cifar10

cifar10

2 训练图像分类器

我们将按顺序执行以下步骤：

  1. 使用torchvision加载并标准化 CIFAR10 训练和测试数据集
  2. 定义卷积神经网络
  3. 定义损失函数
  4. 根据训练数据训练网络
  5. 在测试数据上测试网络

1.加载并标准化 CIFAR10

使用torchvision，加载 CIFAR10 非常容易。

1
2
3
4
import torch
import torchvision
import torchvision.transforms as transforms

TorchVision 数据集的输出是[0, 1]范围的PILImage图像。 我们将它们转换为归一化范围[-1, 1]的张量。 .. 注意：

1
2
3
If running on Windows and you get a BrokenPipeError, try setting
the num_worker of torch.utils.data.DataLoader() to 0.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
transform = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                        download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
                                          shuffle=True, num_workers=2)

testset = torchvision.datasets.CIFAR10(root='./data', train=False,
                                       download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4,
                                         shuffle=False, num_workers=2)

classes = ('plane', 'car', 'bird', 'cat',
           'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

出：

1
2
3
4
Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to ./data/cifar-10-python.tar.gz
Extracting ./data/cifar-10-python.tar.gz to ./data
Files already downloaded and verified

让我们展示一些训练图像，很有趣。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import matplotlib.pyplot as plt
import numpy as np

# functions to show an image

def imshow(img):
    img = img / 2 + 0.5     # unnormalize
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))
    plt.show()

# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()

# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))

../../_img/sphx_glr_cifar10_tutorial_001.png

出：

1
2
dog truck  frog horse

2.定义卷积神经网络

之前从“神经网络”部分复制神经网络，然后对其进行修改以获取 3 通道图像（而不是定义的 1 通道图像）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

net = Net()

3.定义损失函数和优化器

让我们使用分类交叉熵损失和带有动量的 SGD。

1
2
3
4
5
import torch.optim as optim

criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)

4.训练网络

这是事情开始变得有趣的时候。 我们只需要遍历数据迭代器，然后将输入馈送到网络并进行优化即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
for epoch in range(2):  # loop over the dataset multiple times

    running_loss = 0.0
    for i, data in enumerate(trainloader, 0):
        # get the inputs; data is a list of [inputs, labels]
        inputs, labels = data

        # zero the parameter gradients
        optimizer.zero_grad()

        # forward + backward + optimize
        outputs = net(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()

        # print statistics
        running_loss += loss.item()
        if i % 2000 == 1999:    # print every 2000 mini-batches
            print('[%d, %5d] loss: %.3f' %
                  (epoch + 1, i + 1, running_loss / 2000))
            running_loss = 0.0

print('Finished Training')

出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
[1,  2000] loss: 2.196
[1,  4000] loss: 1.849
[1,  6000] loss: 1.671
[1,  8000] loss: 1.589
[1, 10000] loss: 1.547
[1, 12000] loss: 1.462
[2,  2000] loss: 1.382
[2,  4000] loss: 1.389
[2,  6000] loss: 1.369
[2,  8000] loss: 1.332
[2, 10000] loss: 1.304
[2, 12000] loss: 1.288
Finished Training

让我们快速保存我们训练过的模型：

1
2
3
PATH = './cifar_net.pth'
torch.save(net.state_dict(), PATH)

有关保存 PyTorch 模型的更多详细信息，请参见此处。

5.根据测试数据测试网络

我们已经在训练数据集中对网络进行了 2 次训练。 但是我们需要检查网络是否学到了什么。

我们将通过预测神经网络输出的类别标签并根据实际情况进行检查来进行检查。 如果预测正确，则将样本添加到正确预测列表中。

好的，第一步。 让我们显示测试集中的图像以使其熟悉。

1
2
3
4
5
6
7
dataiter = iter(testloader)
images, labels = dataiter.next()

# print images
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))

../../_img/sphx_glr_cifar10_tutorial_002.png

出：

1
2
GroundTruth:    cat  ship  ship plane

接下来，让我们重新加载保存的模型（注意：这里不需要保存和重新加载模型，我们只是为了说明如何这样做）：

1
2
3
net = Net()
net.load_state_dict(torch.load(PATH))

好的，现在让我们看看神经网络对以上这些示例的看法：

1
2
outputs = net(images)

输出是 10 类的能量。 一个类别的能量越高，网络就认为该图像属于特定类别。 因此，让我们获取最高能量的指数：

1
2
3
4
5
_, predicted = torch.max(outputs, 1)

print('Predicted: ', ' '.join('%5s' % classes[predicted[j]]
                              for j in range(4)))

出：

1
2
Predicted:    cat  ship  ship plane

结果似乎还不错。

让我们看一下网络在整个数据集上的表现。

1
2
3
4
5
6
7
8
9
10
11
12
13
correct = 0
total = 0
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print('Accuracy of the network on the 10000 test images: %d %%' % (
    100 * correct / total))

出：

1
2
Accuracy of the network on the 10000 test images: 53 %

看起来比偶然更好，准确率是 10%（从 10 个类中随机选择一个类）。 好像网络学到了一些东西。

嗯，哪些类的表现良好，哪些类的表现不佳：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class_correct = list(0\. for i in range(10))
class_total = list(0\. for i in range(10))
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs, 1)
        c = (predicted == labels).squeeze()
        for i in range(4):
            label = labels[i]
            class_correct[label] += c[i].item()
            class_total[label] += 1

for i in range(10):
    print('Accuracy of %5s : %2d %%' % (
        classes[i], 100 * class_correct[i] / class_total[i]))

出：

1
2
3
4
5
6
7
8
9
10
11
Accuracy of plane : 50 %
Accuracy of   car : 62 %
Accuracy of  bird : 51 %
Accuracy of   cat : 32 %
Accuracy of  deer : 31 %
Accuracy of   dog : 35 %
Accuracy of  frog : 77 %
Accuracy of horse : 70 %
Accuracy of  ship : 71 %
Accuracy of truck : 52 %

好的，那下一步呢？

我们如何在 GPU 上运行这些神经网络？

3 在 GPU 上进行训练

就像将张量转移到 GPU 上一样，您也将神经网络转移到 GPU 上。

如果可以使用 CUDA，首先将我们的设备定义为第一个可见的 cuda 设备：

1
2
3
4
5
6
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# Assuming that we are on a CUDA machine, this should print a CUDA device:

print(device)

出：

1
2
cuda:0

本节的其余部分假定device是 CUDA 设备。

然后，这些方法将递归遍历所有模块，并将其参数和缓冲区转换为 CUDA 张量：

1
2
net.to(device)

请记住，您还必须将每一步的输入和目标也发送到 GPU：

1
2
inputs, labels = data[0].to(device), data[1].to(device)

与 CPU 相比，为什么我没有注意到 MASSIVE 加速？ 因为您的网络真的很小。

练习：尝试增加网络的宽度（第一个nn.Conv2d的参数 2 和第二个nn.Conv2d的参数 1 –它们必须是相同的数字），看看您可以得到哪种加速。

已实现的目标：

  • 全面了解 PyTorch 的张量库和神经网络。
  • 训练一个小型神经网络对图像进行分类

4 在多个 GPU 上进行训练

如果您想使用所有 GPU 来获得更大的大规模加速，请查看可选：数据并行。