25_Support Vector Machine
Support Vector Machine
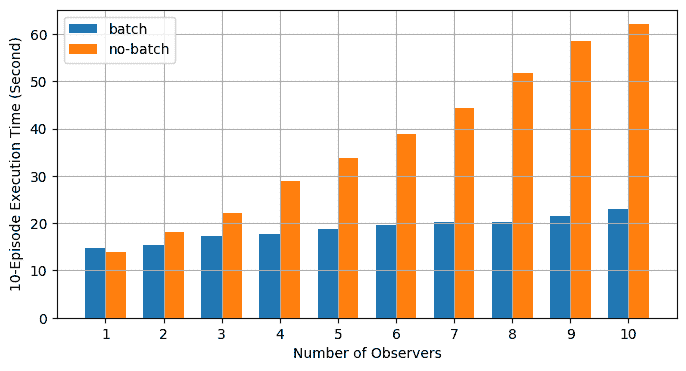
支持向量机(SVM)有两个特点:SVM=铰链损失(Hinge Loss)+核技巧(Kernel Method)
注:建议先看这篇博客了解SVM基础知识后再看本文的分析
Hinge Loss
Binary Classification
先回顾一下二元分类的做法,为了方便后续推导,这里定义data的标签为-1和+1
当$f(x)>0$时,$g(x)=1$,表示属于第一类别;当$f(x)<0$时,$g(x)=-1$,表示属于第二类别
原本用$\sum \delta(g(x^n)\ne \hat y^n)$,不匹配的样本点个数,来描述loss function,其中$\delta=1$表示$x$与$\hat y$相匹配,反之$\delta=0$,但这个式子不可微分,无法使用梯度下降法更新参数
因此使用近似的可微分的$l(f(x^n),\hat y^n)$来表示损失函数

下图中,横坐标为$\hat y^n f(x)$,我们希望横坐标越大越好:
- 当$\hat y^n>0$时,希望$f(x)$越正越好
- 当$\hat y^n<0$时,希望$f(x)$越负越好
纵坐标是loss,原则上,当横坐标$\hat y^n f(x)$越大的时候,纵坐标loss要越小,横坐标越小,纵坐标loss要越大
ideal loss
在$L(f)=\sum\limits_n \delta(g(x^n)\ne \hat y^n)$的理想情况下,如果$\hat y^n f(x)>0$,则loss=0,如果$\hat y^n f(x)<0$,则loss=1,如下图中加粗的黑线所示,可以看出该曲线是无法微分的,因此我们要另一条近似的曲线来替代该损失函数

square loss
下图中的红色曲线代表了square loss的损失函数:$l(f(x^n),\hat y^n)=(\hat y^n f(x^n)-1)^2$
- 当$\hat y^n=1$时,$f(x)$与1越接近越好,此时损失函数化简为$(f(x^n)-1)^2$
- 当$\hat y^n=-1$时,$f(x)$与-1越接近越好,此时损失函数化简为$(f(x^n)+1)^2$
- 但实际上整条曲线是不合理的,它会使得$\hat y^n f(x)$很大的时候有一个更大的loss

sigmoid+square loss
此外蓝线代表sigmoid+square loss的损失函数:$l(f(x^n),\hat y^n)=(\sigma(\hat y^n f(x^n))-1)^2$
- 当$\hat y^n=1$时,$\sigma (f(x))$与1越接近越好,此时损失函数化简为$(\sigma(f(x))-1)^2$
- 当$\hat y^n=-1$时,$\sigma (f(x))$与0越接近越好,此时损失函数化简为$(\sigma(f(x)))^2$
- 在逻辑回归的时候实践过,一般square loss的方法表现并不好,而是用cross entropy会更好
sigmoid+cross entropy
绿线则是代表了sigmoid+cross entropy的损失函数:$l(f(x^n),\hat y^n)=ln(1+e^{-\hat y^n f(x)})$
- $\sigma (f(x))$代表了一个分布,而Ground Truth则是真实分布,这两个分布之间的交叉熵,就是我们要去minimize的loss
- 当$\hat y^n f(x)$很大的时候,loss接近于0
- 当$\hat y^n f(x)$很小的时候,loss特别大
- 下图是把损失函数除以$ln2$的曲线,使之变成ideal loss的upper bound,且不会对损失函数本身产生影响
- 我们虽然不能minimize理想的loss曲线,但我们可以minimize它的upper bound,从而起到最小化loss的效果

cross entropy VS square error
为什么cross entropy要比square error要来的有效呢?
我们期望在极端情况下,比如$\hat y^n$与$f(x)$非常不匹配导致横坐标非常负的时候,loss的梯度要很大,这样才能尽快地通过参数调整回到loss低的地方
对sigmoid+square loss来说,当横坐标非常负的时候,loss的曲线反而是平缓的,此时去调整参数值对最终loss的影响其实并不大,它并不能很快地降低
形象来说就是,“没有回报,不想努力”
而对cross entropy来说,当横坐标非常负的时候,loss的梯度很大,稍微调整参数就可以往loss小的地方走很大一段距离,这对训练是友好的
形象来说就是,“努力可以有回报””
Hinge Loss
紫线代表了hinge loss的损失函数:$l(f(x^n),\hat y^n)=\max(0,1-\hat y^n f(x))$
- 当$\hat y^n=1$,损失函数化简为$\max(0,1-f(x))$
- 此时只要$f(x)>1$,loss就会等于0
- 当$\hat y^n=-1$,损失函数化简为$\max(0,1+f(x))$
- 此时只要$f(x)<-1$,loss就会等于0
- 总结一下,如果label为1,则当$f(x)>1$,机器就认为loss为0;如果label为-1,则当$f(x)<-1$,机器就认为loss为0,因此该函数并不需要$f(x)$有一个很大的值

在紫线中,当$\hat y^n f(x)>1$,则已经实现目标,loss=0;当$\hat y^n f(x)>0$,表示已经得到了正确答案,但Hinge Loss认为这还不够,它需要你继续往1的地方前进
事实上,Hinge Loss也是Ideal loss的upper bound,但是当横坐标$\hat y^n f(x)>1$时,它与Ideal loss近乎是完全贴近的
比较Hinge loss和cross entropy,最大的区别在于他们对待已经做得好的样本点的态度,在横坐标$\hat y^n f(x)>1$的区间上,cross entropy还想要往更大的地方走,而Hinge loss则已经停下来了,就像一个的目标是”还想要更好“,另一个的目标是”及格就好“
在实作上,两者差距并不大,而Hinge loss的优势在于它不怕outlier,训练出来的结果鲁棒性(robust)比较强
Linear SVM
model description
在线性的SVM里,我们把$f(x)=\sum\limits_i w_i x_i+b=w^Tx$看做是向量$\left [\begin{matrix}w\b \end{matrix}\right ]$和向量$\left [\begin{matrix}x\1 \end{matrix}\right ]$的内积,也就是新的$w$和$x$,这么做可以把bias项省略掉
在损失函数中,我们通常会加上一个正规项,即$L(f)=\sum\limits_n l(f(x^n),\hat y^n)+\lambda ||w||_2$
这是一个convex的损失函数,好处在于无论从哪个地方开始做梯度下降,最终得到的结果都会在最低处,曲线中一些折角处等不可微的点可以参考NN中relu、maxout等函数的微分处理

对比Logistic Regression和Linear SVM,两者唯一的区别就是损失函数不同,前者用的是cross entropy,后者用的是Hinge loss
事实上,SVM并不局限于Linear,尽管Linear可以带来很多好的特质,但我们完全可以在一个Deep的神经网络中使用Hinge loss的损失函数,就成为了Deep SVM,其实Deep Learning、SVM这些方法背后的精神都是相通的,并没有那么大的界限
gradient descent
尽管SVM大多不是用梯度下降训练的,但使用该方法训练确实是可行的,推导过程如下:

another formulation
前面列出的式子可能与你平常看到的SVM不大一样,这里将其做一下简单的转换
对$L(f)=\sum\limits_n \max(0,1-\hat y^n f(x))+\lambda ||w||_2$,用$L(f)=\sum\limits_n \epsilon^n+\lambda ||w||_2$来表示
其中$\epsilon^n=\max(0,1-\hat y^n f(x))$
对$\epsilon^n\geq0$、$\epsilon^n\geq1-\hat y^n f(x)$来说,它与上式原本是不同的,因为max是二选一,而$\geq$则取到等号的限制
但是当加上取loss function $L(f)$最小化这个条件时,$\geq$就要取到等号,两者就是等价的

此时该表达式就和你熟知的SVM一样了:
$L(f)=\sum\limits_n \epsilon^n+\lambda ||w||_2$,且$\hat y^n f(x)\geq 1-\epsilon^n$,其中$\hat y^n$和$f(x)$要同号,$\epsilon^n$要大于等于0,这里$\epsilon^n$的作用就是放宽1的margin,也叫作松弛变量(slack variable)
这是一个QP问题(Quadradic programming problem),可以用对应方法求解,当然前面提到的梯度下降法也可以解
Kernel Method
explain linear combination
你要先说服你自己一件事:实际上我们找出来的可以minimize损失函数的参数,其实就是data的线性组合
$$
w^=\sum\limits_n \alpha^_n x^n
$$
你可以通过拉格朗日乘数法去求解前面的式子来验证,这里试图从梯度下降的角度来解释:
观察$w$的更新过程$w=w-\eta\sum\limits_n c^n(w)x^n$可知,如果$w$被初始化为0,则每次更新的时候都是加上data point $x$的线性组合,因此最终得到的$w$依旧会是$x$的Linear Combination
而使用Hinge loss的时候,$c^n(w)$往往会是0,不是所有的$x^n$都会被加到$w$里去,而被加到$w$里的那些$x^n$,就叫做support vector

SVM解出来的$\alpha_n$是sparse的,因为有很多$x^n$的系数微分为0,这意味着即使从数据集中把这些$x^n$的样本点移除掉,对结果也是没有影响的,这可以增强系统的鲁棒性;而在传统的cross entropy的做法里,每一笔data对结果都会有影响,因此鲁棒性就没有那么好
redefine model and loss function
知道$w$是$x^n$的线性组合之后,我们就可以对原先的SVM函数进行改写:
$$
w=\sum_n\alpha_nx^n=X\alpha \
f(x)=w^Tx=\alpha^TX^Tx=\sum_n\alpha_n(x^n\cdot x)
$$
这里的$x$表示新的data,$x^n$表示数据集中已存在的所有data,由于很多$\alpha_n$为0,因此计算量并不是很大

接下来把$x^n$与$x$的内积改写成Kernel function的形式:$x^n\cdot x=K(x^n,x)$
此时model就变成了$f(x)= \sum\limits_n\alpha_n K(x^n,x)$,未知的参数变成了$\alpha_n$
现在我们的目标是,找一组最好的$\alpha_n$,让loss最小,此时损失函数改写为:
$$
L(f)=\sum\limits_n l(\sum\limits_{n’} \alpha_{n’}K(x^{n’},x^n),\hat y^n)
$$
从中可以看出,我们并不需要真的知道$x$的vector是多少,需要知道的只是$x$跟$z$之间的内积值$K(x,z)$,也就是说,只要知道Kernel function $K(x,z)$,就可以去对参数做优化了,这招就叫做Kernel Trick

Kernel Trick
linear model会有很多的限制,有时候需要对输入的feature做一些转换之后,才能用linear model来处理,假设现在我们的data是二维的,$x=\left[ \begin{matrix}x_1\x_2 \end{matrix} \right]$,先要对它做feature transform,然后再去应用Linear SVM
如果要考虑特征之间的关系,则把特征转换为$\phi(x)=\left[ \begin{matrix}x_1^2\\sqrt{2}x_1x_2\ x_2^2 \end{matrix} \right]$,此时Kernel function就变为:
$$
K(x,z)=\phi(x)\cdot \phi(z)=\left[ \begin{matrix}x_1^2\\sqrt{2}x_1x_2\ x_2^2 \end{matrix} \right] \cdot \left[ \begin{matrix}z_1^2\\sqrt{2}z_1z_2\ z_2^2 \end{matrix} \right]=(x_1z_1+x_2z_2)^2=(\left[ \begin{matrix}x_1\x_2 \end{matrix} \right]\cdot \left[ \begin{matrix}z_1\z_2 \end{matrix} \right])^2=(x\cdot z)^2
$$

可见,我们对$x$和$z$做特征转换+内积,就等同于在原先的空间上先做内积再平方,在高维空间里,这种方式可以有更快的速度和更小的运算量

RBF Kernel
在RBF Kernel中,$K(x,z)=e^{-\frac{1}{2}||x-z||_2}$,实际上也可以表示为$\phi(x)\cdot \phi(z)$,只不过$\phi(*)$的维数是无穷大的,所以我们直接使用Kernel trick计算,其实就等同于在无穷多维的空间中计算两个向量的内积
将Kernel展开成无穷维如下:

把与$x$相关的无穷多项串起来就是$\phi(x)$,把与$z$相关的无穷多项串起来就是$\phi(z)$,也就是说,当你使用RBF Kernel的时候,实际上就是在无穷多维的平面上做事情,当然这也意味着很容易过拟合
Sigmoid Kernel
Sigmoid Kernel:$K(x,z)=\tanh(x,z)$
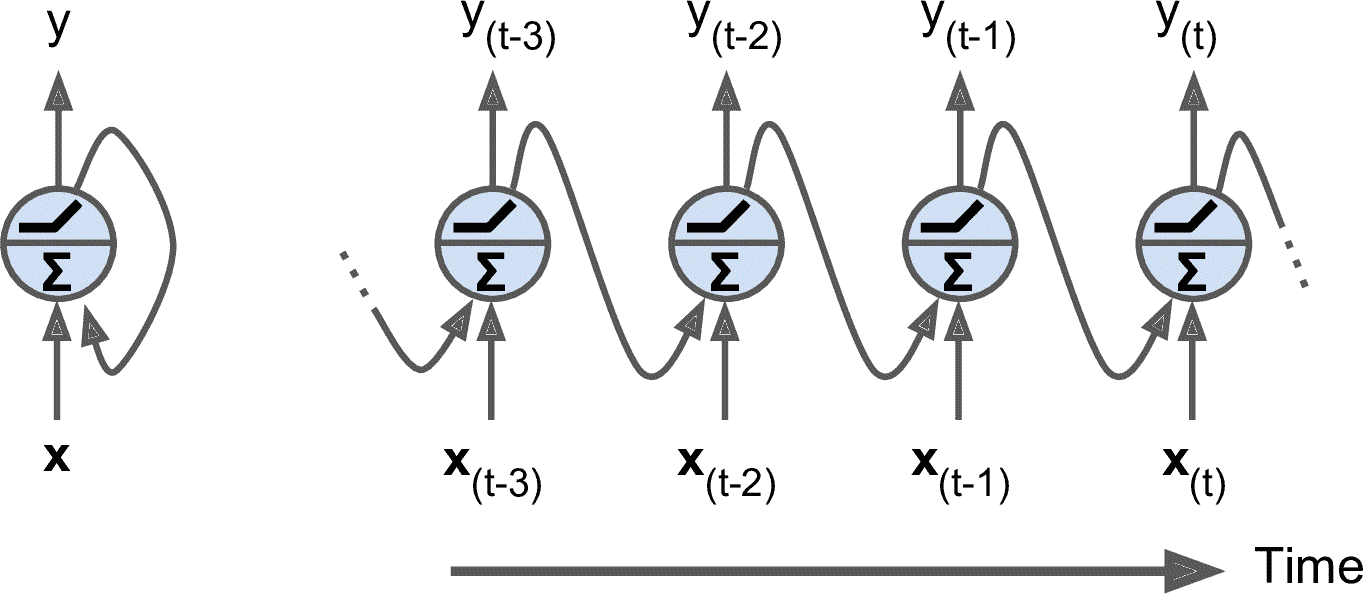
如果使用的是Sigmoid Kernel,那model $f(x)$就可以被看作是只有一层hidden layer的神经网络,其中$x^1$~$x^n$可以被看作是neuron的weight,变量$x$乘上这些weight,再通过tanh激活函数,最后全部乘上$\alpha^1$~$\alpha^n$做加权和,得到最后的$f(x)$

其中neuron的数目,由support vector的数量决定
Design Kernel Function
既然有了Kernel Trick,其实就可以直接去设计Kernel Function,它代表了投影到高维以后的内积,类似于相似度的概念
我们完全可以不去管$x$和$z$的特征长什么样,因为用低维的$x$和$z$加上$K(x,z)$,就可以直接得到高维空间中$x$和$z$经过转换后的内积,这样就省去了转换特征这一步
当$x$是一个有结构的对象,比如不同长度的sequence,它们其实不容易被表示成vector,我们不知道$x$的样子,就更不用说$\phi(x)$了,但是只要知道怎么计算两者之间的相似度,就有机会把这个Similarity当做Kernel来使用
我们随便定义一个Kernel Function,其实并不一定能够拆成两个向量内积的结果,但有Mercer’s theory可以帮助你判断当前的function是否可拆分
下图是直接定义语音vector之间的相似度$K(x,z)$来做Kernel Trick的示例:

SVM vs Deep Learning
这里简单比较一下SVM和Deep Learning的差别:
deep learning的前几层layer可以看成是在做feature transform,而后几层layer则是在做linear classifier
SVM也类似,先用Kernel Function把feature transform到高维空间上,然后再使用linear classifier
在SVM里一般Linear Classifier都会采用Hinge Loss