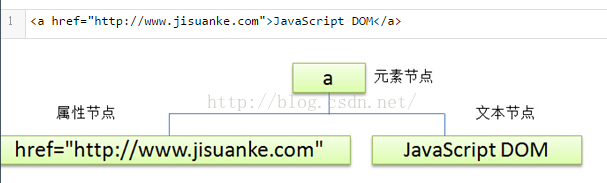
6.5 B树

B树

1 简介

概念

• B 树又叫平衡多路查找树。一棵m阶的B树定义如下：

  1. B树中的每个节点最多包含m个子节点。最多包含m-1个键。
  2. 除根节点和叶节点外，B树中的每个节点至少包含[m/2]（向上取整）个子节点。
  3. 根节点要么是空、要么是独自的根、要么必须至少有2个子节点。
  4. 有k个子节点的节点必有k-1个键。每个键按顺序升序排序。
  5. 所有叶节点必须处于同一层（水平）。

• 4阶B树如下

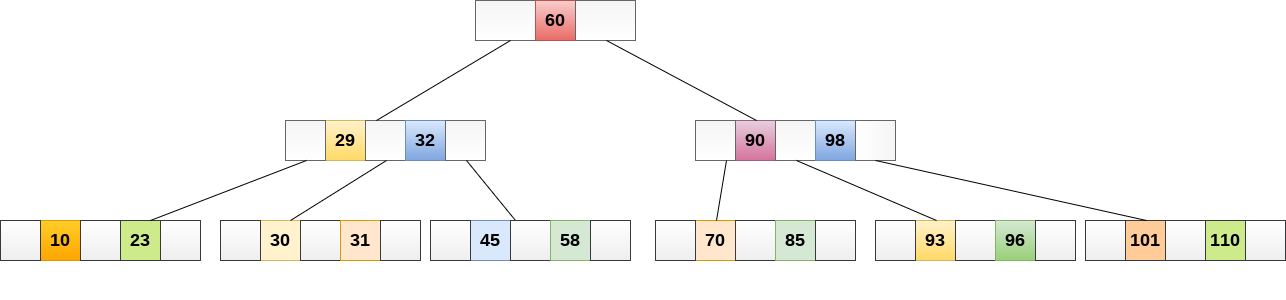
应用

• 大规模数据存储中，二叉树节点存储的元素数量是有限的（如果元素数量非常多的话，查找就退化成节点内部的线性查找了），这样导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁，进而导致查询效率低下
• 如何减少树的深度，一个基本的想法就是：采用多叉树结构（由于树节点元素数量是有限的，自然该节点的子树数量也就是有限的）。
• 多路查找树。根据平衡二叉树的启发，使用平衡多路查找树结构，也就是这篇文章所要阐述的第一个Btree。

分类

• B树
• B+树
• B*树

2 操作

基础操作

• 创建
• 遍历和搜索
• 插入
• 删除
• 分裂
• 合并

创建

搜索

B树中搜索类似于二叉搜索树中的搜索

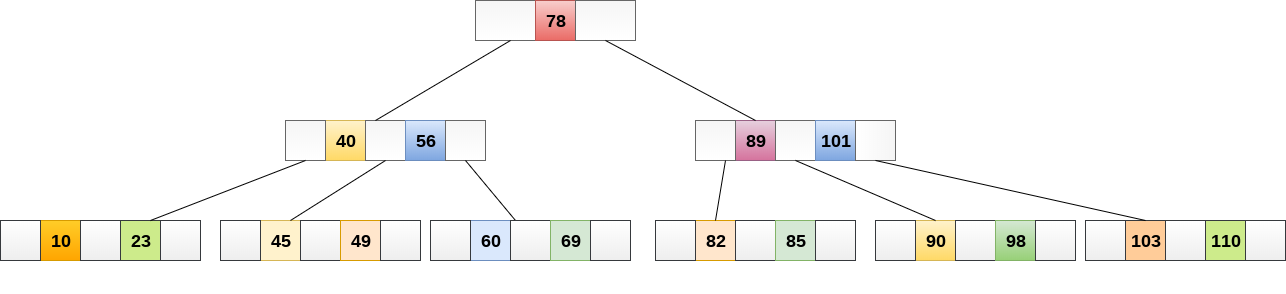
• 将数据项49与根节点78进行比较。
• 因为49 <78因此，移动到其左子树。
• 因为，40 <49 <56，遍历中间子树40。49> 45，向右移动。
• 比较49。找到匹配，则返回。

在B树中搜索取决于树的高度。 搜索算法需要O(log n)时间来搜索B树中的任何元素。

插入

• 遍历B树以找到可插入节点的适当叶节点。
• 如果叶节点包含少于m-1个键，则按递增顺序插入元素。
• 否则，如果叶节点包含m-1个键，则按照以下步骤操作。
  • 按元素的递增顺序插入新元素。
  • 将节点从中间拆分为的两个节点。
  • 将中值元素推送到其父节点。
  • 如果父节点还包含m-1个键，则按照相同的步骤将其拆分。

实例

• 将节点8插入到下图所示的5阶B树中。
  
• 8将插入5的右侧，因此插入8。
  
• 该节点现在包含5个键，大于(5 -1 = 4)个键。 因此，将节点从中间分开，即8，并将其推到其父节点，如下所示。（图有问题）
  

删除

• 找到叶节点。
• 如果叶节点中有多于m/2个键，则从节点中删除所需的键。
• 如果叶节点不包含m/2个键，则通过从8个或左兄弟中获取元素来完成键。
  • 如果左侧兄弟包含多于m/2个元素，则将其最大元素推送到其父元素，并将插入元素向下移动到删除键的节点。
  • 如果右侧兄弟包含多于m/2个元素，则将其最小元素向上推送到父节点，并将插入元素向下移动到删除键的节点。
  • 如果兄弟节点都不包含多于m/2个元素，则通过连接两个叶节点和父节点的插入元素来创建新的叶节点。
  • 如果父节点的节点少于m/2，那么也应在父节点上应用上述过程。
• 如果要删除的节点是内部节点，则将节点替换为其有序后继或前一个节点。 由于后继或前任将始终位于叶节点上，因此该过程将类似于从叶节点中删除节点。

实例

• 从下图所示的5阶B树中删除节点：53。
  
• 元素49的右子节点中存在53，则删除它。
  
• 现在，57是唯一留在节点中的元素，在5阶B树中必须存在的最小元素数是2。它小于左边和右边子树中的元素 因此，也不足以将其与父母的左兄弟和干预元素合并，即49。最终的B树如下所示。
  

实现