Estom的博客

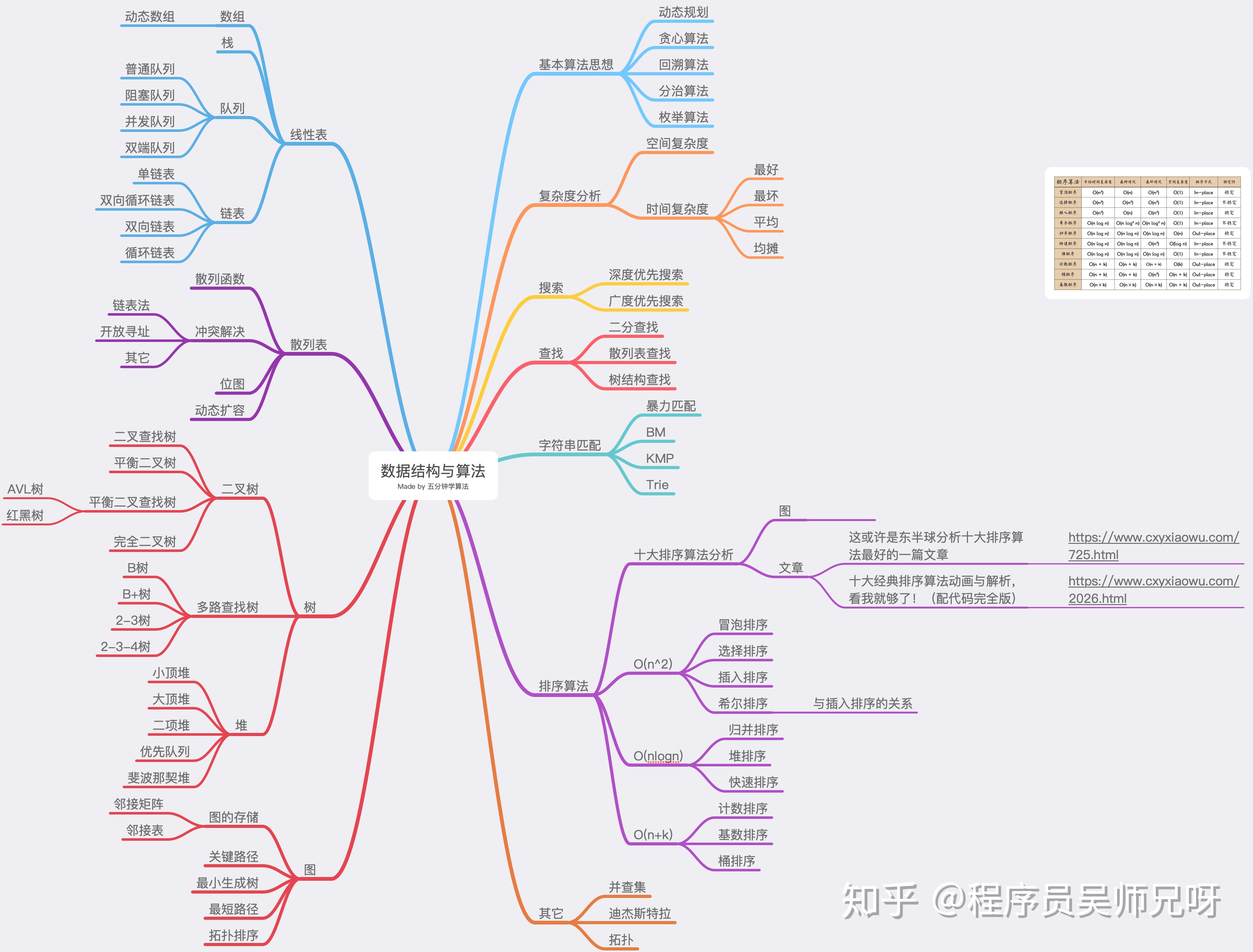
数据结构基础 参考文献 易佰教程 1 简介数据结构的组成 数据结构主要包括两部分。 数据的结构。包括存储结构和逻辑结构。存储结构决定在其在计算机内存中的表现形式和具有的特点。逻辑结构决定了“数据”内部之间的关联结构。 数据的规则。基于数据的存储结构和逻辑结构。衍生出数据的一系列基本操作。包括创建、遍历、插入、删除等，每一类数据结构都有其相应的基础操作。 本目录主要讲解了。数据的结构和数据的规则。以及这两个东西的实现方法。不包括在这些数据的和数据的规则之上的更顶层的算法。如基于前序遍历（数据的规则）的什么什么算法（上层的算法）。 数据结构预算法 基本术语数据结构是任何程序或软件的构建块(基础块)。为程序选择适当的数据结构对于程序员来说是最困难的任务。就数据结构而言，使用以下术语 - 数据：数据可以定义为基本值或值集合，例如，学生的姓名和ID，成绩等就是学生的数据。 组项：具有从属数据项的数据项称为组项，例如，学生的姓名由名字和姓氏组成。 记录：记录可以定义为各种数据项的集合，例如，如果以学生实体为例，那么学生的名称，地址，课程和标记可以组合在一起形成学生的记录。...

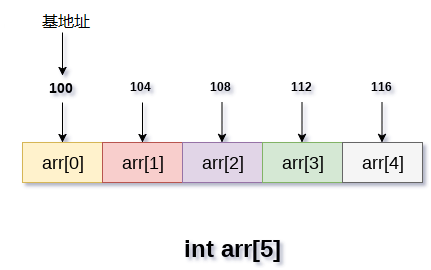
数组1 数组的简介定义 数组是存储在连续内存位置的相同类型数据项的集合，是最简单的线性数据结构。 数组的每个数据元素都可以使用下表索引运算符，进行随机访问。 数组可以有一个或多个维度。 每个元素具有相同的数据类型并且具有相同的大小，即int = 4个字节。 123int arr[10];char arr[10]; float arr[5]; 优点 数组为同一类型的变量组提供单一名称，因此很容易记住数组中所有元素的名称。 遍历数组是一个非常简单的过程，只需要递增数组的基址，就可以逐个访问每个元素。 可以使用索引直接访问数组中的任何元素。 时间复杂性 算法 平均情况 最坏情况 访问 O(1) O(1) 搜索 O(n) O(n) 插入 O(n) O(n) 删除 O(n) O(n) 空间复杂性 在数组中，最坏情况下的空间复杂度是O(n)。 2 数组的类型一维数组 一维（或单维）数组是一种线性数组，其中元素的访问是以行或列索引的单一下标表示。 C++ 将高维维数组存储为一维数组。因此，如果我们将 A 定义为也包含 M * N 个元素的二维数...

链表1 简介链表概念 链表是一种随机存储在内存中的节点对象集合。 节点包含两个字段，即存储在该地址的数据和包含下一个节点地址的指针。 链表的最后一个节点包含指向null的指针。 链表特点 链表不需要连续存在于存储器中。节点可以是存储器中的任何位置并链接在一起以形成链表。这实现了空间的优化利用。 链表大小仅限于内存大小，不需要提前声明。 空节点不能出现在链表中。 在单链表中存储基元类型或对象的值。 链表与数组的对比 数组有以下限制： 在程序中使用数组之前，必须事先知道数组的大小。 增加数组的大小是一个耗时的过程。在运行时几乎不可能扩展数组的大小。 数组中的所有元素都需要连续存储在内存中。在数组中插入任何元素都需要移动元素之前所有的数据。 链表是可以克服数组所有限制的数据结构。 链表是非常有用的，因为， 它动态分配内存。链表的所有节点都是非连续存储在存储器中，并使用指针链接在一起。 大小调整不再是问题，因为不需要在声明时定义大小。链表根据程序的需求增长，并且仅限于可用的内存空间。 2 链表的类型分类 单链表 双链表 循环单链表 循环双链表

单链表1 简介概念 单链表是有序元素集的集合。元素的数量可以根据程序的需要而变化。 单链表中的节点由两部分组成：数据部分和链接部分。 节点的数据部分存储将由节点表示的实际信息，而节点的链接部分存储其直接后继的地址。 单向链或单链表可以仅在一个方向上遍历。也就是说每个节点只包含下一个节点的指针，因此不能反向遍历链表。 链表复杂度 操作 平均复杂度 最坏复杂度 访问 θ(n) θ(n) 搜索 θ(n) θ(n) 插入 θ(1) θ(1) 删除 θ(1) θ(1) 2 链表的存储和实现链表的存储 链表不需要连续存在于存储器中。节点可以是存储器中的任何位置并链接在一起以形成链表。这实现了空间的优化利用。 链表的实现 链表通过结构体和指针实现 1234567struct node { int data; struct node *next; }; struct node *head, *ptr; ptr = (struct node *)malloc(sizeof(struct node *)); ...

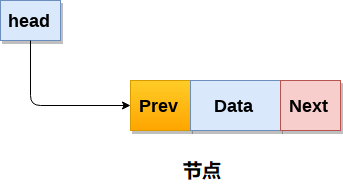
双链表1 双链表的简介概念 双向链表是一种复杂类型的链表，它的节点包含指向序列中前一个节点和下一个节点的指针。 在双向链表中，节点由三部分组成：节点数据，指向下一个节点的指针(next指针)，指向前一个节点的指针(prev指针)。 2 双链表的存储和实现数据存储 双向链表为每个节点消耗更多空间 可以更灵活地操作链表中的元素。 数据实现 使用结构体和指针实现。 123456struct node { struct node *prev; int data; struct node *next; } 使用STL中的list实现 12#include<list>list<int> li; 3 双链表的操作基本操作 创建 遍历、搜索 插入 删除 实现12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656...

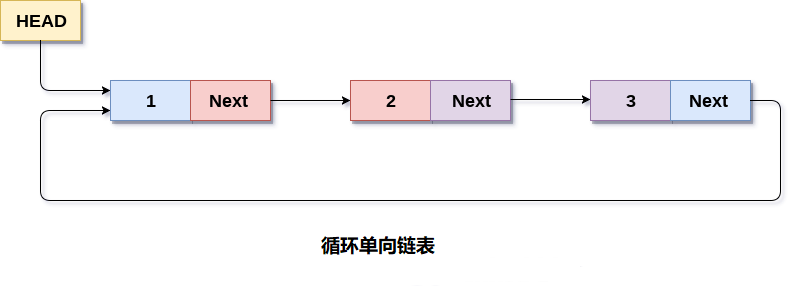
循环单向链表1 简介概念 在循环单链表中，链表的最后一个节点包含指向链表的第一个节点的指针。可以有循环单向链表以及循环双链表。 遍历一个循环单链表，直到到达开始的同一个节点。循环单链表类似于链表，但它没有开始也没有结束。任何节点的下一部分都不存在NULL值。 2 数据存储和实现数据存储链表的最后一个节点包含链表的第一个节点的地址。 数据实现 链表通过结构体和指针实现 1234567struct node { int data; struct node *next; }; struct node *head, *ptr; ptr = (struct node *)malloc(sizeof(struct node *)); C++ STL提供了链表的实现 1234#include<list>list<int> li;forward_list<int> li; 3 操作基本操作 创建 遍历、搜索 插入 删除 实现1234567891011121314151617181920212...

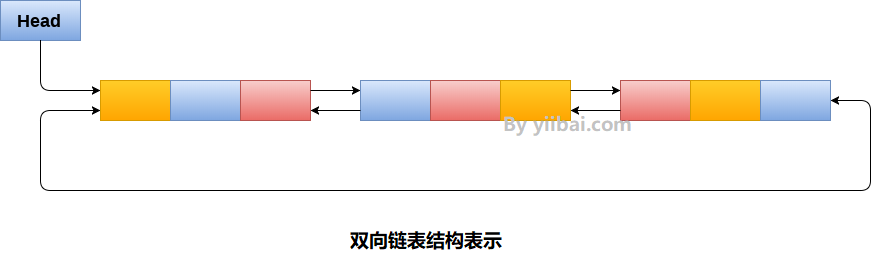
循环双向链表1 简介概念 循环双向链表是一种更复杂的数据结构类型，它的节点包含指向其前一节点以及下一节点的指针。 循环双向链表在任何节点中都不包含NULL。 链表的最后一个节点包含列表的第一个节点的地址。 链表的第一个节点还包含的前一个指针是指向最后一个节点的地址。 2 数据存储和实现数据存储 起始节点包含最后一个(也是前一个)节点的地址，即8和下一个节点，即4。链表的最后一个节点，存储在地址8并包含数据6，包含链表的第一个节点的地址 数据实现 使用结构体和指针实现。 123456struct node { struct node *prev; int data; struct node *next; } 使用STL中的list实现 12#include<list>list<int> li; 3 操作基本操作 创建 遍历、搜索 插入 删除 实现1234567891011121314151617181920212223242526272829303132333435363738394...

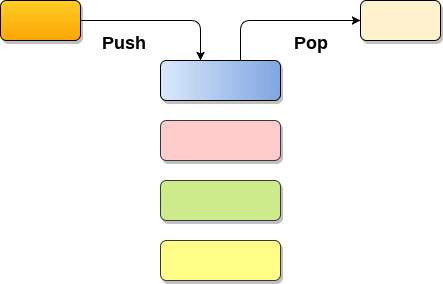
堆栈1 简介概念 堆栈（stack）又称为栈，是计算机科学中一种特殊的串列形式的抽象数据类型， 堆栈(Stack)是一个有序列表，它只能在顶端执行插入和删除。 堆栈(Stack)是一个递归数据结构，具有指向其顶部元素的指针。 堆栈为后进先出(LIFO)列表，即首先插入堆栈的元素将最后从堆栈中删除. 应用 深度优先搜索与回溯 递归 表达式评估和转换 解析 浏览器 编辑器 树遍历 特点 先入后出，后入先出。 除头尾节点之外，每个元素有一个前驱，一个后继。 2 栈的操作基础操作 推入 push 将数据放入堆栈的顶端（数组形式或串列形式），堆栈顶端 top 指针加一。 弹出 pop 将顶端数据数据输出（回传），堆栈顶端数据减一。 查看 top 查看栈顶的元素而不删除它们。 以后有时间来实现这些数据结构 3 栈的实现数组实现12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656...

单调栈定义 单调栈中存放的数据应该是有序的，所以单调栈也分为单调递增栈和单调递减栈 单调递增栈：单调递增栈就是从栈底到栈顶数据是从小到大 单调递减栈：单调递减栈就是从栈底到栈顶数据是从大到小 规则 （单调递减栈）现在有一组数10，3，7，4，12。从左到右依次入栈，则如果栈为空或入栈元素值小于栈顶元素值，则入栈；否则，如果入栈则会破坏栈的单调性，则需要把比入栈元素小的元素全部出栈。 0入栈时，栈为空，直接入栈，栈内元素为10。 入栈时，栈顶元素10比3大，则入栈，栈内元素为10，3。 入栈时，栈顶元素3比7小，则栈顶元素出栈，此时栈顶元素为10，比7大，则7入栈，栈内元素为10，7。 入栈时，栈顶元素7比4大，则入栈，栈内元素为10，7，4。 2入栈时，栈顶元素4比12小，4出栈，此时栈顶元素为7，仍比12小，栈顶元素7继续出栈，此时栈顶元素为10，仍比12小，10出栈，此时栈为空，12入栈，栈内元素为12。 应用 局部顺序问题，可以使用单调栈解决。例如存在一个局部增序的序列。需要找到所有的局部增序的序列。则单调增栈的每次连续入栈，都是增序。每次连续出栈都是违反增序规...

队列1 简介概念 队列可以定义为有序列表。在一端执行插入操作rear，删除操作在另一端执行，称为front。 队列被称为先进先出列表。 应用 单个共享资源(如打印机，磁盘，CPU)的等待列表。 异步数据传输。管道，文件IO，套接字。 缓冲区. 操作系统中处理中断。 时间复杂度 时间复杂性 访问 搜索 插入 删除 平均情况 θ(n) θ(n) θ(1) θ(1) 最坏情况 θ(n) θ(n) θ(1) θ(1) 2 队列的操作基本操作 创建 遍历（显示第一个元素） 插入 删除 3 队列的实现队列的数组实现123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103#include<stdio.h> #in...