数据结构
文章
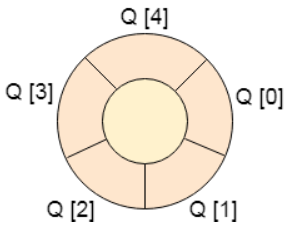
4.1 循环队列
循环队列1 简介概念 在循环队列中,最后一个索引紧跟在第一个索引之后。 当front = -1和rear = max-1时,循环队列将满。循环队列的实现类似于线性队列的实现。只有在插入和删除的情况下实现的逻辑部分与线性队列中的逻辑部分不同。 时间复杂度 操作 Front O(1) Rear O(1) enQueue() O(1) deQueue() O(1) 2 循环队列的操作基本操作 创建 遍历、搜索、查找(显示第一个元素) 插入 删除 3 循环队列的实现数组实现123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106#include<stdio.h> ...
4.2 优先队列
优先队列1 优先队列简介3 优先队列的操作基本操作 创建 遍历、搜索、查找(显示第一个元素) 插入 删除 3 优先队列的实现数组实现循环链表实现C++模板123#include<queue>queue<int> que;
5 散列表
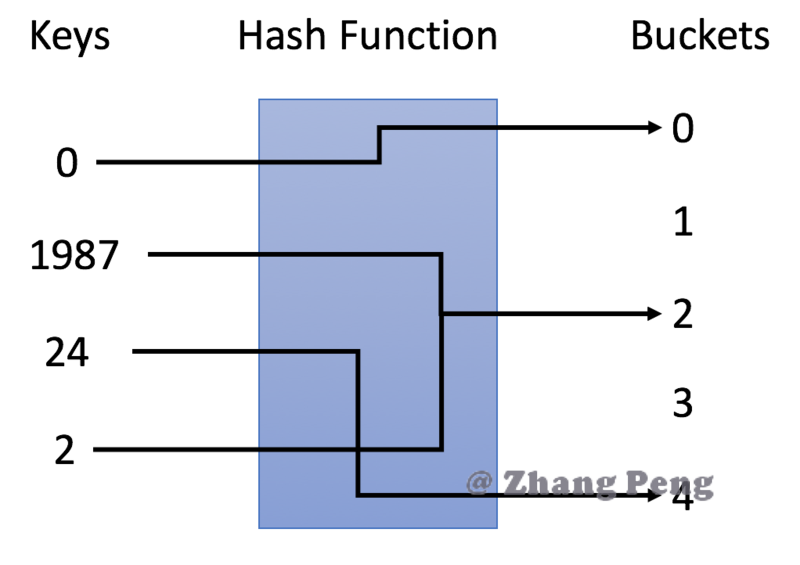
哈希表 包含集合和映射。即unordered_set和unordreed_map两种数据结构的实现方式。 参考文献 https://www.cnblogs.com/gongcheng-/p/10894205.html#_label1_0 1 哈希表简介哈希表的概念 哈希表是一种使用哈希函数组织数据,以支持快速插入和搜索的数据结构。 通过选择合适的哈希函数,哈希表可以在插入和搜索方面实现出色的性能。 哈希表的分类 有两种不同类型的哈希表:哈希集合和哈希映射。 哈希集合是集合set数据结构的实现之一,用于存储非重复值。 哈希映射是映射map 数据结构的实现之一,用于存储(key, value)键值对。 2 哈希表的原理原理说明 哈希表的关键思想是使用哈希函数将键映射到存储桶。更确切地说, 当我们插入一个新的键时,哈希函数将决定该键应该分配到哪个桶中,并将该键存储在相应的桶中; 当我们想要搜索一个键时,哈希表将使用相同的哈希函数来查找对应的桶,并只在特定的桶中进行搜索。 哈希函数 在示例中,我们使用 y = x % 5 作为哈希函数。让我们使用这个例...
5.1 散列表查找
Hash 表的查找要点哈希表和哈希函数在记录的存储位置和它的关键字之间是建立一个确定的对应关系(映射函数),使每个关键字和一个存储位置能唯一对应。这个映射函数称为哈希函数,根据这个原则建立的表称为哈希表(Hash Table),也叫散列表。 以上描述,如果通过数学形式来描述就是: 若查找关键字为 key,则其值存放在 f(key) 的存储位置上。由此,不需比较便可直接取得所查记录。 注:哈希查找与线性表查找和树表查找最大的区别在于,不用数值比较。 冲突若 key1 ≠ key2 ,而 f(key1) = f(key2),这种情况称为冲突(Collision)。 根据哈希函数f(key)和处理冲突的方法将一组关键字映射到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这一映射过程称为构造哈希表。 构造哈希表这个场景就像汽车找停车位,如果车位被人占了,只能找空的地方停。 构造哈希表由以上内容可知,哈希查找本身其实不费吹灰之力,问题的关键在于如何构造哈希表和处理冲突。 常见的构造哈希表的方法有 5 种: 直接定址法说白了,就是小学时学...
5.4 并查集
并查集 参考文献 https://zhuanlan.zhihu.com/p/93647900/ https://blog.csdn.net/qq_41754350/article/details/81271567 1 概念定义并查集被很多OIer认为是最简洁而优雅的数据结构之一,主要用于解决一些元素分组的问题。它管理一系列不相交的集合,并支持两种操作: 合并(Union):把两个不相交的集合合并为一个集合。 查询(Find):查询两个元素是否在同一个集合中。 2 并查集原理初始化 初始化所有的节点的根节点是自己。 假如有编号为1, 2, 3, …, n的n个元素,我们用一个数组fa[]来存储每个元素的父节点(因为每个元素有且只有一个父节点,所以这是可行的)。一开始,我们先将它们的父节点设为自己。 查询 我们用递归的写法实现对代表元素的查询:一层一层访问父节点,直至根节点(根节点的标志就是父节点是本身)。要判断两个元素是否属于同一个集合,只需要看它们的根节点是否相同即可。 合并 合并操作也是很简单的,先找到两个集合的代表元素,然后将前者的...
6 树
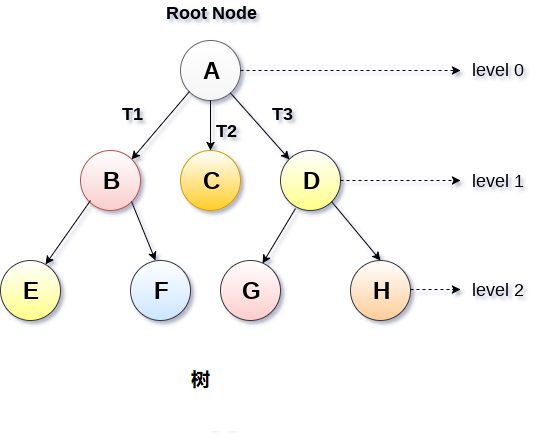
树 树 0 简介定义树是一种抽象数据类型或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由 n(n>0)个有限节点组成一个具有层次关系的集合。 树是一种递归数据结构,包含一个或多个数据节点的集合,其中一个节点被指定为树的根,而其余节点被称为根的子节点。 除根节点之外的节点被划分为非空集,其中每个节点将被称为子树。 树的节点要么保持它们之间的父子关系,要么它们是姐妹节点。 在通用树中,一个节点可以具有任意数量的子节点,但它只能有一个父节点。 特点 每个节点都只有有限个子节点或无子节点。 树有且仅有一个根节点。 根节点没有父节点;非根节点有且仅有一个父节点。 每个非根节点可以分为多个不相交的子树。 树里面没有环路。 术语 祖先节点: 节点的祖先是从根到该节点的路径上的任何前节点。根节点没有祖先节点。 父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 子节点:一个节点含有的子树的根节点称为该节点的子节点; 根节点: 根节点是树层次结构中的最顶层节点。 换句话说,根节点是没有任何父节点的节点. 叶子节点或终端节点:度为零的...
6.1 二叉树
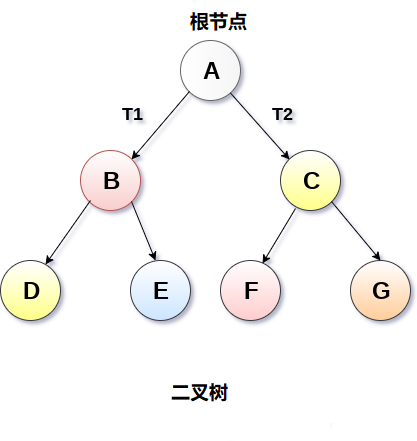
二叉树 树>二叉树 1 二叉树简介概念 二叉树是一种特殊类型的通用树,它的每个节点最多可以有两个子节点。 二叉树通常被划分为三个不相交的子集。 节点的根 左二叉树 右二叉树 性质 二叉树第 i 层上的结点数目最多为 2i-1 (i≥1)。 深度为 k 的二叉树至多有 2k-1 个结点(k≥1)。 包含 n 个结点的二叉树的高度至少为 log2(n+1)。 在任意一棵二叉树中,若终端结点的个数为 n0,度为 2 的结点数为 n2,则 n0=n2+1。 2 二叉树分类严格二叉树 在严格二叉树中,每个非叶节点包含非空的左和右子树。 换句话说,每个非叶节点的等级将始终为2。具有n个叶子的严格二叉树将具有(2n-1)个节点。 完全二叉树 如果所有叶子都位于相同的水平d,则称二元树是完全二叉树。完全二叉树是二叉树,在0级和d级之间的每个级别包含正好$2^d$个节点。 具有深度d的完全二叉树中的节点总数是$2^{(d+1)}-1$,其中叶节点是$2^d$,非叶节点是$2^d-1$。 3 二叉树的操作——遍历搜索遍历搜索方法 深度优先搜索(DFS) 在这个策...
6.2 二叉搜索树
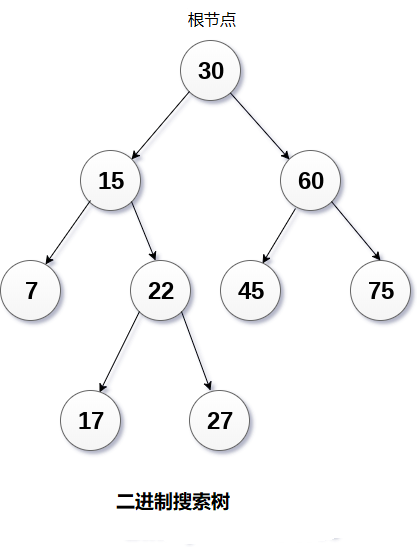
二叉搜索树 树>二叉树>二叉搜索树 1 简介概念 二叉搜索树是二叉树,其节点按特定顺序排列。也称为称为有序二叉树。 左子树中所有节点的值小于根的值。 右子树中所有节点的值大于或等于根的值。 此规则将递归地应用于根的所有左子树和右子树 优点 在搜索过程中,它会在每一步删除半个子树。 在二叉搜索树中搜索元素需要o(log2n)时间。 在最坏的情况下,搜索元素所花费的时间是0(n)。 与数组和链表中的操作相比,它还加快了插入和删除操作。 2 基本操作基本操作 创建 遍历(同上) 插入 删除 遍历 二叉搜索树的前序遍历。 二叉搜索书的中序遍历。中序的输出结果其实就是二叉搜索树排序后的结果。 二叉搜索树的后续遍历。 插入 使用下列元素创建二叉树的过程 143, 10, 79, 90, 12, 54, 11, 9, 50 删除3 二叉搜索树实现1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859...