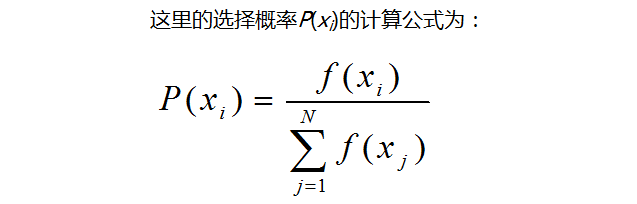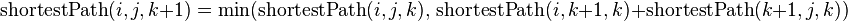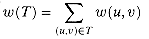补充
文章
单源最短路问题
单元最短路问题 通过不同的方式解决单元最短路问题 图,不是树 0 问题描述单元最短路问题、有向无环图 1 暴力求解深度优先搜索DFS广度优先搜索BFS2 回溯法深度优先算法,每次回溯的时候进行剪枝操作。如果此分支没有希望比已经保存的最短路更优。 而且可以从不同的点到达同一个点。保留之前到达这个点的状态,如果最新到达这个点的距离小于之前的距离,则继续向下走,如果大于则放弃并回溯。
遗传算法详解
遗传算法定义 遗传算法(Genetic Algorithm,GA)起源于对生物系统所进行的计算机模拟研究。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法,借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法,能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应地控制搜索过程以求得最佳解。 袋鼠跳问题(纯粹是觉得有意思) “袋鼠跳”问题 既然我们把函数曲线理解成一个一个山峰和山谷组成的山脉。那么我们可以设想所得到的每一个解就是一只袋鼠,我们希望它们不断的向着更高处跳去,直到跳到最高的山峰(尽管袋鼠本身不见得愿意那么做)。所以求最大值的过程就转化成一个“袋鼠跳”的过程。 作为对比下面简单介绍“袋鼠跳”的几种方式。 1. 爬山法(最速上升爬山法): 从搜索空间中随机产生邻近的点,从中选择对应解最优的个体,替换原来的个体,不断重复上述过程。因为爬山法只对“邻近”的点作比较,所以目光比较“短浅”,常常只能收敛到离开初始位置比较近的局部最优解上面。对于存在很多局部最优点的问题,通过一个简单的迭代找出全局最优解的机会非常渺茫。(在爬山法中,袋鼠最有希望...
Bellman-Ford 单源最短路径算法
Bellman-Ford 单源最短路径算法 Bellman-Ford 算法是一种用于计算带权有向图中单源最短路径(SSSP:Single-SourceShortest Path)的算法。该算法由 Richard Bellman 和 Lester Ford 分别发表于 1958年和 1956 年,而实际上 Edward F. Moore 也在 1957年发布了相同的算法,因此,此算法也常被称为 Bellman-Ford-Moore 算法。 Bellman-Ford 算法和 Dijkstra算法同为解决单源最短路径的算法。对于带权有向图G = (V, E),Dijkstra 算法要求图 G 中边的权值均为非负,而 Bellman-Ford算法能适应一般的情况(即存在负权边的情况)。一个实现的很好的Dijkstra 算法比 Bellman-Ford 算法的运行时间要低。 Bellman-Ford 算法采用动态规划(Dynamic Programming)进行设计,实现的时间复杂度为O(V*E),其中 V 为顶点数量,E 为边的数量。Dijkstra 算法采用贪心算法(Gree...
Dijkstra 单源最短路径算法
Dijkstra 单源最短路径算法 Dijkstra 算法是一种用于计算带权有向图中单源最短路径(SSSP:Single-SourceShortest Path)的算法,由计算机科学家 Edsger Dijkstra 于 1956 年构思并于 1959年发表。其解决的问题是:给定图 G 和源顶点 v,找到从 v 至图中所有顶点的最短路径。 Dijkstra 算法采用贪心算法(GreedyAlgorithm)范式进行设计。在最短路径问题中,对于带权有向图 G = (V, E),Dijkstra算法的初始实现版本未使用最小优先队列实现,其时间复杂度为 O(V2),基于 Fibonacciheap的最小优先队列实现版本,其时间复杂度为 O(E + VlogV)。 Bellman-Ford算法和Dijkstra算法同为解决单源最短路径的算法。对于带权有向图G = (V, E),Dijkstra 算法要求图 G 中边的权值均为非负,而 Bellman-Ford算法能适应一般的情况(即存在负权边的情况)。一个实现的很好的 Dijkstra 算法比Bellman-For...
Floyd-Warshall 全源最短路径算法
Floyd-Warshall 全源最短路径算法 Floyd-Warshall 算法采用动态规划方案来解决在一个有向图 G = (V, E)上每对顶点间的最短路径问题,即全源最短路径问题(All-Pairs Shortest PathsProblem),其中图 G 允许存在权值为负的边,但不存在权值为负的回路。Floyd-Warshall算法的运行时间为 Θ(V3)。 Floyd-Warshall 算法由 Robert Floyd 于 1962 年提出,但其实质上与 Bernad Roy 于1959 年和 Stephen Warshall 于 1962 年提出的算法相同。 解决单源最短路径问题的方案有 Dijkstra算法和Bellman-Ford算法,对于全源最短路径问题可以认为是单源最短路径问题(SingleSource Shortest PathsProblem)的推广,即分别以每个顶点作为源顶点并求其至其它顶点的最短距离。更通用的全源最短路径算法包括: 针对稠密图的 Floyd-Warshall 算法:时间复杂度为 O(V3); 针对稀疏图的 Johnson ...
Kruskal 最小生成树算法
Kruskal 最小生成树算法 对于一个给定的连通的无向图 G = (V, E),希望找到一个无回路的子集 T,T 是 E的子集,它连接了所有的顶点,且其权值之和为最小。 因为 T 无回路且连接所有的顶点,所以它必然是一棵树,称为生成树(SpanningTree),因为它生成了图 G。显然,由于树 T 连接了所有的顶点,所以树 T 有 V - 1条边。一张图 G 可以有很多棵生成树,而把确定权值最小的树 T的问题称为最小生成树问题(Minimum Spanning Tree)。术语 “最小生成树”实际上是 “最小权值生成树” 的缩写。 Kruskal 算法提供一种在 O(ElogV) 运行时间确定最小生成树的方案。Kruskal算法基于贪心算法(GreedyAlgorithm)的思想进行设计,其选择的贪心策略就是,每次都选择权重最小的但未形成环路的边加入到生成树中。其算法结构如下: 将所有的边按照权重非递减排序; 选择最小权重的边,判断是否其在当前的生成树中形成了一个环路。如果环路没有形成,则将该边加入树中,否则放弃。 重复步骤 2,直到有 V - 1 条边在生...
P问题、NP问题和NPC问题
时间复杂度 时间复杂度并不是表示一个程序解决问题需要花多少时间,而是当问题规模扩大后,程序需要的时间长度增长得有多快。也就是说,对于高速处理数据的计算机来说,处理某一个特定数据的效率不能衡量一个程序的好坏,而应该看当这个数据的规模变大到数百倍后,程序运行时间是否还是一样,或者也跟着慢了数百倍,或者变慢了数万倍。不管数据有多大,程序处理花的时间始终是那么多的,我们就说这个程序很好,具有O(1)的时间复杂度,也称常数级复杂度;数据规模变得有多大,花的时间也跟着变得有多长,这个程序的时间复杂度就是O(n),比如找n个数中的最大值;而像冒泡排序、插入排序等,数据扩大2倍,时间变慢4倍的,属于O(n^2)的复杂度。还有一些穷举类的算法,所需时间长度成几何阶数上涨,这就是O(a^n)的指数级复杂度,甚至O(n!)的阶乘级复杂度。不会存在O(2*n^2)的复杂度,因为前面的那个“2”是系数,根本不会影响到整个程序的时间增长。同样地,O(n^3+n^2)的复杂度也就是O(n^3)的复杂度。因此,我们会说,一个O(0.01*n^3)的程序的效率比O(100*n^2)的效率低,尽管在n很小的时候,前...
Prim 最小生成树算法
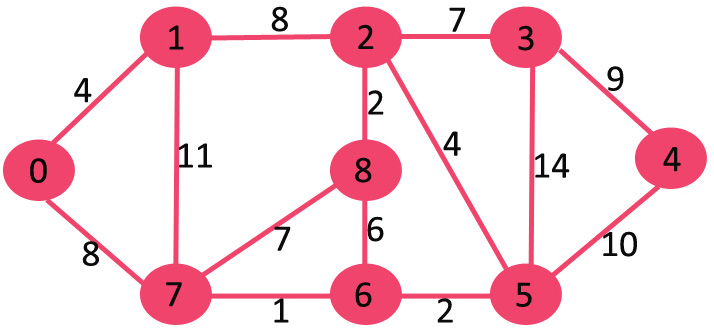
Prim 最小生成树算法 Prim 算法是一种解决**最小生成树问题(Minimum Spanning Tree)**的算法。和Kruskal算法类似,Prim算法的设计也是基于贪心算法(Greedy algorithm)。 Prim算法的思想很简单,一棵生成树必须连接所有的顶点,而要保持最小权重则每次选择邻接的边时要选择较小权重的边。Prim算法看起来非常类似于单源最短路径 Dijkstra算法,从源点出发,寻找当前的最短路径,每次比较当前可达邻接顶点中最小的一个边加入到生成树中。 例如,下面这张连通的无向图 G,包含 9 个顶点和 14条边,所以期待的最小生成树应包含 (9 - 1) = 8 条边。 创建 mstSet 包含到所有顶点的距离,初始为 INF,源点 0 的距离为 0,{0, INF, INF,INF, INF, INF, INF, INF, INF}。 选择当前最短距离的顶点,即还是顶点 0,将 0 加入 MST,此时邻接顶点为 1 和 7。 选择当前最小距离的顶点 1,将 1 加入 MST,此时邻接顶点为 2。 选择 2 和 7 中最小距离的顶...
TSP旅行商问题
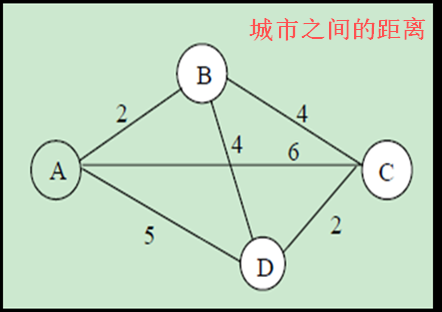
问题分析 有若干个城市,任何两个城市之间的距离都是确定的,现要求一旅行商从某城市出发必须经过每一个城市且只在一个城市逗留一次,最后回到出发的城市,问如何事先确定一条最短的线路已保证其旅行的费用最少? 贪心算法 动态规划算法 分支限界算法 遗传算法