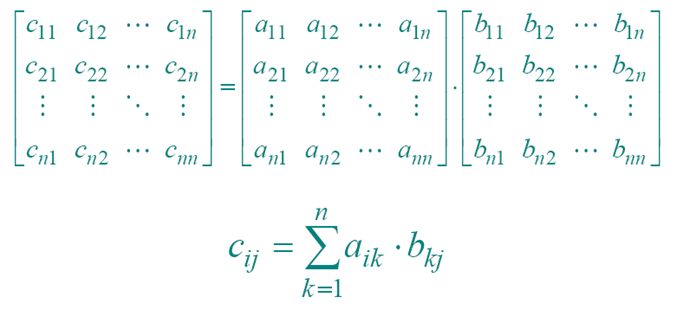Estom的博客

等到以后再处理。

主要是利用位运算解决一些巧妙的问题。 1 基础位运算基础 符号 说明 特性 & 按位与 只要有0，返回0 | 按位或 只要有1，返回1 ^ 按位异或 相同返回0。不同返回1 ~ 按位取反 全部反转。不重复的数字 >> 右移 << 左移 负数在计算机中使用补码表示，主要目标就是实现了最小值到最大值之间，位运算的连续性。 在字面数字运算中，-2 加1为-1，-1 加1为0，0+1为1。是连续计算的。在二级制补码计算中。也满足上述的计算规则。1111表示-1，加一通过溢出一位，变为0000，成为0. 实际上-1是按位绝对值最大的数，即1111。 特殊性质 操作 性质 n & (n - 1) n中的最后一个1变成0。 n & (~n + 1) n&(n^(n-1)) lowbit()运算，n中最后一个1保留。 (~n) + 1== -n 计算机中补码表示的-n。位运算取反 n/2 等价于 右移一位 n >> 1 n*2 等价...

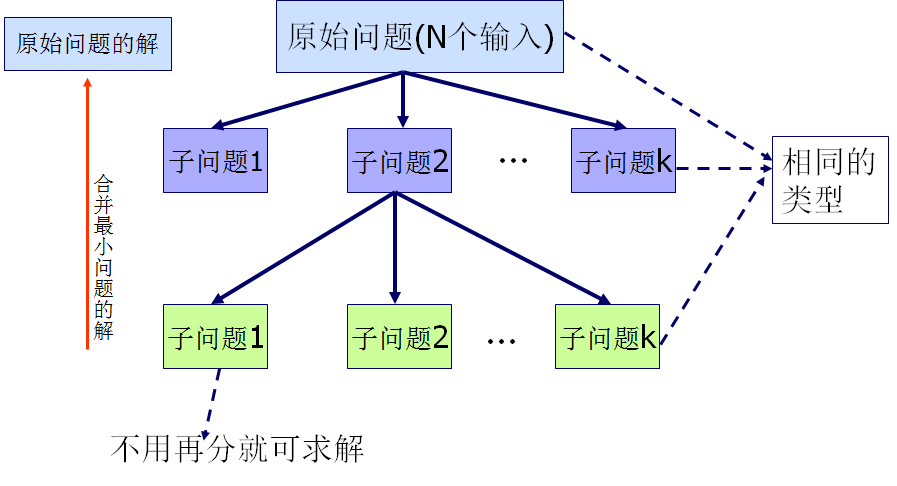
分治法1 分治法概述基本思想 求解问题算法的复杂性一般都与问题规模相关，问题规模越小越容易处理。 分治法的基本思想是，将一个难以直接解决的大问题，分解为规模较小的相同类型的子问题，直至这些子问题容易直接求解，并且可以利用这些子问题的解求出原问题的解。各个击破，分而治之。 分治法产生的子问题一般是原问题的较小模式，这就为使用递归技术提供了方便。递归是分治法中最常用的技术。 分治法解决问题的先决条件 该问题的规模缩小到一定的程度就可以容易地解决； 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质； 利用该问题分解出的子问题的解可以合并为该问题的解； 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。 分治法的步骤一般来说，分治法的求解过程由以下三个阶段组成： 划分divede：既然是分治，当然需要把规模为n的原问题划分为k个规模较小的子问题，并尽量使这k个子问题的规模大致相同。 解决conquer：各子问题的解法与原问题的解法通常是相同的，可以用递归的方法求解各个子问题，有时递归处理也可以用循环来实现。 合并merge：把各个子问题的...

排列问题1 排列问题-分治法、递归法问题描述R是由n个元素构成的序列集合，R={r1, r2, … ,rn}，求R的全排列perm(R)。 问题分析 若R中只有1个元素{r}，则perm(R)=(r) 若R中只有2个元素{r1, r2}，则 perm(R)=(r1)perm(R1)∪(r2)perm(R2) 其中，Ri=R-{ri} 若R中有3个元素{ r1, r2, r3}，则 perm(R)=(r1)perm(R1)∪(r2)perm(R2)∪(r3)perm(R3) 策略选择 算法思想：分治法 算法设计 划分：依次将待排列的数组的后n-1个元素与第一个元素交换。 解决：则每次递归处理的都是后n-1个元素的全排列。 合并：当数组元素仅有一个时为此递归算法的出口。即开始合并。 123456789101112算法 perm(Type list[], int k, int m)//生成列表list的全排列//输入：一个全排列元素列表list[0..n-1]//输出：list的全排列集合if k == m for i←...

大整数乘法 参考文献 大数乘法的问题及其高效的算法 问题描述 题目描述： 输出两个不超过100位的大整数的乘积。 输入： 输入两个大整数，如1234567 和 123 输出： 输出乘积，如：151851741 数字以字符串的形式给出。 1求 1234567891011121314151617181920 * 2019181716151413121110987654321 的乘积结果 问题分析 所谓大数相乘（Multiplication algorithm），就是指数字比较大，相乘的结果超出了基本类型的表示范围，所以这样的数不能够直接做乘法运算。参考了很多资料，包括维基百科词条Multiplication algorithm，才知道目前大数乘法算法主要有以下几种思路： 模拟小学乘法：最简单的乘法竖式手算的累加型； 分治乘法：最简单的是Karatsuba乘法，一般化以后有Toom-Cook乘法； 快速傅里叶变换FFT：（为了避免精度问题，可以改用快速数论变换FNTT），时间复杂度O(N lgN lglgN)。具体可参照Schönhage–Strassen algorith...

矩阵乘法1 矩阵乘法-蛮力法问题描述 问题分析算法设计问题归结为计算元素C[i,j]。依据定义来计算A和B的乘积矩阵C，则每计算C的一个元素C[i][j]，需要做n次乘法和n-1次加法。C的规模为n*n。 算法分析 时间复杂度O(n^3) 算法实现2 矩阵乘法-STRASSEN算法算法设计算法的基本思想在于以增加加减法的次数来减少乘法次数：用了7次n/2 x n/2 矩阵乘法和18次n/2 x n/2 矩阵的加法 算法过程 将矩阵分块 1234A = a11 a12 a21 a22 B = b11 b12 b21 b22 计算分块矩阵的乘法 1234567d1 = (a11 + a22) (b11 + b22)d2 = (a21 + a22) b11d3 = a11 (b12 – b22)d4 = a22 (b21 –b11)d5 = (a11 + a12) b22d6 = (a21 – a11) (b11 + b12)d7 = (a12 – a22) ( b21 + b22) 将分块矩阵乘法进...

拓扑排序-减治法问题描述考虑五门必修课的一个集合{C1, C2, C3, C4, C5},一个在职的学生必须在某个阶段修完这几门课程。可以按照任何次序学习这些课程，只要满足下面这些条件： C1和C2没有任何先决条件； 修完C1 和C2才能修C3； 修完C3 才能修C4； 修完C3、C4才能修C5； 这个学生每个学期只能修一门课程。 若用一个图来建模，它的顶点代表课程，有向边表示先决条件，该问题为：是否可以按照这种次序列出它的顶点，使得对于图中每一条边来说，边的起始顶点总是排在边的结束顶点之前。 这个问题称为拓扑排序。 如果有向图具有一个有向的回路，该问题是无解的。因此，为了使得拓扑排序成为可能，问题中的图必须是一个无环有向图。 拓扑排序-减治原理基于减（减一）治技术的一个直接实现：重复以下过程： 在余下的有向图中求出一个源，它是一个没有输入边的顶点； 然后把该源和所有从它出发的边都删除。（如果有多个这样的源，可以任意选择一个；如果这样的源不存在，算法停止，因为该问题是无解的） 顶点被删除的次序就是拓扑排序的一个解。 1234567891011121314151617181...

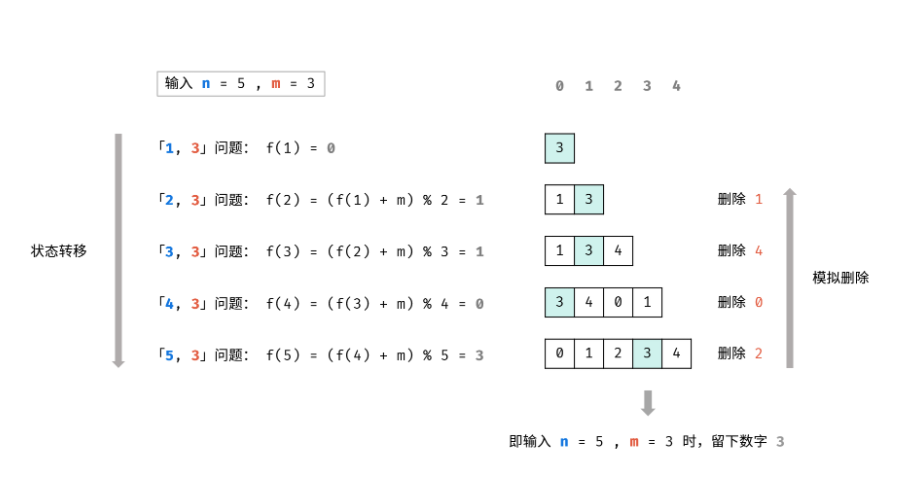
约瑟夫问题问题描述一堆人围城环。每次淘汰第m个人。最终剩下谁。 问题分析算法设计我们将上述问题建模为函数 f(n, m)，该函数的返回值为最终留下的元素的序号。 首先，长度为 n 的序列会先删除第 m % n 个元素，然后剩下一个长度为 n - 1 的序列。那么，我们可以递归地求解 f(n - 1, m)，就可以知道对于剩下的 n - 1 个元素，最终会留下第几个元素，我们设答案为 x = f(n - 1, m)。 由于我们删除了第 m % n 个元素，将序列的长度变为 n - 1。当我们知道了 f(n - 1, m) 对应的答案 x 之后，我们也就可以知道，长度为 n 的序列最后一个删除的元素，应当是从 m % n 开始数的第 x 个元素。因此有 f(n, m) = (m % n + x) % n = (m + x) % n。 算法分析算法实现 递归 12345678910111213class Solution { int f(int n, int m) { if (n == 1) { ...

元素唯一性1 元素唯一性-暴力法问题描述检验数组中元素的惟一性 算法原理暴力法 1234567UniqueElements(A[1,…n])//输出：如果A之元素全部惟一，返回“true”, 否则返回 “false”for i←1 to n-1 do for j← i+1 to n do if A[i]=A[j] return falsereturn true 算法效率n(n-1)/2 2 元素唯一性-预排序算法原理123456789PresortElementUniqueness(A[1..n])//先对数组排序来解元素惟一性问题//输入：n个可排序元素构成的一个数组A[1..n]//输出：如果A没有相等的元素，返回“true”, 否则返回”false”对数组A排序for i← 1 to n-1 do if A[i] = A[i+1] return falsereturn true 算法效率T(n)=Tsort(n) + Tscan(n) ∈Θ (nlogn) +Θ (n) = Θ (nlogn)

1 数组中的逆序对问题描述在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。 问题分析策略选择 数据结构：线性数组 算法思想：变治法。将搜索查找问题修改为排序问题。归并排序 算法设计 归并排序」是分治思想的典型应用，它包含这样三个步骤： 分解： 待排序的区间为 [l, r]，令 $m = \lfloor \frac{l + r}{2} \rfloor$，我们把 [l, r] 分成 [l,m] 和 [m+1,r] 解决： 使用归并排序递归地排序两个子序列 合并： 把两个已经排好序的子序列 [l, m][l,m] 和 [m + 1, r][m+1,r] 合并起来 在归并排序过程中。后边列表的数添加到前边之后。前边列表中数的量，就是本次排序逆序数的量。 算法分析 时间复杂度：同归并排序 O(nlogn)。 空间复杂度：同归并排序 O(n)， 算法实现12345678910111213141516171819202122232425262728293031323334353637383940...