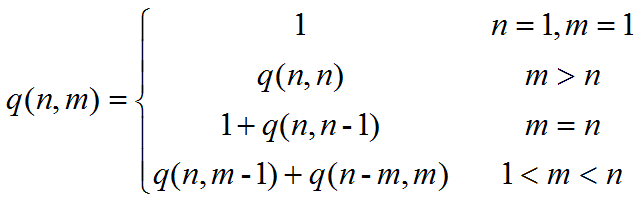Estom的博客

最近对问题1 最近对问题 暴力求解问题描述 给定平面上n个点。找其中的一对点。使得在n个点组成的所有点对中，该点对之间的距离最小。 问题分析 找出一个包含n个点的集合中距离最近的两个点。 题直观的解决方法便是Brute Force(暴力求解)。时间复杂度为O（n^2） 选择策略 分别计算每一点对之间的距离，然后从中找出距离最小的那一对。为了避免同一点对计算两次，可以只考虑i<j的点对(Pi, Pj) 算法设计 算法 bruteForceClosesPoints(P) 12345678910//蛮力法求解平面中距离最近的两点//输入：一个n(n≥2)个点的列表P，P1=(x1, y1)，…，Pn=(xn, yn)//输出：两个最近点的下标dmin←∞for i←0 to n-2 do for j←i+1 to n-1 do d←(xi-xj)2+(yi-yj)2 if d<dmin dmin←d; index1←i; index2←j;return index1,index2 正确性证明算法分析$O(n^2)$ 程序设计2 最近对问题...

整数划分问题描述将给定正整数n表示成一系列正整数之和n=n1+n2+…+nk，其中n1≥n2≥…≥nk≥1，k≥1。求最大加数不大于m的划分个数p(n,m)。 算法设计 算法实现12345678910111213#include<iostream>using namespace std;int q(int n,int m){ if((n<1)||(m<1)) return 0; if((n == 1)||(m == 1)) return 1; if(n < m) return q(n,n); if(n == m) return q(n,m-1)+1; return q(n,m-1)+q(n-m,m);

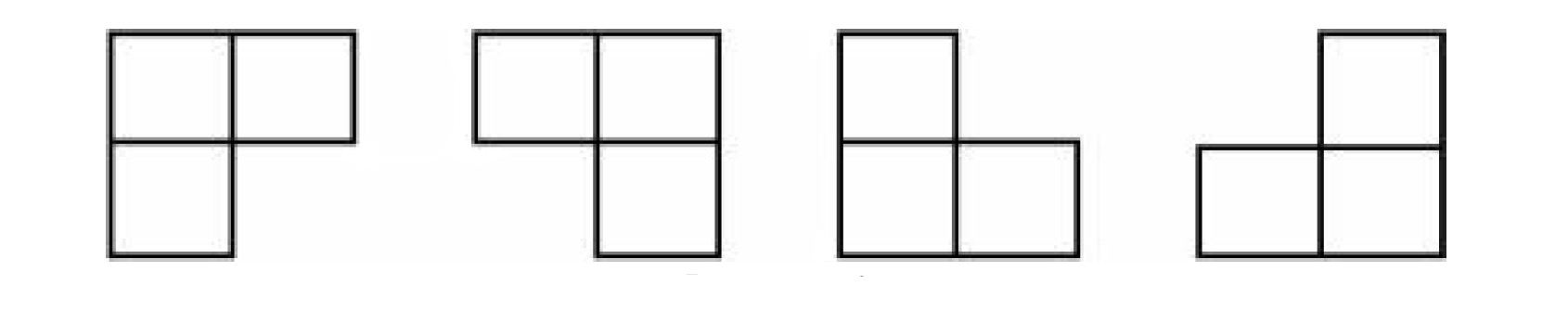
棋盘覆盖问题问题描述棋盘覆盖问题。有一个$2^k∗2^k$的方格棋盘，恰有一个方格是黑色的，其他为白色。你的任务是用包含3个方格的L型牌覆盖所有白色方格。黑色方格不能被覆盖，且任意一个白色方格不能同时被两个或更多牌覆盖。如图所示为L型牌的4种旋转方式。 求解棋盘覆盖的方法。 问题分析 问题分类： 策略选择 数据结构：线性数据结构 算法思想：分治法 算法设计分治三步骤 划分问题：将$2^k∗2^k$的棋盘划分为 $2^{k−1}∗2^{k−1}$这样的子棋盘4块。 递归求解：递归填充各个格子，填充分为四个情况，在下面会有解释，递归出口为 k=0k=0也就是子棋盘方格数为1。 合并问题：不需要合并子问题。 分治方法：将棋盘等分为四块。然后分为以下两种情况。 额外的方格在某一块中，不需要处理该区块。 额外的方格不在某一块中。则添加一个L型牌覆盖三个没有额外方格的块。 重复以上步骤直到能完全覆盖。 算法分析算法实现12345678910111213141516171819202122232425262728293031323334353637383940...

生成子集问题——迭代问题描述给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。 示例 1： 12输入：nums = [1,2,2]输出：[[],[1],[1,2],[1,2,2],[2],[2,2]] 问题分析策略选择 算法思想：迭代求解 算法设计 迭代思想，减治思想。每次选择一个元素，参与构建子集。 首先对元素去重。记录重复元素的个数。如果多个重复元素分散在其他数组中没有意义。所有多个重复元素在一起的情况下组合到之前的解集中。 这也算是一种动态规划的思想？每次都利用之前构建好的集合。构成新的解集集合。 算法分析 时间复杂度：$O(n×2^n)$ 空间复杂度：$O(n)$.结果一般不算在空间复杂度当中。 算法实现1234567891011121314151617181920212223242526272829class Solution {public: vector<vector<int>> subsetsWithDup...

最大公约数循环法1234567891011121314151617181920212223242526272829303132#include<iostream>using namespace std;int gcd1(int x,int y){ if(x%y==0){ return y; } return gcd1(y,x%y);}int gcd2(int x,int y){ int r = x % y; while( r ) { x = y; y = r; r = x % y; } return y;}int lcm(int x,int y){ int k = gcd2(x,y); return x*y/k;}int main(){ int x=60,y=95; cout<<gcd1(x,y); return 0...

动态规划 参考文献 https://zhuanlan.zhihu.com/p/144655170 https://www.cxyxiaowu.com/6781.html https://mp.weixin.qq.com/s?__biz=MzUyNjQxNjYyMg==&mid=2247486923&idx=2&sn=6c1c8aeb4db68522e67ddf8c1e933660&chksm=fa0e624acd79eb5cdb410808921609a830b9b9221e813e4eb89cf551ca48f317668d44b095d2&scene=21#wechat_redirect https://www.cxyxiaowu.com/7012.html 1 概述基本思想 多阶段决策问题。比如最短路线问题，机器负荷问题等，把解决这一类问题的的方法称为动态规划方法 动态规划算法与分治法类似，其思想把求解的问题分成许多阶段或多个子问题，然后按顺序求...

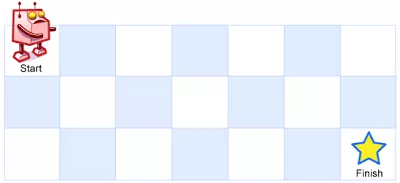
动态规划——矩阵动态规划 矩阵可以看作是图的一种，怎么说？你可以把整个矩阵当成一个图，矩阵里面的每个位置上的元素当成是图上的节点，然后每个节点的邻居就是其相邻的上下左右的位置 矩阵类动态规划的两个规模增长方向可能存在两种情况：等价独立和非等价独立。例如不同路径和最大矩形中的规模增长方向，是等价独立的，两个规模增长的含义是一样的，比较好判断。但是在背包问题等其他子问题中。规模增长的方向是不等价，一个是背包容量的增长，另一个是物品数量的增长，通常比较难发现。 在矩阵动态规划中，两个维度的增长方向是可以相互交换的。只要设计好即可。但有可能存在一个简单一个复杂的情况。 不同路径 最大矩形 1 不同路径问题描述一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。 问总共有多少条不同的路径？例如，上图是一个7 x 3 的网格。有多少可能的路径？说明： m 和 n 的值均不超过 100。 示例 1: 12345678输入: m = 3, n = 2输出:...

1 三角形数组最小路径和问题描述给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。 例如，给定三角形： 1234567[ [2], [3,4], [6,5,7], [4,1,8,3]]自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。 说明：如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。 问题分析策略选择算法设计 问题分解划分阶段：规模增长方向，从下到上（不用判断边界）。阶段n=n,n-1,…,1 确定状态变量：k阶段的状态变量是数组X[n]内的前k项，组成的状态变量集合。 状态转移方程。k阶段的状态变量X_k[n],分两种情况讨论。X_k[j]可能有两种情况，利用了上一阶段X_k-1[j]的长度。或者领了X_k-1[j+1]的长度。$$X_{k}[j]=min{X_{k-1}[j-1]+triangle[j],X_{k-1}[j+1]+triangle[j]}$$ 确定边界实现过程。初始值为0。从最后一层开始。 算法实现12345...

动态规划——线性动态规划 主要用来熟练动态规划的步骤 斐波那契数列 青蛙跳台阶 最大子段和 1 斐波那契数列问题描述 写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下： 12F(0) = 0,   F(1) = 1F(N) = F(N - 1) + F(N - 2), 其中 N > 1. 斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。 链接 问题分析问题分类 数组 动态规划+迭代 选择策略 数组 动态规划 原理： 以斐波那契数列性质f(n+1)=f(n)+f(n−1) 为转移方程。 算法设计 状态定义： 设$dp$为一维数组，其中 $dp[i]$ 的值代表 斐波那契数列第 $i$个数字 。 转移方程： $dp[i + 1] = dp[i] + dp[i - 1]$，即对应数列定义 $f(n + 1) = f(n) + f(n - ...

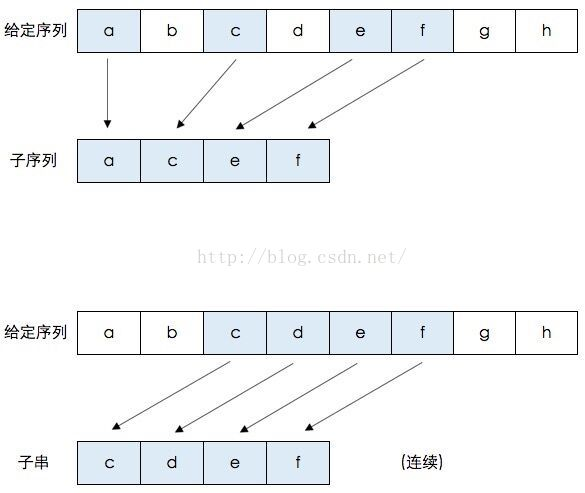
动态规划——序列动态规划 本质上也是矩阵动态规划，是特殊的矩阵动态规划，出现的频率比较高。包含两个规模增长方向，并且相互独立增长。不懂点在于题目是以序列的形式给出的。而不是矩阵形式给出的。 子序列(subsequence)： 一个特定序列的子序列就是将给定序列中零个或多个元素去掉后得到的结果(不改变元素间相对次序)。例如序列<A,B,C,B,D,A,B>的子序列有：<A,B>、<B,C,A>、<A,B,C,D,A>等。 公共子序列(common subsequence)： 给定序列X和Y，序列Z是X的子序列，也是Y的子序列，则Z是X和Y的公共子序列。例如X=[A,B,C,B,D,A,B]，Y=[B,D,C,A,B,A[，那么序列Z=[B,C,A]为X和Y的公共子序列，其长度为3。但Z不是X和Y的最长公共子序列，而序列[B,C,B,A]和[B,D,A,B]也均为X和Y的最长公共子序列，长度为4，而X和Y不存在长度大于等于5的公共子序列。对于序列[A,B,C]和序列[E,F,G]的公共子序列只有空序列[...