Estom的博客

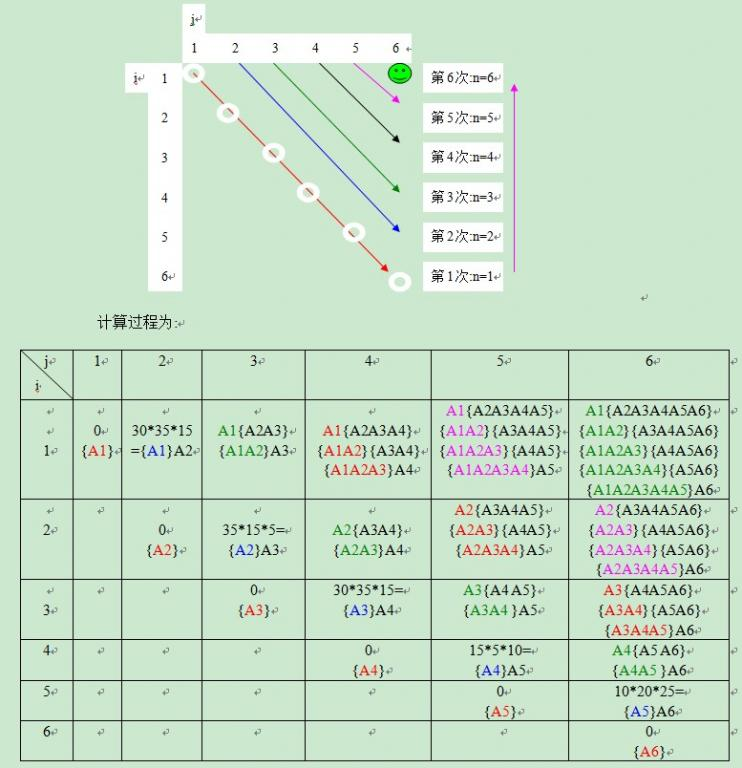
矩阵连乘问题问题描述给定n个矩阵｛A1,A2,…,An｝，其中Ai与Ai+1是可乘的，i=1，2…，n-1。如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。例如，给定三个连乘矩阵{A1，A2，A3}的维数分别是10*100，100*5和5*50，采用（A1A2）A3，乘法次数为10*100*5+10*5*50=7500次，而采用A1（A2A3），乘法次数为100*5*50+10*100*50=75000次乘法，显然，最好的次序是（A1A2)A3，乘法次数为7500次。 问题分析矩阵链乘法问题描述：给定由n个矩阵构成的序列｛A1，A2，…，An}，对乘积A1A2…An，找到最小化乘法次数的加括号方法。 策略选择 算法思想：动态规划 算法设计 问题分解划分阶段：相邻连乘的个数。相邻连乘的个数为1，的时候0次乘法。两个相邻连乘的次数固定。三个相邻连乘的时候分两次讨论。规模增长的方向主要由两个一个是k表示矩阵连乘的个数，第二个是i表示矩阵的个数。 确定状态变量：dp[k][i]。表示连乘为k的时候，第i个矩阵开始的最优的乘积方式。 确定状态转移...

凸多边形最优三角剖分凸多边形最优三角剖分-动态规划问题描述给定凸多边形P={v0，v1，… ，vn-1}，以及定义在由凸多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分，使得该三角剖分所对应的权，即三角剖分中诸三角形上权之和为最小。 问题分析 若凸(n+1)边形P={v0,v1,…,vn}的最优三角剖分T包含三角形v0vkvn，1≤k≤n-1，则T的权为3个部分权的和：三角形v0vkvn的权，子多边形{v0,v1,…,vk}和{vk,vk+1,…,vn}的权之和 由T所确定的这2个子多边形的三角剖分也是最优的。 因为若有{v0,v1,…,vk}或{vk,vk+1,…,vn}的更小权的三角剖分将导致T不是最优三角剖分的矛盾。 算法原理定义$t[i][j]，1≤i<j≤n$为凸子多边形{vi-1,vi,…,vj}的最优三角剖分所对应的权函数值，即其最优值。 为方便起见，设退化的多边形{vi-1,vi}具有权值0。据此定义，要计算的凸(n+1)边形P的最优权值为t[1][n]。 t[i][j]的值可以利用最优子结构性质递归地计算。当j-i...

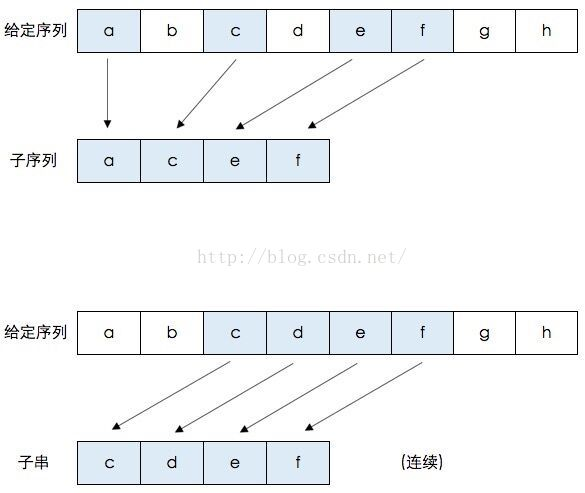
最长公共子序列问题描述求数组A和B的最长公共子序列 问题分析 子序列(subsequence)： 一个特定序列的子序列就是将给定序列中零个或多个元素去掉后得到的结果(不改变元素间相对次序)。例如序列<A,B,C,B,D,A,B>的子序列有：<A,B>、<B,C,A>、<A,B,C,D,A>等。 公共子序列(common subsequence)： 给定序列X和Y，序列Z是X的子序列，也是Y的子序列，则Z是X和Y的公共子序列。例如X=[A,B,C,B,D,A,B]，Y=[B,D,C,A,B,A[，那么序列Z=[B,C,A]为X和Y的公共子序列，其长度为3。但Z不是X和Y的最长公共子序列，而序列[B,C,B,A]和[B,D,A,B]也均为X和Y的最长公共子序列，长度为4，而X和Y不存在长度大于等于5的公共子序列。对于序列[A,B,C]和序列[E,F,G]的公共子序列只有空序列[]。 最长公共子序列：给定序列X和Y，从它们的所有公共子序列中选出长度最长的那一个或几个。 子串： 将一个序列从最前或最后或同时删掉...

最长回文串问题描述给你一个字符串 s，找到 s 中最长的回文子串。 问题分析策略选择算法设计 问题分解划分阶段：规模增长的方向有两个，第一个是最长回文串的长度，第二个是字符串的长度。 确定状态变量dp[i][j]。表示长度为i，以j为起点的字符串是否是回文串。 确定状态转移方程。长度减2，起始位置为j+1的回文字符串。$$dp[i][j]=dp[i-2][j+1] and s[j]==s[j+1-1]$$ 确定边界实现过程。i增长的边界是n，表示最大长度为n，i=0,和i=1时，值都初始化为1；j增长的边界是0到n-i 算法分析 时间复杂度O(n^2) 空间复杂度O(n^2) 算法实现1234567891011121314151617181920212223242526272829class Solution {public:// 思路1 动态规划 string longestPalindrome(string s) { int n=s.size(); if(n==0)re...

作业调度问题 参考文献 https://zhuanlan.zhihu.com/p/30705914 问题描述有n个作业需要在2台机器M1 和M2组成的流水线上完成加工。每个作业都必须先在 M1 上加工，然后在 M2 上加工。M1和M2加工作业i所需的时间分别记作 a_i和b_i，每台机器同一时间最多只能执行一个作业。 请确定这n个作业的最优加工顺序，使得从第一个作业在机器上开始加工，到最后一个作业在机器上加工完成所需的时间最少。 问题分析算法设计 johnson不等式。满足min{bi,aj}>= min{bj,ai}则表示i和j满足johnson不等式。则意味着i在j前执行，不会使的结果变坏。 查参考文献。 算法分析 时间复杂度O(nlogn)按json不等式排序的时间复杂度。 算法实现

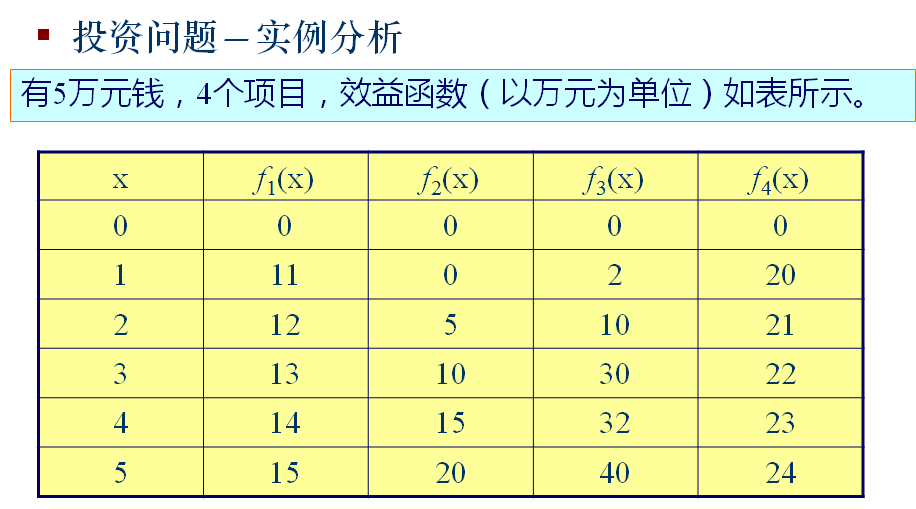
投资问题问题描述m元钱，n个项目。f_i(x)表示x元钱投入项目i的效益。求最大效益。 问题分析算法设计 问题分解划分阶段：规模增长的方向有两个。第一个是投资的金额想，第二个是项目选择k。x,k阶段。 确定状态变量dp[x][k]表示投资x，第k个项目的最大收益。 确定状态转移方程。 状态转移过程。 算法效率 O(n*m^2) 算法实现

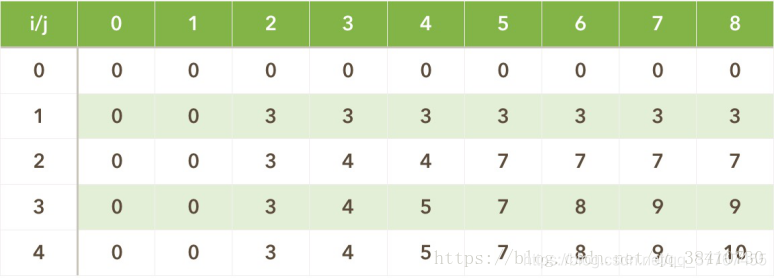
背包问题1 01 背包问题问题描述有N个物品，它们有各自的体积和价值，现有给定容量的背包c，如何让背包里装入的物品具有最大的价值总和？ N=4i 1,2,3,4w 2,3,4,5v 3,4,5,6c=8 问题分析策略选择算法设计有两种动态规划的思路，本质上是一致的。背包的容量增长作为第一维，或者物品的数量增长作为第一维。 当背包的容量作为第一维的时候。背包容量为行，物品增长为列。 问题分解划分阶段。背包容量容量为i,物品选择为j 确定状态dp[i][j]表示背包容量为i的情况下，第j个物品放入或者不放入的最大价值。 确定状态转移方程。分两种情况讨论。当背包容量为i时，第j个物品放入和第j个物品不放入。 $$dp[i][j]=max(dp[i][j-1],dp[i-w[i]][j-1])$$ 当物品的增长作为第一维的时候。物品增长为行，背包容量为列 问题分解划分阶段：2个规模增长方向。背包的容量和物品。物品选择i。背包的容量表示为j。第一个阶段表示是否添加物品。第二个阶段是背包容量的增长。 确定状态dp[i][j]表示第i个物品，在背包容量j...

零钱兑换问题描述给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。 假设每一种面额的硬币有无限个。  1234567输入：amount = 5, coins = [1, 2, 5]输出：4解释：有四种方式可以凑成总金额：5=55=2+2+15=2+1+1+15=1+1+1+1+1 问题分析 典型的动态规划 典型的完全背包问题 策略选择 动态规划 采取两个方向上的动态规划。两个方向上的动态规划是非等价独立的。 数组矩阵线性数据结构 算法设计 阶段划分：规模增长的方向有两个。第一个规模增长的方向是硬币的种类。第二个规模增长的方向是金钱的总量。 状态变量dp[i][j]表示使用第i个硬币，达到j分钱所有的可能。 状态转移方程 if k*coins[i]== amount dp[i][j]++; if kcoins[i]<amount dp[i][j]+=dp[i-1][j-kconis[i]] foreac...

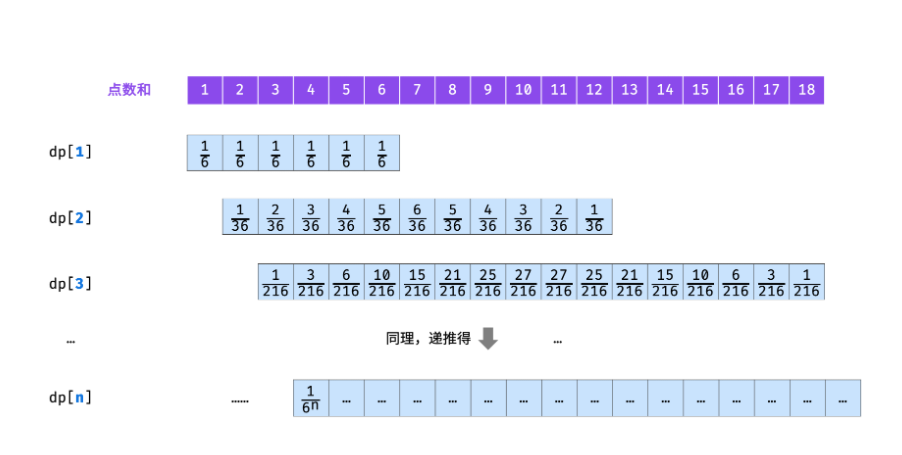
n个骰子的点数 生成幂集的循环方法。完全一致，也是动态规划问题。 1 n个骰子的点数问题描述 把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。你需要用一个浮点数数组返回答案，其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。 示例 1: 123456输入: 1输出: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]示例 2:输入: 2输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778] 问题分析策略选择算法设计 使用动态规划解决问题一般分为三步： 确定状态变量 确定状态转移方程 边界处理 表示状态 分析问题的状态时，不要分析整体，只分析最后一个阶段即可！因为动态规划问题都是划分为多个阶段的，各个阶段的状态表示都是一样，而我们的最终答案在就是在最后一个阶段。 通过题目我们知道一共投掷 n 枚骰子，那最后一个阶...

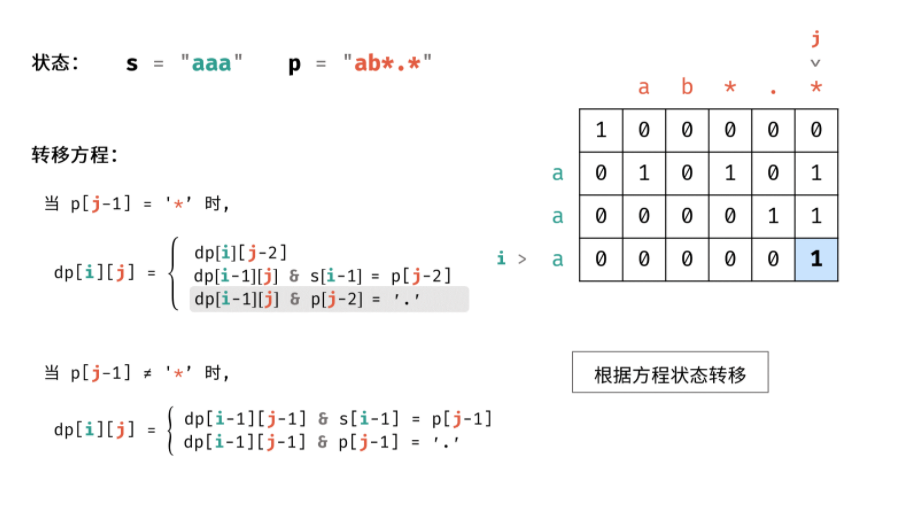
正则表达式匹配问题1 正则表达式匹配问题描述 请实现一个函数用来匹配包含’.‘和’*‘的正则表达式。模式中的字符’.‘表示任意一个字符，而’*‘表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串”aaa”与模式”a.a”和”abaca”匹配，但与”aa.a”和”ab*a”均不匹配。 问题分析 可以使用动态规划。将字符串的规模增长的方向和pattern规模增长的方向，作为动态变化的方向。状态变量表示当前的正则表达式，能够与之匹配。当规模发生变化时，保证字符串-1和正则表达式-1能够匹配。其实在这里感觉规模增长的方向，确实是有两个。但是状态变量的设置比较精巧。 这与最长公共子序列，完全是同一类问题。都是两个方向的动态规划规模增长。包括str和pattern两个方向。 问题分类 字符串匹配问题 动态规划 递归 选择策略 动态规划 算法设计 设s的长度为n ，p 的长度为 m ；将 s 的第 i 个字符记为$s_i$，p 的第 j个字符记为 $p_j$ ，将 s 的前 i 个字符组成的子字符串记为s[:i] , 同理将 p 的...