Estom的博客

指派问题1 指派问题-分支限界问题分析有n项任务要完成，恰好有n个人可以分别去完成其中每一项，但由于任务性质和个人专长不同，因此个人去完成不同的任务的效率（或所费时间）就有差别，由此提出下述问题：应当指派哪个人哪项任务使总的效率为最高（或花费的总时间为最小）？ 一个指派问题给出系数矩阵，或称效率矩阵，矩阵的元素cij(>0) (i, j=1, 2,…, n)表示指派第i人去完成第j向任务的效率（或时间，成本等）。解题时，我们引入0-1变量xij，令 xij=1，当指派第i人去完成第j项任务时， =0,当不指派第i人去完成第j项任务时 算法原理-匈牙利法指派问题最优解的性质：如果从系数矩阵（cij）的一行（列）各元素分别减去该行（列）的最小元素，得到新矩阵（bij） 。那么，以（bij）为系数矩阵的指派问题的最优解（xij）和原问题的最优解相同。

随机化算法随机算法的概述 将算法必须对所有可能的输入都正确地求解问题的条件放宽，只要求它的可能不正确性解能够相对安全地忽略掉，比如说它的出现可能性非常低;而且也不要求对于特定的输入，算法的每一次运行的输出都必须相同。 随机算法可以做如下定义：它是在接收输入的同时，为了随机选择的目的，还接收一串随机比特流并且在运行过程中使用该比特流的算法。 一个随机算法在不同的运行中对于相同的输入可以有不同的结果。由此得出对于相同的输入两次不同的随机算法的执行时间可能不同。 随机算法的优点 首先，较之那些我们所知的解决同一问题最好的确定性算法，随机算法所需的运行时间或空间通常常小一些； 其次，观察迄今为止已经发明的各种随机算法，我们发现这些算法总是易于理解和实现。 1 伪随机数伪随机数的产生$$\begin{cases} a_0=d\ a_n=(ba_{n-1}+c) mod m\end{cases}$$ 其中$a\geq 0,b\geq0,d\geq m,d$是随机序列种子。 2 数值随机化算法3 舍伍德算法 确定性算法随机化。 4 蒙特卡洛算法 蒙特...

近似算法1 近似算法概念 不同的近似算法有各种各样的复杂度，但其中许多算法都是基于特定问题的直观推断贪婪算法。直观推断是一种来自于经验而不是来自于数学证明的常识性规则。如果我们使用的算法所给出的输出仅仅是实际最优解的一个逼近，我们就会想知道这个逼近有多精确。 近似算法精度 对于一个对某些函数 f 最小化的问题来说，可以用近似解的相对误差规模$$re(S_a)=\frac{f(S_*)}{f(S^a)}$$ 近似算法的性能 对于问题的所有实例，它们可能的r(sa)的最佳（也就是最低）上界，被称为该算法的性能比，计作RA。 性能比是一个来指出近似算法质量的主要指标，我们需要那些RA尽量接近1的近似算法。

遗传算法1 遗传算法概述步骤 随机产生一组初始个体构成初始种群，并评价每一个体的适配值（fitness value）。 判断算法收敛准则是否满足。若满足则输出搜索结果；否则执行以下步骤。 根据适配值大小以一定方式执行复制操作。 按交叉概率pc执行交叉操作。 按变异概率pm执行变异操作。 返回步骤2。 遗传算法的特点遗传算法利用生物遗传和进化的思想实现优化 对问题参数编码成“染色体”后进行进化操作，而不是针对参数，这使得它不受某些函数约束条件的限制，如连续性、可导性等； 搜索过程是从问题解的一个集合开始的，而不是从单个个体开始的，具有隐含并行搜索特性，从而大大减小了陷入局部极小的可能； 具有全局搜索能力； 适应性、收敛性。

邻域结构优化算法1 算法概述算法原理 利用邻域结构进行逐步优化的局部搜索算法： 算法从一初始可行解 s 出发，利用状态发生器持续地在s 的领域中搜索更好的解，若能找到更优解，则以其替代s 成为新的当前解，然后重复上述过程，直至终止条件满足。

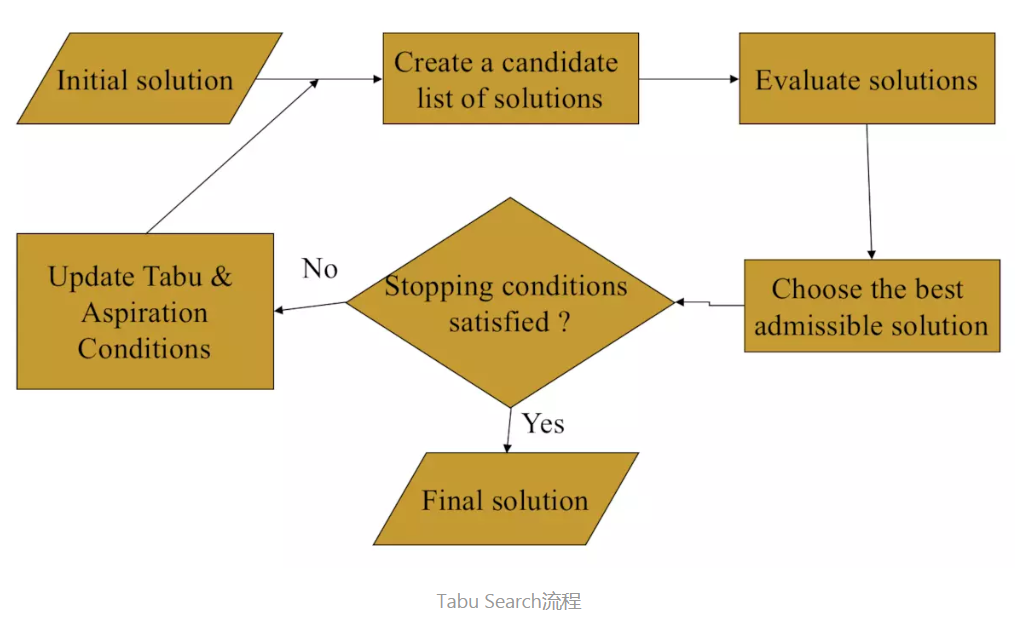
禁忌搜索算法1 算法说明算法概述 禁忌搜索（TS）是对局部邻域搜索的一种扩展，是一种全局优化算法。TS算法通过引入一个禁忌表和相应的禁忌准则来避免局部迂回，并通过“渴望准则”来挽救某些被禁忌的相对优化解，进而保证全局的有效搜索以实现全局优化。 标记对应已搜索到的局部最优解的一些对象，并在进一步的迭代搜索中尽量避开这些对象，但不是绝对禁止循环，从而保证对不同的有效搜索途径的探索。 基本思想 给定一个当前解（初始解）和一种邻域结构，在当前解的邻域中确定若干候选解； 若最佳候选解对应的目标植优于 “best so far” ，则忽视其禁忌特性，用其替代当前解和“best so far”值，并将相应的对象加入禁忌表，同时修改禁忌表中各对象的禁忌任期； 若不存在上述候选解，则选择在候选解中非禁忌的最佳状态为新的当前解，而无视它与当前解的优劣，同时将相应的对象加入禁忌表，并修改禁忌表中各对象的任期； 重复上述迭代搜索过程，直至满足停止条件。 算法原理邻域 对于组合优化问题，给定任意可行解x，x∈D，D是决策变量的定义域，对于D上的一个映射：N：x∈D→N(x)∈2(D) 其中2(D)...

递归与迭代。 参考文献 递归详解 递归算法讲解 递归算法的理解 递归的本质 由于递归与迭代的特殊性。在这里单独列出一种思想。递归与迭代思想，用来处理所有的重复的操作。如分治法的相同子操作、动态规划的相同子操作、深度优先搜索、广度优先搜索的相同子操作。 1 递归法概述基本思想 直接或间接的调用自身的算法称为递归算法。用函数自身给出定义的函数称为递归函数。 递归的基本思想就是把规模大的问题转化为规模小的相似的子问题来解决。 递归的数学模型其实就是数学归纳法。可以用反向递推式表示递归的过程。（使用正向递推式表示循环的过程） 线性收缩递归算法 递推关系式 $$T(n)=\begin{cases} o(1) & n=1 \ \sum_{i=1}^k a_iT(n-i)+f(n) & n>1\end{cases}$$ 求解递推关系式$$T(n)=a^{n-1}T(1)+\sum_{i=2}^na^{n-i}f(i)$$ 关系式说明 等比收缩递归算法 递推关系式$$T(n)=\be...