B类:数据结构算法
文章
0 数据结构算法说明
概述 一个问题。强相关的标签有三个。属于哪一类问题。使用哪些算法思想。问题属于哪一种数据结构。因为vscode的文件组织方式为树形结构。只能支持单一索引,无法支持多种类别的标签索引。 所以最终决定。应该将不断增长的爆炸性问题。转移到C类:问题算法中。主要用来记录在解决问题中的思考和见解。根据问题类型对算法分类。记录算法。 分类说明 与数据结构强相关的算法 与算法思想强相关的算法 与问题目标强相关的算法 命名说明 以某一类算法的名称命名,而不是某一个算法命名。收集找到该类别下的相关算法。
1.1 图算法-Dijkstra算法 copy
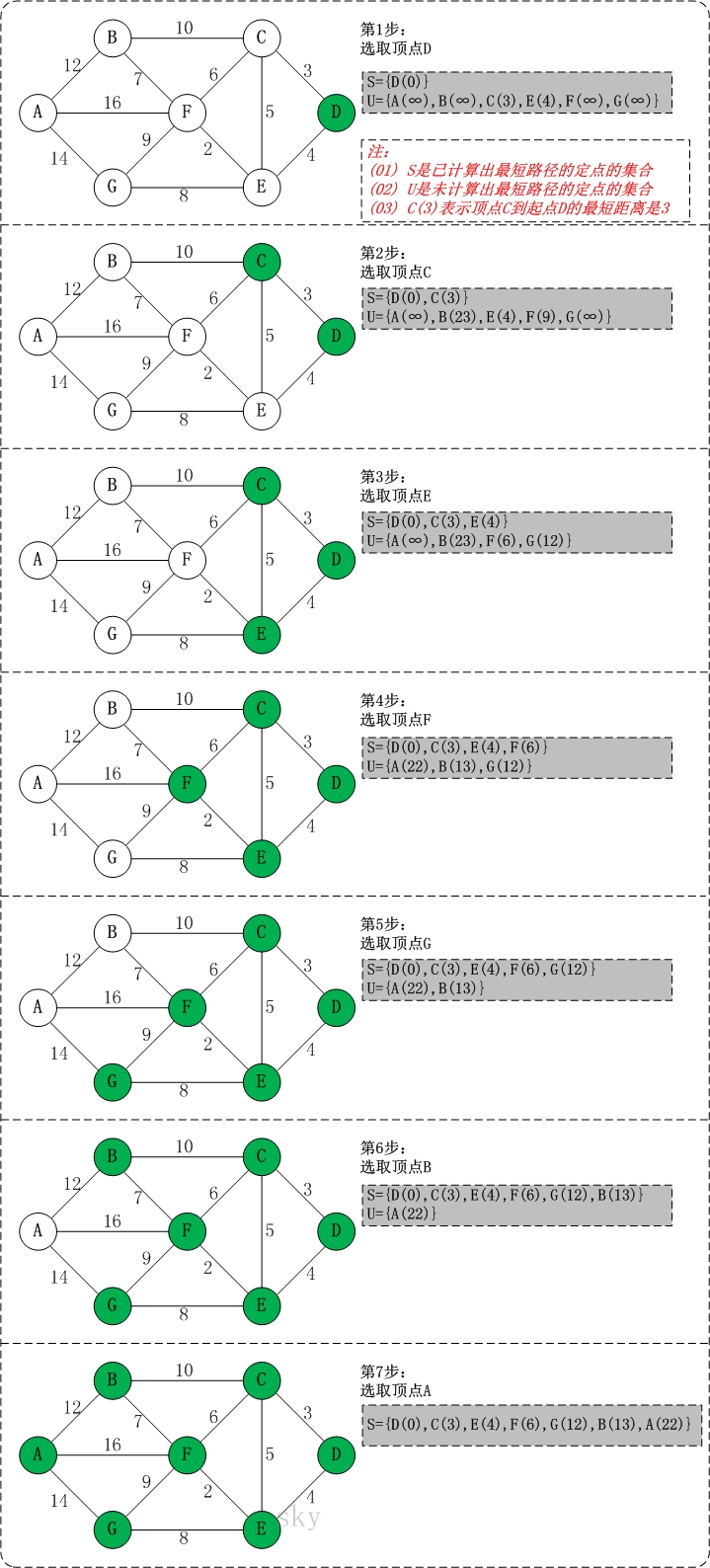
图算法-Dijkstra算法 目录 图算法-Dijkstra算法 图算法-Floyd算法 图算法-Bellman-Ford算法 图算法-Prim算法 图算法-Kruskal算法 参考文献 https://www.cnblogs.com/msymm/p/9769915.html https://blog.csdn.net/jeffleo/article/details/53349825 1 问题分析 最短路径算法。用于单源最短路算法 Dijkstra算法算是贪心思想实现的,首先把起点到所有点的距离存下来找个最短的,然后松弛一次再找出最短的,所谓的松弛操作就是,遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近,如果更近了就更新距离,这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。 2 算法原理 通过Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。 此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。 初始时,S...
1.2 图算法-Floyd算法
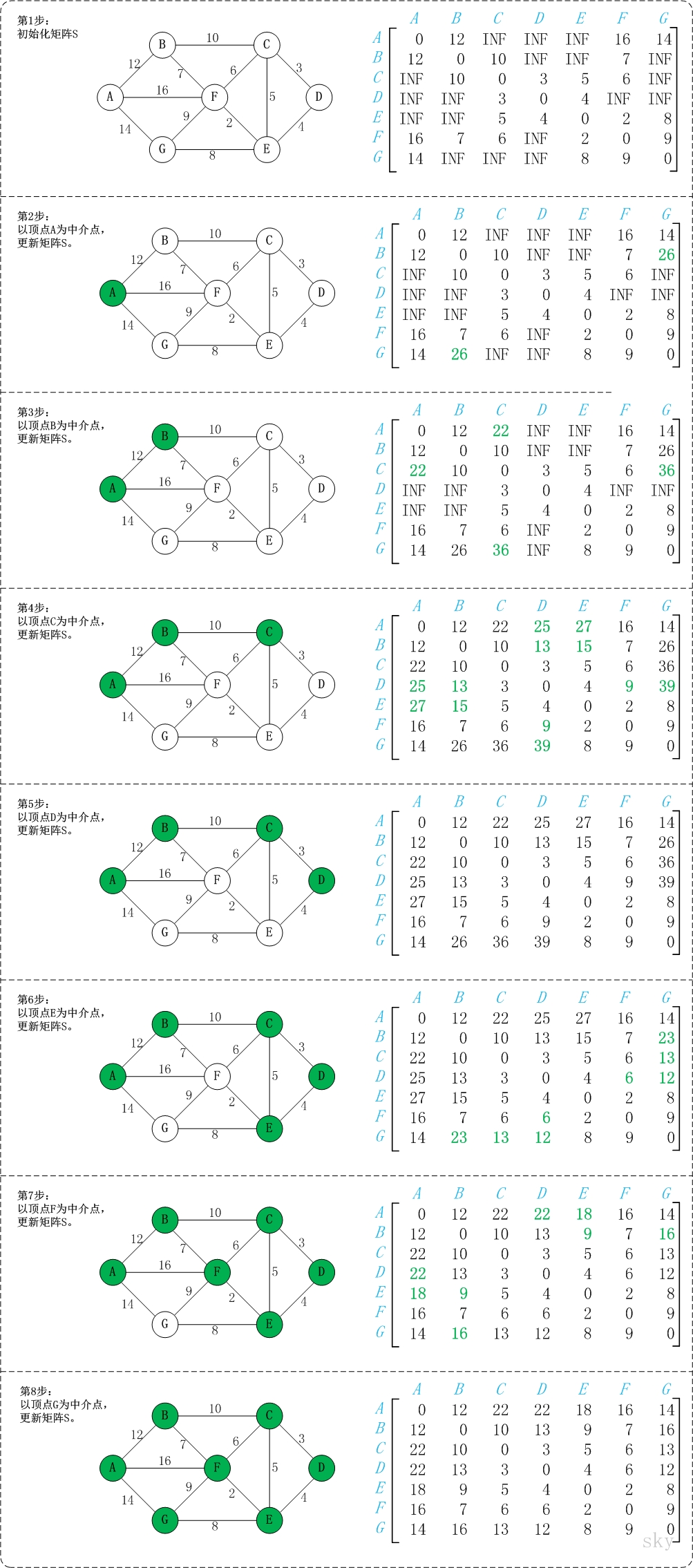
图算法-Floyd算法 目录 图算法-Dijkstra算法 图算法-Floyd算法 图算法-Bellman-Ford算法 图算法-Prim算法 图算法-Kruskal算法 参考文献 https://www.jianshu.com/p/f73c7a6f5a53 https://blog.csdn.net/jeffleo/article/details/53349825 1 问题分析 Floyd算法是一个经典的动态规划算法,它又被称为插点法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。 Floyd算法是一种利用动态规划的思想寻找给定的加权图中多源点最短路径的算法 ,算法目标是寻找从点i到点j的最短路径。 2 算法原理 Floyd算法的基本思想:可以将问题分解: 第一、先找出最短的距离 第二、然后在考虑如何找出对应的行进路线。 以后再整理一下文字内容 3 算法过程 顶点名称和下标的对应 A B C D E F G 0 1 2 3 4 5 6 弗洛伊德算法定义了两个二维矩阵 矩阵D记录顶点间的最小路...
1.3 图算法-Bellman-Ford算法
图算法-Bellman-Ford算法 目录 图算法-Dijkstra算法 图算法-Floyd算法 图算法-Bellman-Ford算法 图算法-Prim算法 图算法-Kruskal算法 bellman ford 和 SPFA两个算法等到以后再学吧。我赌十块不需要。等到下次在复习的时候完善这两个算法,已经没时间了 参考文献 https://www.cnblogs.com/lfri/p/9521271.html https://blog.csdn.net/qq_35644234/article/details/61614581 这两个博客够了
1.4 图算法-Kruskal算法
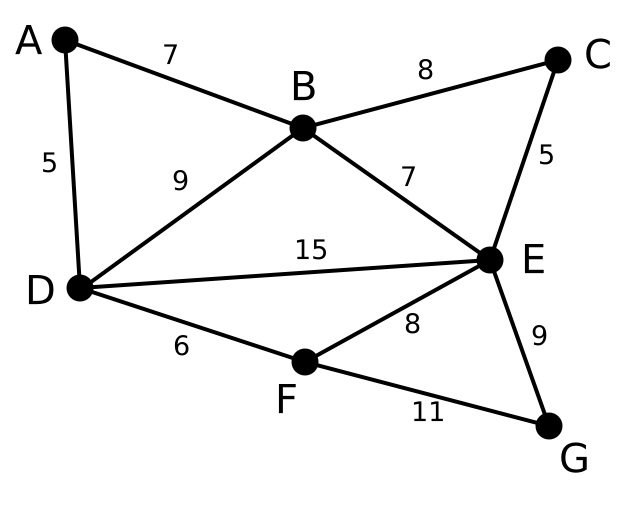
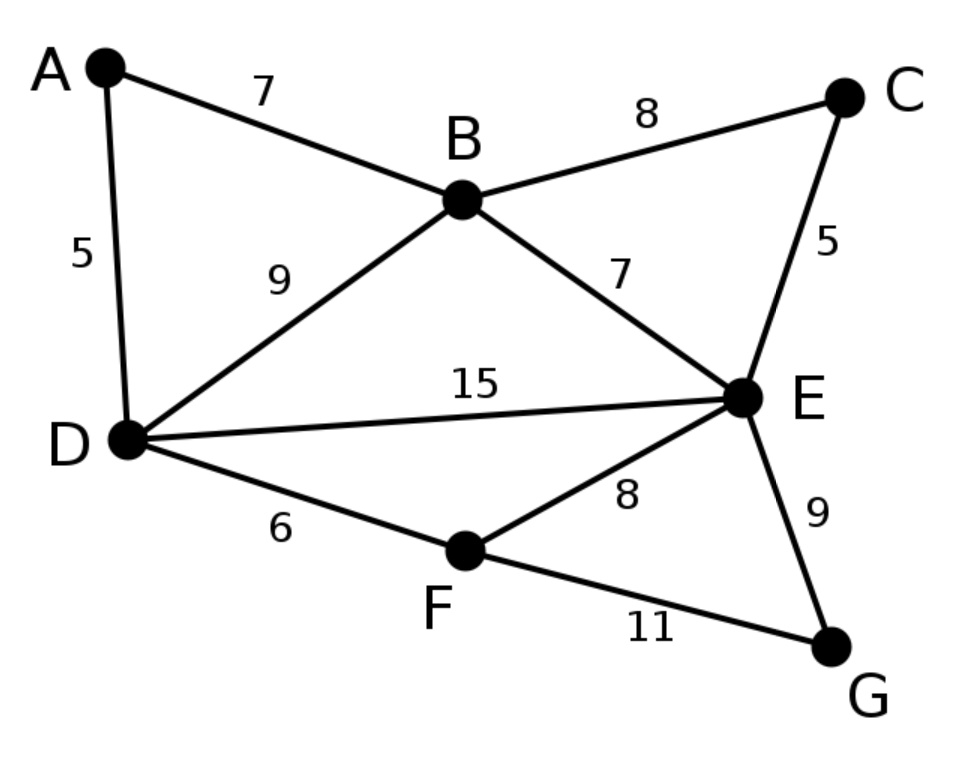
图算法-Dijkstra算法 目录 图算法-Dijkstra算法 图算法-Floyd算法 图算法-Bellman-Ford算法 图算法-Prim算法 图算法-Kruskal算法 参考文献https://www.cnblogs.com/ggzhangxiaochao/p/9070873.html 1 问题描述 Kruskal算法是一种用来寻找最小生成树的算法,由Joseph Kruskal在1956年发表。 用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪婪算法的应用。和Boruvka算法不同的地方是,Kruskal算法在图中存在相同权值的边时也有效。 当点少,但是关系复杂的时候,使用prim算法,进行点的贪心。 当点多,但是关系很稀疏的时候,使用kruskal算法那,进行边的贪心 2 算法原理 记Graph中有v个顶点,e个边 新建图Graphnew,Graphnew中拥有原图中相同的e个顶点,但没有边 将原图Graph中所有e个边按权值从小到大排序 循环:从权值最小的边开始遍历每条边。if这条边连接的两个节点于图Graphnew中不...
1.5 图算法-Prim算法
图算法-Prim算法 目录 图算法-Dijkstra算法 图算法-Floyd算法 图算法-Bellman-Ford算法 图算法-Prim算法 图算法-Kruskal算法 参考文献 https://www.cnblogs.com/ggzhangxiaochao/p/9070873.html 1 问题分析 普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (graph theory)),且其所有边的权值之和亦为最小。 主要思想是基于顶点的贪心思想。 2 算法原理 输入:一个加权连通图,其中顶点集合为V,边集合为E; 初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空; 重复下列操作,直到Vnew = V: 在集合E中选取权值最小的边<u, v>,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任...
2.1 深搜与广搜
树的遍历1 树的子结构 输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构).B是A的子结构, 即 A中有出现和B相同的结构和节点值。 链接 2 树的镜像 请完成一个函数,输入一个二叉树,该函数输出它的镜像。 链接 3 对称的二叉树 请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。 链接 4 二叉搜索树的第k大节点 给定一棵二叉搜索树,请找出其中第k大的节点。 示例 1: 12345678输入: root = [3,1,4,null,2], k = 1 3 / \ 1 4 \ 2输出: 4示例 2: 链接 5 二叉树的深度 输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。 例如: 12345678给定二叉树 [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7返回它的最大深度 3 。 链接 6 平衡二叉树 输入一棵二叉树的根节...
2.2 树形变换
1 二叉树与双向链表问题分析 输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。 链接 1.1 二叉树与双向链表——左旋右旋 借鉴了构建二叉平衡树的内容。可以自己完成以下二叉平衡树试试。 算法设计 通过左旋右旋操作实现树的旋转。最终旋转成一个倒V树。 算法分析 时间复杂度O(n) 空间复杂度O(n) 算法实现123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384class Solution {public: Node* treeToDoublyList(Node* root) { // 类似于二叉平衡树的左旋右旋。 if(root==nullptr){ retu...