Estom的博客

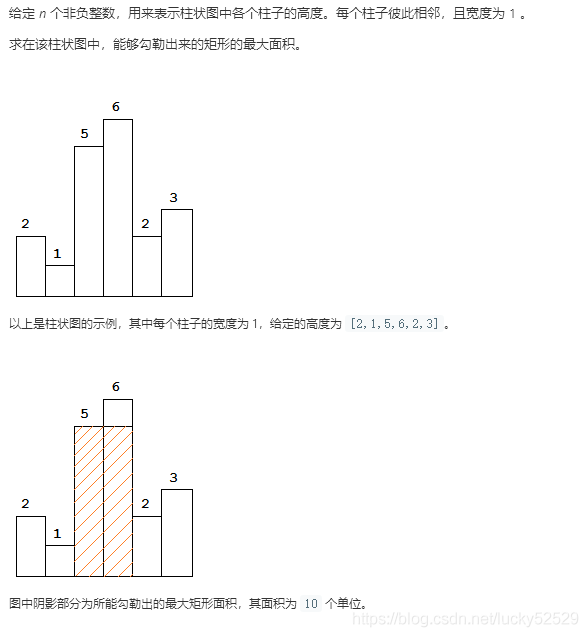
单调栈 用来解决局部顺序问题 柱形图问题多使用单调栈。 下边是对柱形图问题的总结。 视野总和：利用了栈内元素的数量计算问题。 柱形图中的最大矩形：利用的是出栈序列。这组序列构成了可能的最大矩形。 盛最多水的容器：利用了反向贪心思想。 接雨水问题：单调栈解法也是利用了出栈序列。这个序列的左右边界能够形成一个容器。双指针解法利用了反向贪心思想。 接雨水问题2 其它类型的单调栈 求最大区间：利用的出栈的序列。表示一个可能的最大值区间。 132模式：利用了其有序性。 1 视野总和问题描述 有n个人站队，所有的人全部向右看，个子高的可以看到个子低的发型，给出每个人的身高，问所有人能看到其他人发现总和是多少。 123输入：4 3 7 1输出：2解释：个子为4的可以看到个子为3的发型，个子为7可以看到个子为1的身高，所以1+1=2 问题分析 问题分类: 思路：观察题之后，我们发现实际上题目转化为找当前数字向右查找的第一个大于他的数字之间有多少个数字，然后将每个结果累计就是答案，但是这里时间复杂度为O(N^2)，所以我们使用单调栈来解决这个问题。 策略选择 数据结构：单调栈 算...

1 队列的最大值问题描述 请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。 若队列为空，pop_front 和 max_value 需要返回 -1 示例 1： 1234输入: ["MaxQueue","push_back","push_back","max_value","pop_front","max_value"][[],[1],[2],[],[],[]]输出: [null,null,null,2,1,2] 链接 问题分析策略选择 数据结构：单调队列 算法思想：后入的较大值，会把之前的较大值排除。但是后入的次大值，不会将之前的最大值排出队列。所以维护两个队列，一个用来删除元素，一个用来找到最大值（单调队列） 算法设计 本算法基于问题的一个重要性质：当一个元素进入队列的时候，它前面所有比它小的元素就不会再对答案产生影响。 举个...

接雨水问题 这个问题也太经典了，能用的这些思路，也太神奇了。 1 接雨水问题给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。 上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的直方图，在这种情况下，可以接 6 个单位的水（蓝色部分表示水）。 感谢 Marcos 贡献此图。 示例: 链接 1234输入: [0,1,0,2,1,0,1,3,2,1,2,1]输出: 6 问题分析 问题抽象 问题分类：线性数组 1.1 接雨水问题——动态规划策略算则 动态规划 算法设计 左扫一遍，求每个位置的左最大值。 右扫一遍，取每个位置的右最大值。 取两个最大值的最小值。作为该位置能接雨水的高度。 算法分析 时间复杂度O(n) 空间复杂度O(n) 算法实现12345678910111213141516171819202122class Solution {public: int trap(vector<int>& height) { int n=height....

栈的弹出序列问题描述输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如，序列 {1,2,3,4,5} 是某栈的压栈序列，序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列，但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。   示例 1： 12345输入：pushed = [1,2,3,4,5], popped = [4,5,3,2,1]输出：true解释：我们可以按以下顺序执行：push(1), push(2), push(3), push(4), pop() -> 4,push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1 示例 2： 123输入：pushed = [1,2,3,4,5], popped = [4,3,5,1,2]输出：false解释：1 不能在 2 之前弹出。 链接 问题分析 之前入栈的元素，在之后只能以逆序出现。也就是说，逆序之后的数字，都是逆序。 策略选择算法设计算法分析算法实现...

反转链表1 从尾到头打印链表内容问题描述输入一个链表的头节点，从尾到头反过来返回每个节点的值（用数组返回）。 问题分类 线性数据结构 枚举法 排序问题 问题分析1.1 从尾到头打印链表内容——辅助栈策略选择 数据结构：链表、栈、数组 算法思想：枚举法 可以利用栈的先进后出特性。 算法设计 入栈： 遍历链表，将各节点值 push 入栈。（Python​ 使用 append() 方法，​Java​借助 LinkedList 的addLast()方法）。 出栈： 将各节点值 pop 出栈，存储于数组并返回。（Python​ 直接返回 stack 的倒序列表，Java ​新建一个数组，通过 popLast() 方法将各元素存入数组，实现倒序输出）。 算法分析 时间复杂度O(n) 空间复杂度O(n) 算法实现1234567891011121314vector<int> reversePrint1(ListNode* head) { stack<int> s; vector<int> v; ListNode * temp...

链表与双指针1 链表中的倒数第k个节点问题描述 输入一个链表，输出该链表中倒数第k个节点。为了符合大多数人的习惯，本题从1开始计数，即链表的尾节点是倒数第1个节点。例如，一个链表有 6 个节点，从头节点开始，它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。 问题分析 典型的双指针问题 问题分类 数组与链表 双指针问题 策略选择 蛮力法 算法流程 两个一样快的指针。相距k个距离。 一个到达终点，另一个则为倒数第k个节点 算法分析 时间复杂度O(n) 空间复杂度O(1) 算法实现123456789101112ListNode* getKthFromEnd(ListNode* head, int k) { ListNode* first=head; ListNode* second=head; while(--k){ second=second->next; } while(second->next){ second = se...

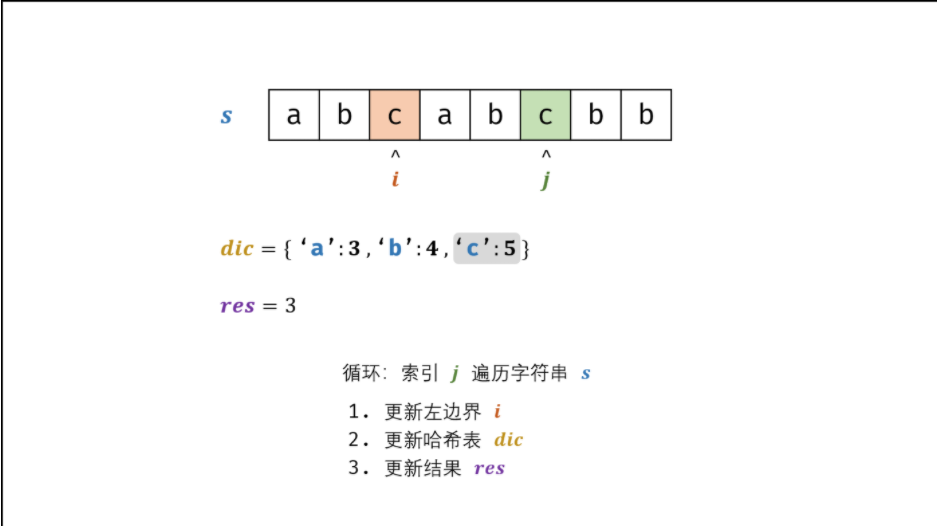
数组与滑动窗口1 最长不含重复字符的子字符串——滑动窗口问题描述 请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。 问题分析问题分类算法设计 哈希表 dicdic 统计： 指针 jj 遍历字符 ss ，哈希表统计字符 s[j]s[j] 最后一次出现的索引 。 更新左指针 ii ： 根据上轮左指针 ii 和 dic[s[j]]dic[s[j]] ，每轮更新左边界 ii ，保证区间 [i + 1, j][i+1,j] 内无重复字符且最大。$$i=max(dic[s[j]],i)$$ 更新结果 res ： 取上轮 res 和本轮双指针区间 [i + 1,j][i+1,j] 的宽度（即 j - ij−i ）中的最大值 $$res=max(res,j−i)$$ 算法分析 时间复杂度 O(N)： 其中 N为字符串长度，动态规划需遍历计算 dpdp 列表。 空间复杂度 O(1) ： 字符的 ASCII 码范围为 00 ~ 127，哈希表 dic最多使用 O(128) = O(1) 大小的额外空间。 算法分析 时间复杂度 O(N...

线性区间操作区间操作分类 修改区间值，询问元素值。（差分数组） 修改元素值，访问区间值。（树状数组和线段树） 修改元素值，查询最大最小值。（线段树） 1 数组中的逆序对问题描述在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。 问题分析策略选择 数据结构：线性数组、树状数组 算法思想：用树状数组解决逆序数问题，也是一个经典的做法。树状数组是一种实现了高效查询「前缀和」与「单点更新」操作的数据结构， 算法设计具体的做法是： 先离散化，将所有的数组元素映射到 0、1、2、3… ，这是为了节约树状数组的空间； 从后向前扫描，边统计边往树状数组里面添加元素，这个过程是「动态的」，需要动手计算才能明白思想。 我们可以看出它第i−1 位的前缀和表示「有多少个数比 i 小」。那么我们可以从后往前遍历序列a，记当前遍历到的元素为 $a_i$，我们把$a_i$对应的桶的值自增 1，把 i - 1位置的前缀和加入到答案中算贡献。 我们显然可以用数组来实现这个桶，可问题是如果$a_i$中有很大的元素，比如 10^9我...