线性代数
文章
0 线性代数概述
线性代数线性代数究竟讲了个什么事情?线性方程组、向量、线性空间之间有什么关系?他们与矩阵有什么关系?为什么要在线性代数中讲到矩阵? 1 映射=函数=变换=算子 (在不同领域的不同称呼) 通常我们说 变换(transformation)时,实际上指的是函数(function)f ,也成为一个算子或者映射,给它一定的输入,它会产生相应的输出。 在线性代数的场景中,变换(transformation)可以想象为输入某个向量,然后输出另一个向量的过程。 2 线性方程、向量空间、线性空间关系是同一个东西的不同表述。 线性方程的系数表示的输入向量,多组$[x_1,\cdots,x_n]$表示多组算子。$[y_1,y_2,\cdots,y_n]$表示变换后的结果。(后续补充:感觉系数像是算子,未知量像解空间) 向量空间。由多个线性无关的向量组成的向量组,称为向量空间。每一个向量表示一个算子。 线性空间。有多个线性无关的基底组成的线性空间。每一个基底表示一个算子。 3 线性变换的表示一般来说,方阵能描述任意线性变换。线性变换,在一个线性空间中,将一个向量依次乘一...
1 矩阵行列式
行列式1 行列式与线性方程组线性方程程组$$\begin{cases} a_{11}x_1+a_{12}x_2=b_1\ a_{21}x_1+a_{22}x_2=b_2\end{cases}\$$ 行列式含义$$\begin{vmatrix} a_{11} & a_{12}\ a_{21} & a_{22}\end{vmatrix}= a_{11}a_{22}-a_{12}a_{21}\\begin{vmatrix} a_{11} & a_{12} & a_{13}\ a_{21} & a_{22} & a_{23}\ a_{31} & a_{32} & a_{33}\end{vmatrix}\= a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32}-a_{13}a_{21}a_{32}$$ 行列式表...
2 矩阵基本运算
矩阵及其运算1 矩阵概念定义:矩阵$$A=\begin{bmatrix} {a_{11}} & {a_{12}} & {\cdots} & {a_{1 n}} \ {a_{21}} & {a_{22}} & {\cdots} & {a_{2 n}} \ {\vdots} & {\vdots} & {\ddots} & {\vdots} \ {a_{m 1}} & {a_{m 2}} & {\cdots} & {a_{m n}}\end{bmatrix}$$ m行n列矩阵,$m \times n$矩阵,记作$A_{m\times n}$ 矩阵中的第i行第j列称为A的元素,记作$a_{ij}$ 矩阵分类 实矩阵、复矩阵:元素都是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵...
3 矩阵初等变换
矩阵的初等变换1 矩阵的初等变换初等变换的定义矩阵的初等行变换$A\sim^r B$、初等列变换$A\sim^c B$ 对调两行 数乘某一行 某一行元素的k倍加到另外一行 初等行变换与初等列变换统称初等变换。记作$A\sim B$ 初等变换的性质 反身性$A \sim A$ 对称性$A\sim B,B\sim A$ 传递性$A\sim B,B\sim C,A\sim C$ 初等变换的形式 行阶梯形式:阶梯型。 行最简形式:每一行第一个非零元素为1,且该列其他元素为零。 标准形式:行变换后,进行列变换,到达行最简形式,列最简形式。左上角单位阵$$F=\begin{bmatrix} E_r & 0\ 0 & 0\end{bmatrix}_{m\times n}$$ 初等变换的乘积表示 $A\sim^r B$的充要条件存在m阶可逆矩阵P,使$PA = B$ $A\sim^c B$的充要条件存在n阶可逆矩阵Q,使$AQ = B$ $A\sim B$的充要条件存在m阶可逆矩阵P,存在n阶可逆矩阵Q,使$PAQ =B$ ...
3.1 线性方程组
线性方程组 利用矩阵求解线性方程组的解。
3blue1brown
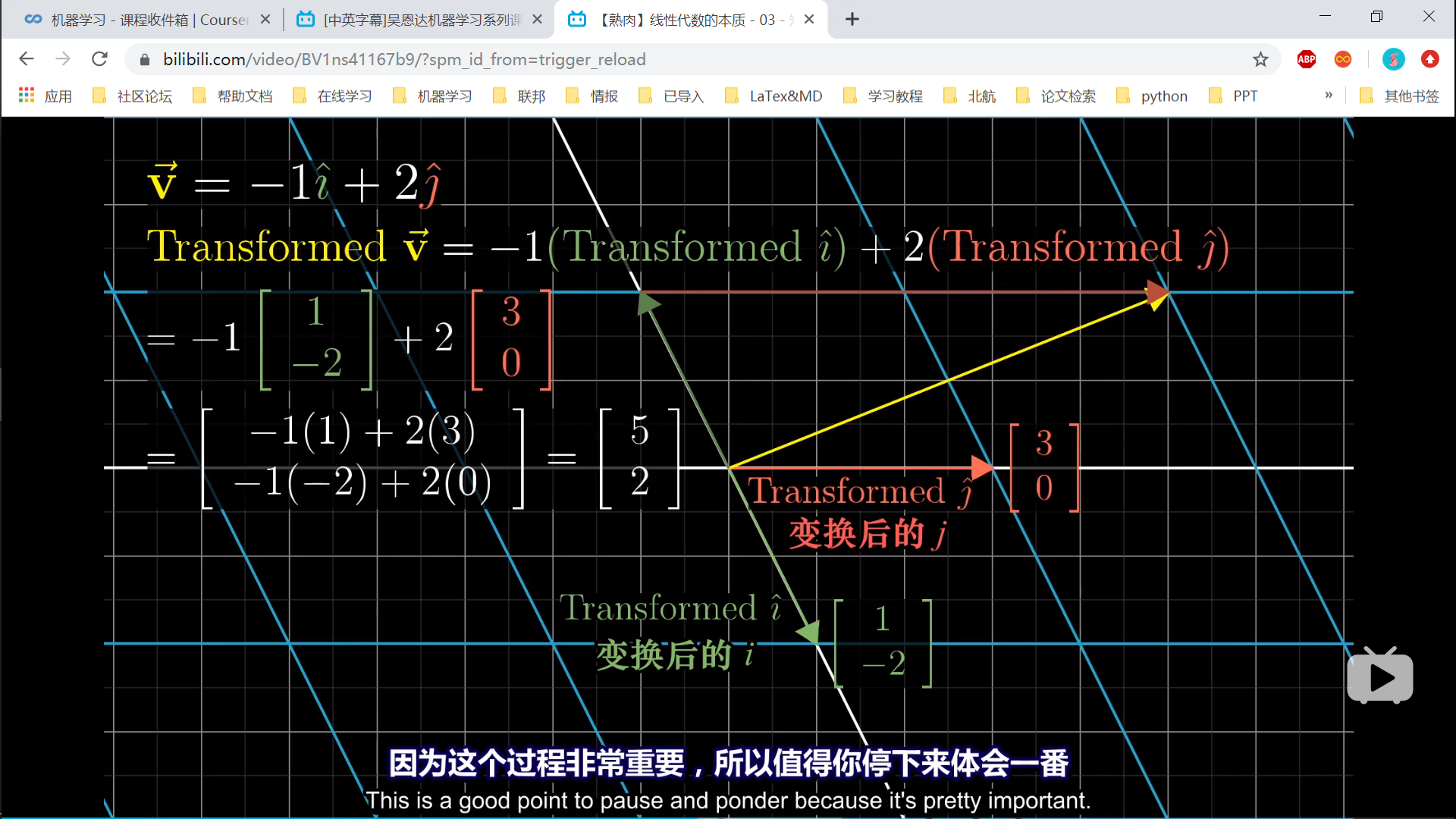
线性代数的本质 宇宙最强系列视频 向量的本质 图形=符号=坐标 线性组合、张成的空间与积 基向量i,j的可以表示向量空间。 任意两个向量的线性组合可以表示平面,称为向量的张成空间 不同的基向量,对向量空间的描述不同。 线性变换 线性变换:保持平行 原来的向量表示,乘以变换后的基向量表示 基向量变换。矩阵表示列向量的个数,列向量的每一个值,都表示向量的一个维度。矩阵的第一个维度,是所有列向量的第一个维度的排列。源向量的每一个维度,代表不同的基向量的scaling,缩放。 线性变换, 变换后的基向量=矩阵的列向量 原向量的每一个维度,都是对基向量的缩放。 目标向量的每一个维度,都是变换后的基向量在这一个维度的缩放的和。 [1,2,3,4]自身是1维数组,维度是4,能描述4个维度的数组。 矩阵乘法 批量的线性变换。 非方阵。行缺失,表示主成分保留,次要维度省略。 非方阵。行增加,表示补充了次要成分。
4 向量空间
向量7 向量运算定义:向量内积$$x=(x_1,\cdots,x_n)^T\y=(y_1,\cdots,y_n)^T\[x,y]=x^Ty=x_1y_1+\cdots+x_ny_n$$[x,y]称为向量的内积。 性质:向量内积 $[x,y]=[y,x]$ $\lambda[x,y]=[\lambda x,y]$ $[x+y,z]=[x,z]+[y,z]$ $x=\overrightarrow{0},=>[x,x]=0\x \not =\overrightarrow{0},=>[x,x]\not =0$ 施瓦茨不等式:$[x,y]^2\geq [x,x]+[y,y]$ 定义:向量长度(范数)$$||x||=\sqrt{[x,x]}=\sqrt{x_1^2+\cdots+x_n^2}$$ 性质:向量长度 非负性:$x=\overrightarrow{0},=>||x||=0\x \not...
5 矩阵相似变换
矩阵相似变换1 特征值和特征向量 应用,方阵的对角化,解微分方程 定义:特征值和特征向量 声明 $$A是n阶矩阵\\lambda 数\x是n维向量$$ 条件特征表达式$$Ax=\lambda x$$ 结论$$\lambda 是矩阵A的特征值\x是矩阵A的特征向量。$$ 性质:特征值特征向量 同一个特征值的所有特征向量的非零线性组合,仍是特征向量。 特征值的性质:$$\lambda_1+\cdots+\lambda_n=a_1+\cdots+a_n\\lambda_1\cdots\lambda_n=|A|=det A$$ 定理:特征值、特征向量、矩阵的线性变换$$\lambda 是矩阵A的特征值,p是属于lambda的特征向量$$ $k\lambda 是kA的特征值,p是kA属于k\lambda的特征向量$ $\lambda^k是A^k的特征值,p是A^k属于\lambda^k的特征向量$ $\frac{1}{\lambda}是A^{-1}的特征值$ $\varphi(A)是A的m次多项式,\varphi(\lambda)是\va...
5.1 二次型
二次型及标准型 二次方程组的矩阵表示,及化简,变为标准型。 1 二次型定义1:二次型 条件$$f(x_1,\cdots,x_n)=a_{11}x_1^2+\cdots+a_{nn}x_n^2\ 2a_{12}x_1x_2+\cdots+2a_{n(n-1)}x_nx_{n-1}\ = \sum_{i,j=1}^na_{ij}x_ix_j$$含有n个变量的二次其次函数称为二次型。 定义2:标准型 条件$$f=k_1y_1^2+\cdots+k_ny_n^2$$只含有平方项的二次型称为标准型。 定义3:规范型 条件$$f=(+|-)y_1^2+\cdots+(+|-)y_n^2$$标准型的系数只能在0,-1,1三个数中取值时,称为规范型 定义4:二次型的矩阵表示$$f=x^TAx\x=\begin{bmatrix} x_1\ \vdots\ x_n\end{bmatrix}A=\begin{bmatrix} a_{11} & \cdots & a_{1n...