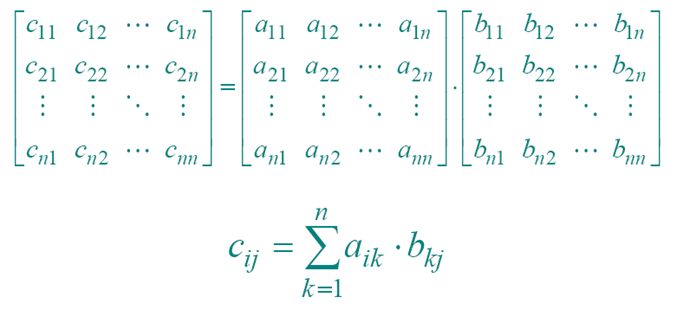Estom的博客

大整数乘法 参考文献 大数乘法的问题及其高效的算法 问题描述 题目描述： 输出两个不超过100位的大整数的乘积。 输入： 输入两个大整数，如1234567 和 123 输出： 输出乘积，如：151851741 数字以字符串的形式给出。 1求 1234567891011121314151617181920 * 2019181716151413121110987654321 的乘积结果 问题分析 所谓大数相乘（Multiplication algorithm），就是指数字比较大，相乘的结果超出了基本类型的表示范围，所以这样的数不能够直接做乘法运算。参考了很多资料，包括维基百科词条Multiplication algorithm，才知道目前大数乘法算法主要有以下几种思路： 模拟小学乘法：最简单的乘法竖式手算的累加型； 分治乘法：最简单的是Karatsuba乘法，一般化以后有Toom-Cook乘法； 快速傅里叶变换FFT：（为了避免精度问题，可以改用快速数论变换FNTT），时间复杂度O(N lgN lglgN)。具体可参照Schönhage–Strassen algorith...

矩阵乘法1 矩阵乘法-蛮力法问题描述 问题分析算法设计问题归结为计算元素C[i,j]。依据定义来计算A和B的乘积矩阵C，则每计算C的一个元素C[i][j]，需要做n次乘法和n-1次加法。C的规模为n*n。 算法分析 时间复杂度O(n^3) 算法实现2 矩阵乘法-STRASSEN算法算法设计算法的基本思想在于以增加加减法的次数来减少乘法次数：用了7次n/2 x n/2 矩阵乘法和18次n/2 x n/2 矩阵的加法 算法过程 将矩阵分块 1234A = a11 a12 a21 a22 B = b11 b12 b21 b22 计算分块矩阵的乘法 1234567d1 = (a11 + a22) (b11 + b22)d2 = (a21 + a22) b11d3 = a11 (b12 – b22)d4 = a22 (b21 –b11)d5 = (a11 + a12) b22d6 = (a21 – a11) (b11 + b12)d7 = (a12 – a22) ( b21 + b22) 将分块矩阵乘法进...

拓扑排序-减治法问题描述考虑五门必修课的一个集合{C1, C2, C3, C4, C5},一个在职的学生必须在某个阶段修完这几门课程。可以按照任何次序学习这些课程，只要满足下面这些条件： C1和C2没有任何先决条件； 修完C1 和C2才能修C3； 修完C3 才能修C4； 修完C3、C4才能修C5； 这个学生每个学期只能修一门课程。 若用一个图来建模，它的顶点代表课程，有向边表示先决条件，该问题为：是否可以按照这种次序列出它的顶点，使得对于图中每一条边来说，边的起始顶点总是排在边的结束顶点之前。 这个问题称为拓扑排序。 如果有向图具有一个有向的回路，该问题是无解的。因此，为了使得拓扑排序成为可能，问题中的图必须是一个无环有向图。 拓扑排序-减治原理基于减（减一）治技术的一个直接实现：重复以下过程： 在余下的有向图中求出一个源，它是一个没有输入边的顶点； 然后把该源和所有从它出发的边都删除。（如果有多个这样的源，可以任意选择一个；如果这样的源不存在，算法停止，因为该问题是无解的） 顶点被删除的次序就是拓扑排序的一个解。 1234567891011121314151617181...

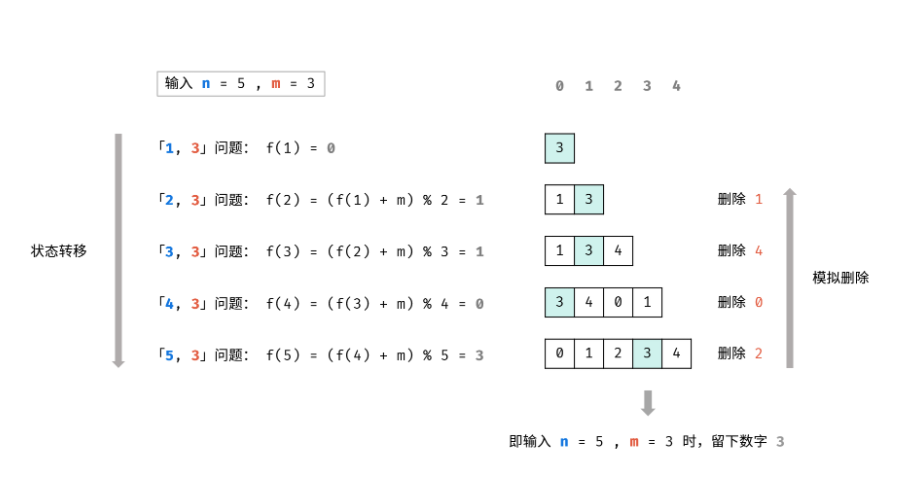
约瑟夫问题问题描述一堆人围城环。每次淘汰第m个人。最终剩下谁。 问题分析算法设计我们将上述问题建模为函数 f(n, m)，该函数的返回值为最终留下的元素的序号。 首先，长度为 n 的序列会先删除第 m % n 个元素，然后剩下一个长度为 n - 1 的序列。那么，我们可以递归地求解 f(n - 1, m)，就可以知道对于剩下的 n - 1 个元素，最终会留下第几个元素，我们设答案为 x = f(n - 1, m)。 由于我们删除了第 m % n 个元素，将序列的长度变为 n - 1。当我们知道了 f(n - 1, m) 对应的答案 x 之后，我们也就可以知道，长度为 n 的序列最后一个删除的元素，应当是从 m % n 开始数的第 x 个元素。因此有 f(n, m) = (m % n + x) % n = (m + x) % n。 算法分析算法实现 递归 12345678910111213class Solution { int f(int n, int m) { if (n == 1) { ...

元素唯一性1 元素唯一性-暴力法问题描述检验数组中元素的惟一性 算法原理暴力法 1234567UniqueElements(A[1,…n])//输出：如果A之元素全部惟一，返回“true”, 否则返回 “false”for i←1 to n-1 do for j← i+1 to n do if A[i]=A[j] return falsereturn true 算法效率n(n-1)/2 2 元素唯一性-预排序算法原理123456789PresortElementUniqueness(A[1..n])//先对数组排序来解元素惟一性问题//输入：n个可排序元素构成的一个数组A[1..n]//输出：如果A没有相等的元素，返回“true”, 否则返回”false”对数组A排序for i← 1 to n-1 do if A[i] = A[i+1] return falsereturn true 算法效率T(n)=Tsort(n) + Tscan(n) ∈Θ (nlogn) +Θ (n) = Θ (nlogn)

Huffman算法Huffman算法问题描述 一个字符串文件，我们希望尽可能多地压缩文件，但源文件能够很容易地被重建。 用特定的比特串表示每个字符，称为字符的编码，文件的大小取决于文件中的字符数n。我们可以使用一种定长编码，对每个字符赋予一个长度同为m (m≥log2n)的比特串。 设文件中的字符集是C={c1,c2,…, cn}, 又设f(ci), 1≤i≤n,是文件中字符ci的频度，即文件中ci出现的次数。 由于有些字符的频度可能远大于另外一些字符的频度，所以用变长的编码。 去除编码的二义性： 当编码在长度上变化时，我们规定一个字符的编码不能是另一个字符编码的前缀（即词头），这种码称为前缀码。 例如，如果我们把编码10和101赋予字符“a” 和“b”就会存在二义性，不清楚10究竟是“a” 的编码还是字符“b”的编码的前缀。 一旦满足前缀约束，编码即不具备二义性，可以扫描比特序列直到找到某个字符的编码。 算法原理 由Huffman算法构造的编码满足前缀约束，并且最小化压缩文件的大小。算法重复下面的过程直到C仅由一个字符组成： 设ci和cj是两个有最小...

指派问题1 指派问题-分支限界问题分析有n项任务要完成，恰好有n个人可以分别去完成其中每一项，但由于任务性质和个人专长不同，因此个人去完成不同的任务的效率（或所费时间）就有差别，由此提出下述问题：应当指派哪个人哪项任务使总的效率为最高（或花费的总时间为最小）？ 一个指派问题给出系数矩阵，或称效率矩阵，矩阵的元素cij(>0) (i, j=1, 2,…, n)表示指派第i人去完成第j向任务的效率（或时间，成本等）。解题时，我们引入0-1变量xij，令 xij=1，当指派第i人去完成第j项任务时， =0,当不指派第i人去完成第j项任务时 算法原理-匈牙利法指派问题最优解的性质：如果从系数矩阵（cij）的一行（列）各元素分别减去该行（列）的最小元素，得到新矩阵（bij） 。那么，以（bij）为系数矩阵的指派问题的最优解（xij）和原问题的最优解相同。

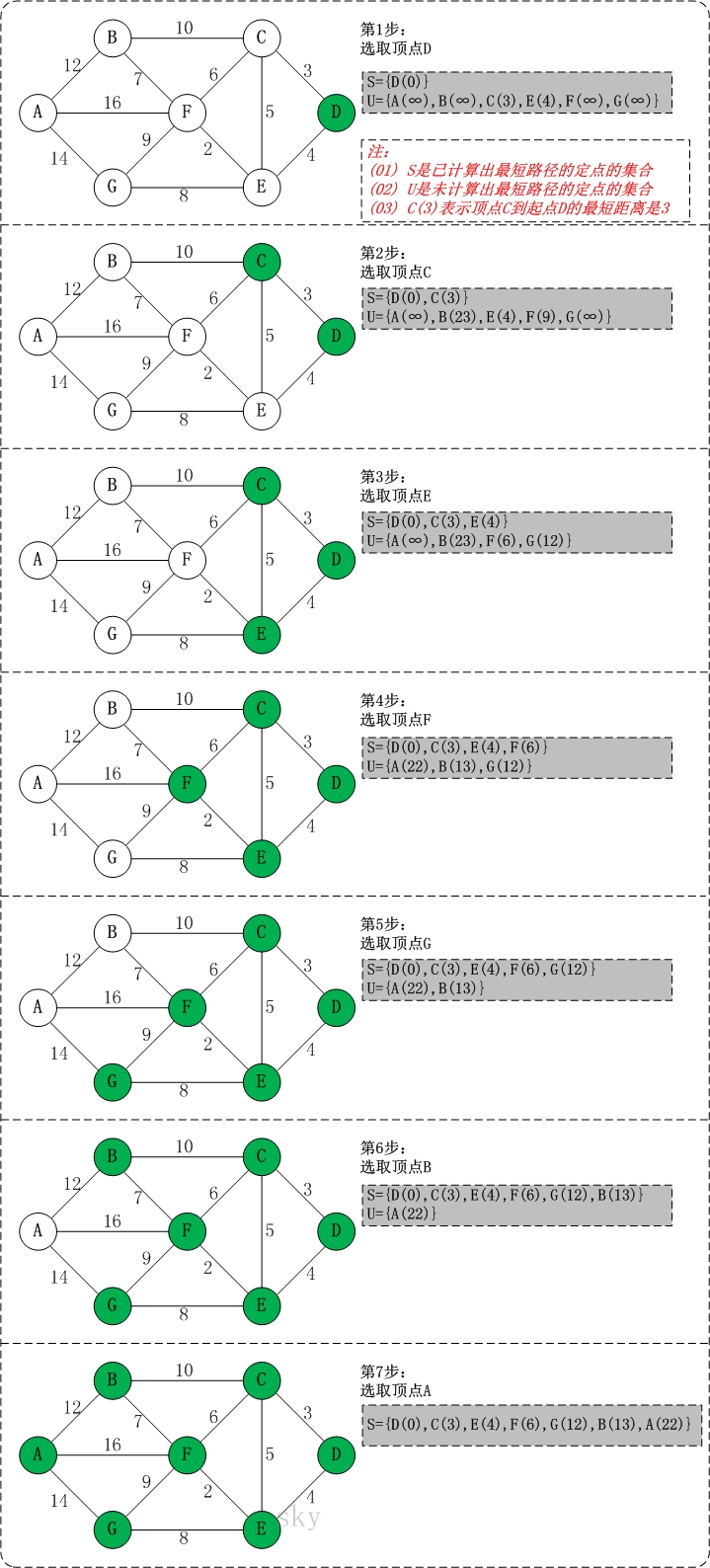
图算法-Dijkstra算法 目录 图算法-Dijkstra算法 图算法-Floyd算法 图算法-Bellman-Ford算法 图算法-Prim算法 图算法-Kruskal算法 参考文献 https://www.cnblogs.com/msymm/p/9769915.html https://blog.csdn.net/jeffleo/article/details/53349825 1 问题分析 最短路径算法。用于单源最短路算法 Dijkstra算法算是贪心思想实现的，首先把起点到所有点的距离存下来找个最短的，然后松弛一次再找出最短的，所谓的松弛操作就是，遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近，如果更近了就更新距离，这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。 2 算法原理 通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。 此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。 初始时，S...

图算法-Bellman-Ford算法 目录 图算法-Dijkstra算法 图算法-Floyd算法 图算法-Bellman-Ford算法 图算法-Prim算法 图算法-Kruskal算法 bellman ford 和 SPFA两个算法等到以后再学吧。我赌十块不需要。等到下次在复习的时候完善这两个算法，已经没时间了 参考文献 https://www.cnblogs.com/lfri/p/9521271.html https://blog.csdn.net/qq_35644234/article/details/61614581 这两个博客够了