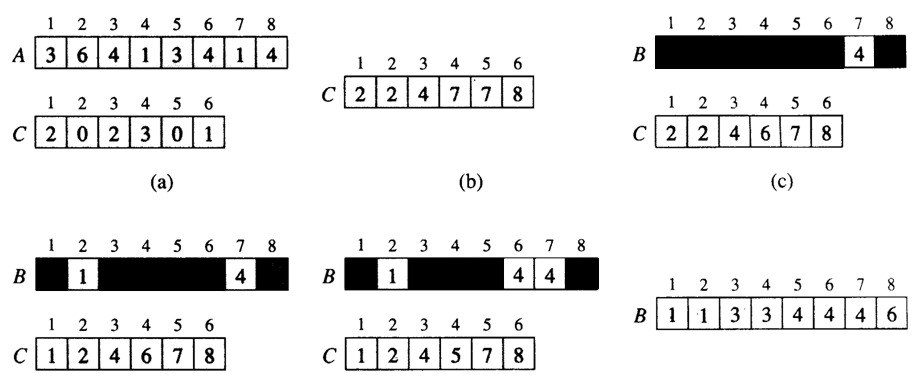
3.5 排序算法-线性排序
线性时间排序算法0 线性时间排序算法列表 线性时间排序 Name Average Worst Memory Stable Description 计数排序 (Counting Sort) n + k n + k n + k Stable Indexes using key values. 基数排序 (Radix Sort) n * k n * k n + k Stable Examines individual bits of keys. 桶排序 (Bucket Sort) n + k n2 n * k Stable Examine bits of keys. 特点给定含 n 个元素的输入序列,任何比较排序在最坏情况下都需要 Ω(n log n) 次比较来进行排序。合并排序和堆排序在最坏情况下达到上界 O(n log n),它们都是渐进最优的排序算法,快速排序在平均情况下达到上界 O(n log n)。...
3.7 字符串算法-匹配算法
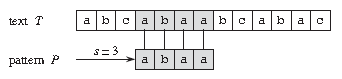
字符串匹配算法问题分析字符串匹配问题的形式定义 文本(Text)是一个长度为 n 的数组 T[1..n]; 模式(Pattern)是一个长度为 m 且 m≤n 的数组 P[1..m]; T 和 P 中的元素都属于有限的字母表 Σ 表; 如果 0≤s≤n-m,并且 T[s+1..s+m] = P[1..m],即对 1≤j≤m,有 T[s+j] = P[j],则说模式 P 在文本 T 中出现且位移为 s,且称 s 是一个有效位移(Valid Shift)。 比如上图中,目标是找出所有在文本 T = abcabaabcabac 中模式 P = abaa 的所有出现。该模式在此文本中仅出现一次,即在位移 s = 3 处,位移 s = 3 是有效位移。 解决字符串匹配的算法包括 朴素算法(Naive Algorithm) Rabin-Karp 算法 有限自动机算法(Finite Automation) Knuth-Morris-Pratt 算法(即 KMP Algorithm) Boyer-Moore 算法、Simon 算...
3.8 字符串算法-其他算法
等到以后再处理。
4.1 排列组合问题
排列问题1 排列问题-分治法、递归法问题描述R是由n个元素构成的序列集合,R={r1, r2, … ,rn},求R的全排列perm(R)。 问题分析 若R中只有1个元素{r},则perm(R)=(r) 若R中只有2个元素{r1, r2},则 perm(R)=(r1)perm(R1)∪(r2)perm(R2) 其中,Ri=R-{ri} 若R中有3个元素{ r1, r2, r3},则 perm(R)=(r1)perm(R1)∪(r2)perm(R2)∪(r3)perm(R3) 策略选择 算法思想:分治法 算法设计 划分:依次将待排列的数组的后n-1个元素与第一个元素交换。 解决:则每次递归处理的都是后n-1个元素的全排列。 合并:当数组元素仅有一个时为此递归算法的出口。即开始合并。 123456789101112算法 perm(Type list[], int k, int m)//生成列表list的全排列//输入:一个全排列元素列表list[0..n-1]//输出:list的全排列集合if k == m for i←...
5.2 凸n边形最优三角剖分问题
凸多边形最优三角剖分凸多边形最优三角剖分-动态规划问题描述给定凸多边形P={v0,v1,… ,vn-1},以及定义在由凸多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分,使得该三角剖分所对应的权,即三角剖分中诸三角形上权之和为最小。 问题分析 若凸(n+1)边形P={v0,v1,…,vn}的最优三角剖分T包含三角形v0vkvn,1≤k≤n-1,则T的权为3个部分权的和:三角形v0vkvn的权,子多边形{v0,v1,…,vk}和{vk,vk+1,…,vn}的权之和 由T所确定的这2个子多边形的三角剖分也是最优的。 因为若有{v0,v1,…,vk}或{vk,vk+1,…,vn}的更小权的三角剖分将导致T不是最优三角剖分的矛盾。 算法原理定义$t[i][j],1≤i<j≤n$为凸子多边形{vi-1,vi,…,vj}的最优三角剖分所对应的权函数值,即其最优值。 为方便起见,设退化的多边形{vi-1,vi}具有权值0。据此定义,要计算的凸(n+1)边形P的最优权值为t[1][n]。 t[i][j]的值可以利用最优子结构性质递归地计算。当j-i...
7.2 旅行商问题
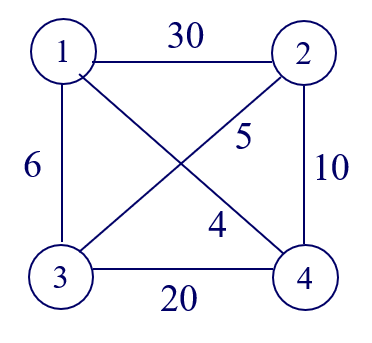
旅行商问题1 旅行商问题-回溯法问题描述某售货员要到若干城市去推销商品,已知各城市间的路程耗费(代价),如何选定一条从驻地出发,经过每个城市一遍,最后回到驻地的路线,使得总路程耗费最小。 问题分析 解向量为<i1=1,i2,i3,…,in>,其中i2,i3,…,in为{2,3,…,n}的一个排列。搜索空间为排列树 显约束: i=n时,检查是否存在一条从顶点x[n-1]到x[n]的边和一条从顶点x[n]到顶点1的边,若存在,需要判断当前回路代价是否优于已找到的当前最优回路代价bestc,若为真,更新当前最优值bestc和最优解bestx。 当i<n时,当前扩展结点位于排列树的第i-1层。若图中存在从顶点x[i-1]到顶点x[i]的边,且x[1:i]的代价小于当前最优值bestc时,进入排列树的第i层,否则剪去相应子树。 算法时间复杂度算法backtrack在最坏情况下可能需要更新当前最优解O((n-1)!)次,每次更新bestx需计算时间O(n),从而整个算法的计算时间复杂性为O(n!)。 算法原理 算法实现1234567891011...
7.1 N皇后问题
N皇后问题1 N皇后问题-回溯法问题描述在N×N的棋盘中放置N个皇后,使得任何两个皇后之间不能相互攻击,试给出所有的放置方法。 问题分析 问题解向量:(x1, x2, … , xn) 显约束:xi=1,2, … ,n 隐约束: 不同列:xi不等于xj; 不处于同一正、反对角线:|i-j|不等于|xi-xj| 算法时间复杂度(1)搜索1+n+n2+…+nn=(nn+1-1)/n-1≤2nn;(2)每个节点判断是否符合规则,最多要判断3n个位置(列方向、主与副对角线方向是否有皇后)故最坏情况下时间复杂度O(3n×2nn)=O(nn+1) 算法实现123456789101112131415bool Queen::Place(int k) { for (int j=1;j<k;j++) if ((abs(k-j)==abs(x[j]-x[k]))||(x[j]==x[k])) return false; return true;} void Queen::Backtr...
7.3 01背包问题
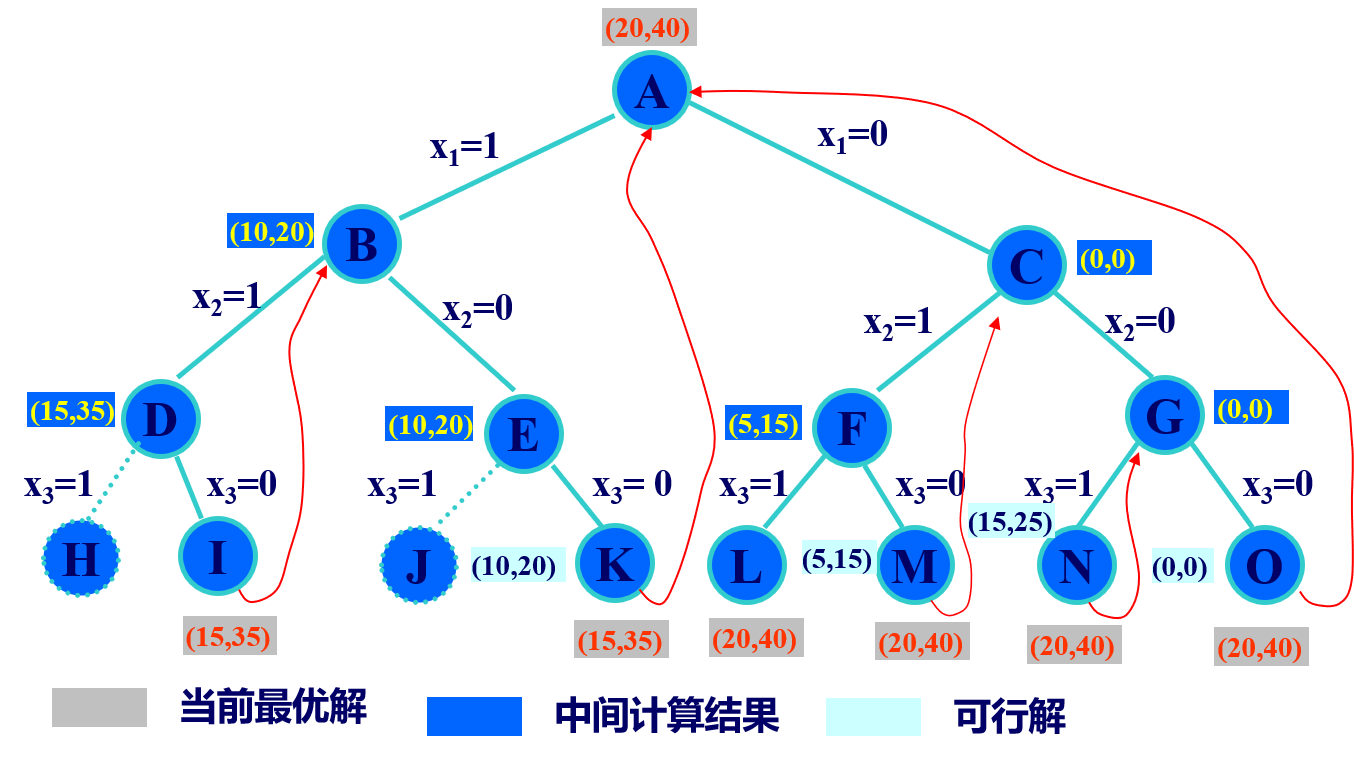
01背包问题1 01背包问题-回溯法问题描述将物品放到背包中。 n件物品 每件物品的重量为w[i] 价值为v[i] m个背包 每个背包的容量为c[j] 求背包装载的最大价值。或者是否能装下所有。 具体问题n=3,C=20,(v1,v2,v3)=(20,15,25), (w1,w2,w3)=(10,5,15),求X=(x1,x2,x3)使背包价值最大? 问题分析 解空间是子集树 可行性约束函数(剪枝函数)$\sum w_ix_i\leq c_i$ 算法原理 算法实现123456789101112131415template<class Typew, class Typep>Typep Knap<Typew, Typep>::Bound(int i){// 计算上界 Typew cleft = c - cw; // 剩余容量 Typep b = cp; // 以物品单位重量价值递减序装入物品 while (i <= n && w[i] <= cle...
7.4 作业调度问题
作业调度问题1 作业调度问题-回溯法问题描述给定n个作业的集合{J1,J2,…,Jn}。每个作业必须先由机器1处理,然后由机器2处理。作业Ji需要机器j的处理时间为tji。对于一个确定的作业调度,设Fji是作业i在机器j上完成处理的时间。所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和。 批处理作业调度问题要求对于给定的n个作业,制定最佳作业调度方案,使其完成时间和达到最小。 问题分析 解空间:排列树问题。
7.5 完全背包问题
完全背包问题1 完全背包问题将物品放到背包中。 无限件物品 每件物品的重量为w[i] 价值为v[i] m个背包 每个背包的容量为c[j] 求背包装载的的最大价值。