Estom的博客

矩阵的初等变换1 矩阵的初等变换初等变换的定义矩阵的初等行变换$A\sim^r B$、初等列变换$A\sim^c B$ 对调两行 数乘某一行 某一行元素的k倍加到另外一行 初等行变换与初等列变换统称初等变换。记作$A\sim B$ 初等变换的性质 反身性$A \sim A$ 对称性$A\sim B,B\sim A$ 传递性$A\sim B,B\sim C,A\sim C$ 初等变换的形式 行阶梯形式：阶梯型。 行最简形式：每一行第一个非零元素为1，且该列其他元素为零。 标准形式：行变换后，进行列变换，到达行最简形式，列最简形式。左上角单位阵$$F=\begin{bmatrix} E_r & 0\ 0 & 0\end{bmatrix}_{m\times n}$$ 初等变换的乘积表示 $A\sim^r B$的充要条件存在m阶可逆矩阵P，使$PA = B$ $A\sim^c B$的充要条件存在n阶可逆矩阵Q，使$AQ = B$ $A\sim B$的充要条件存在m阶可逆矩阵P，存在n阶可逆矩阵Q，使$PAQ =B$ ...

向量7 向量运算定义：向量内积$$x=(x_1,\cdots,x_n)^T\y=(y_1,\cdots,y_n)^T\[x,y]=x^Ty=x_1y_1+\cdots+x_ny_n$$[x,y]称为向量的内积。 性质：向量内积 $[x,y]=[y,x]$ $\lambda[x,y]=[\lambda x,y]$ $[x+y,z]=[x,z]+[y,z]$ $x=\overrightarrow{0},=>[x,x]=0\x \not =\overrightarrow{0},=>[x,x]\not =0$ 施瓦茨不等式：$[x,y]^2\geq [x,x]+[y,y]$ 定义：向量长度（范数）$$||x||=\sqrt{[x,x]}=\sqrt{x_1^2+\cdots+x_n^2}$$ 性质：向量长度 非负性：$x=\overrightarrow{0},=>||x||=0\x \not...

矩阵相似变换1 特征值和特征向量 应用，方阵的对角化，解微分方程 定义：特征值和特征向量 声明 $$A是n阶矩阵\\lambda 数\x是n维向量$$ 条件特征表达式$$Ax=\lambda x$$ 结论$$\lambda 是矩阵A的特征值\x是矩阵A的特征向量。$$ 性质：特征值特征向量 同一个特征值的所有特征向量的非零线性组合，仍是特征向量。 特征值的性质：$$\lambda_1+\cdots+\lambda_n=a_1+\cdots+a_n\\lambda_1\cdots\lambda_n=|A|=det A$$ 定理：特征值、特征向量、矩阵的线性变换$$\lambda 是矩阵A的特征值，p是属于lambda的特征向量$$ $k\lambda 是kA的特征值，p是kA属于k\lambda的特征向量$ $\lambda^k是A^k的特征值，p是A^k属于\lambda^k的特征向量$ $\frac{1}{\lambda}是A^{-1}的特征值$ $\varphi(A)是A的m次多项式，\varphi(\lambda)是\va...

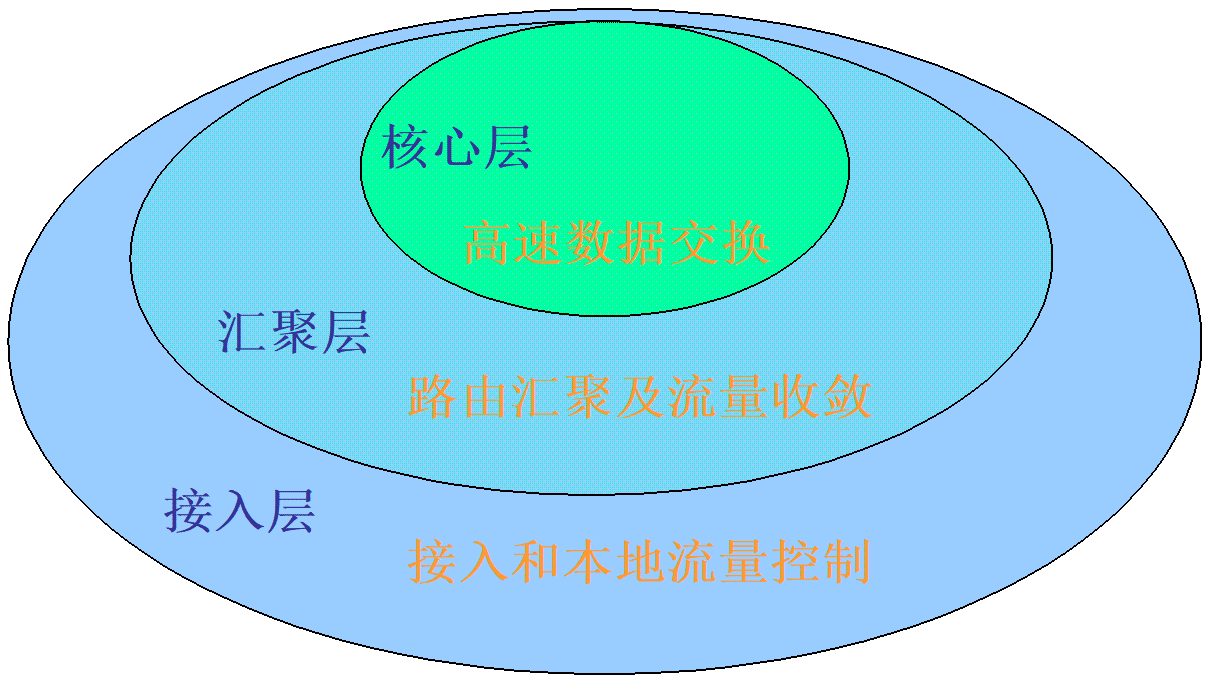
e# 综合组网试验 1 总体规划设计系统需求和设计目标6层楼约30个机房约1600多台计算机，为一般网络应用、监控、服务器、存储、信息发布、电子教室、中控和投影等多个系统提供网络平台 将整个实验中心机房连成一个相对独立的局域网，保证互联互通、学生自由上机、正常上网、刷卡系统、网络服务器、考试系统的正常运行。 满足多媒体教学、流媒体教学的需要，保证音、视频的流畅播放，确保良好的服务质量。 网络的连通性完全可控，要求满足某些机房考试时禁止该机房访问互联网，而其他机房正常上课不受影响。 网络支持组播应用，能够满足机房管理软件等教学相关应用的需求。 网络设备支持抗ARP病毒攻击、广播风暴抑制、DHCP协议、IPv6协议等功能。 所有网络设备都要能够被实时监控和管理。 总体规划 信息平台网络采用TCP/IP体系结构，以满足与其他网络系统的互联互通。 分层次的方法划分网络 不同层次使用不同级别的千兆交换机，出口路由器采用中高端路由器 采用地址转换技术(NAT)规划网络。IP地址的划分采用每个机房一个网段。NAT采用基于端口的NAT-PT技术。申请至少128个公网地址的地址池。 ...

综合组网实验1 网络需求分析任务 网络建设目标分析 网络应用约束分析 网络技术分析 网络规格参数分析等 手段 了解应用背景 查询技术文档 与客户交流 2 网络规划设计指标的分析和评估 网络的规模 网络的结构 网络管理 网络的扩展 网络安全 外部网络的互联 分许报告 网络的规模 该方案的优点 现有网络状况 网络的运行方式 安全性要求 网络可提供的应用 响应时间 可靠性 节点的分布 扩展性 3 网络系统设计内容 网络系统需求：对网络需求进行分类 网络体系结构的设计：传输方式、客户接口、服务器、网络划分、互联设备。使用体系结构图表示结果。 网络拓扑结构设计：综合性、高可靠性、高性能、层次性、支持qos、安全性、扩展性、开放性、标准化、实用性。 网络安全性设计；网络层安全、系统安全、客户安全、应用程序安全、数据安全。 4 网络设备选型主要设备工作站、服务器、路由器、交换机/集线器、共享设备、网络适配器、加密设备、 UPS电源 选取原则 采用的网络技术 支持的网络应用 设备在网络中的功能和所处位置 5 系统集成 系统逻辑结构图的设计 项目及分包商的管理 硬件和软件产...

单元最短路问题 通过不同的方式解决单元最短路问题 图，不是树 0 问题描述单元最短路问题、有向无环图 1 暴力求解深度优先搜索DFS广度优先搜索BFS2 回溯法深度优先算法，每次回溯的时候进行剪枝操作。如果此分支没有希望比已经保存的最短路更优。 而且可以从不同的点到达同一个点。保留之前到达这个点的状态，如果最新到达这个点的距离小于之前的距离，则继续向下走，如果大于则放弃并回溯。

正太总体参数的假设检验 一会单独复习这里 1 单个总体-方差已知-均值检验假设检验类型$$\begin{aligned}H_0:\mu=\mu_0,& H_1:\mu>\mu_0\H_0:\mu\leq\mu_0,&H_1:\mu>\mu_0\H_0:\mu=\mu_0,&H_1:\mu<\mu_0\H_0:\mu\geq\mu_0,&H_1:\mu<\mu_0\end{aligned}$$ 假设检验-z检验步骤 关于假设检验，需要使用样本统计量和临界值对应样本空间的接受域和拒绝域。 命题假设$H_0:\mu\in\Theta_0,H_1:\mu\in\Theta_1$ 检验统计量$z=\frac{\overline{x}-\mu_0}{\sigma/\sqrt{n}}$ 根据检验水平计算拒绝域的临界值$\双侧检验W={(x_1,\dotsm,x_n:|z|\geq z_{1-\frac{\alpha}{2}}}\单侧检验W&#x...

Pearson检验1 总体分布的$\chi^2$拟合检验定理：Pearson定理 条件$$样本容量n充分（n>=50),无论总体服从何种分布F_0(x)\\chi^2=\sum_{i=1}^k\frac{(f_i-np_i)^2}{np_i}\$$ 结论$$统计量\chi^2服从自由度为k-1的\chi^2分布$$ 步骤 把实轴$(-\infin,+\infin)$分成k个互不相交的区间$A_i=(a_i,a_{i+1}],i=1,2,\dotsm,k$，其中$a_1,a_{k+1}$分别取$-\infin,+\infin$。区间划分视具体情况而定。 计算概率。计算$np_i$称为理论频数$$p_i = P{X\in A}=F_0(a_{i+1})-F_0(a_i),i=1,2,\dotsm,k\$$ 计算样本观察值$x_1,\dotsm,x_n$落在区间$A_i$上的个数$f_i$，称为实际频数。 通过计算公式计算$\chi^2$的值 对于给定的显著性水平$\alpha$可得临界值$\chi...

WPS 配置wps官网下载 字体放到/usr/share/fonts/ Sogou拼音配置Vscode配置