数据结构
文章
7 图
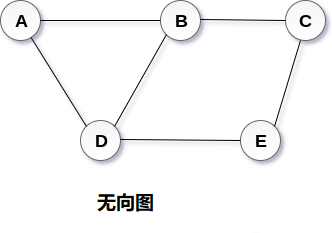
图1 简介概念 图可以定义为用于顶点和边的组合。 图可以看作是循环树,图中顶点(节点)维持它们之间的任何复杂关系,而不是简单的父子关系。 图G 可以定义为有序集G(V,E),其中V(G)表示顶点集,E(G)表示用于连接这些顶点的边集。 图G(V,E)有5个顶点(A,B,C,D,E)和6个边((A,B),(B,C),(C,E),(E,D), (D,B),(D,A))如下图所示。 术语 阶(Order) - 图 G 中点集 V 的大小称作图 G 的阶。 子图(Sub-Graph) - 当图 G’=(V’,E’)其中 V‘包含于 V,E’包含于 E,则 G’称作图 G=(V,E)的子图。每个图都是本身的子图。 生成子图(Spanning Sub-Graph) - 指满足条件 V(G’) = V(G)的 G 的子图 G’。 导出子图(Induced Subgraph) - 以图 G 的顶点集 V 的非空子集V1 为顶点集,以两端点均在 V1 中的全体边为边集的 G 的子图,称为 V1 导出的导出子图;以图 G 的边集 E 的非空子集 E1 为边集,以 E...
8 跳表
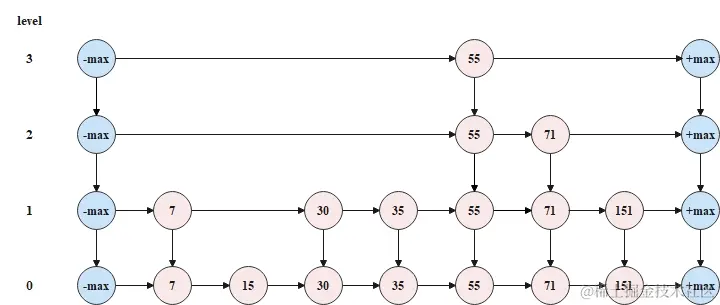
跳表跳表的基本概念 经典实现:Redis 的 Sorted Set、JDK 的 ConcurrentSkipListMap 和 ConcurrentSkipListSet 都是基于跳表实现。 只需要对链表稍加改造,就可以支持类似“二分”的查找算法。我们把改造之后的数据结构叫作跳表(Skip list)。 跳表是一种各方面性能都比较优秀的动态数据结构,可以支持快速的插入、删除、查找操作,写起来也不复杂,甚至可以替代红黑树(Red-black tree)。 在一个单链表中查询某个数据的时间复杂度是 O(n)。 在一个具有多级索引的跳表中,第一级索引的结点个数大约就是 n/2,第二级索引的结点个数大约就是 n/4,第三级索引的结点个数大约就是 n/8,依次类推,也就是说,第 k 级索引的结点个数是第 k-1 级索引的结点个数的 1/2,那第 k 级索引结点的个数就是 $n/(2^k)$ 跳表的原理跳表的结构 跳表的特点,可以概括如下。根据以下原则构建跳表。 跳表是多层(level)链表结构;跳表中的每一层都是一个有序链表,并且按照...